What Is a Circle?
A circle is a round-shaped figure that has no corners or edges.
In geometry, a circle can be defined as a closed shape, two-dimensional shape, curved shape.

A few things around us that are circular in shape are a car tire, a wall clock that tells time, and a lollipop.

Recommended Games
Center of a Circle
The center of a circle is the center point in a circle from which all the distances to the points on the circle are equal. This distance is called the radius of the circle.
Here, point P is the center of the circle.
Recommended Worksheets
Interior and Exterior of a Circle
Consider the circle with center P and radius r. A circle has an interior and an exterior region.
All those points for which the distance is less than the radius of a circle lie in the interior of the circle. For example points P, Q, and R lie in the interior of the circle.
All those points for which the distance is greater than the radius of a circle lie in the exterior of the circle. For example points S and T lie on the exterior of the circle.
All those points for which the distance is equal to that of the radius of a circle lie on the circle. For example points U and V lie on the circle.
Semicircle:
Semi means half, so semicircle is half a circle. It is formed by cutting a whole circle along a line segment passing through the center of the circle. This line segment is called the diameter of the circle.
Quarter Circle:
Quarter means one-fourth. So, a quarter circle is a quarter of a circle, formed by splitting a circle into 4 equal parts or a semicircle into 2 equal parts.
A quarter circle is also called a quadrant.
Parts of a Circle
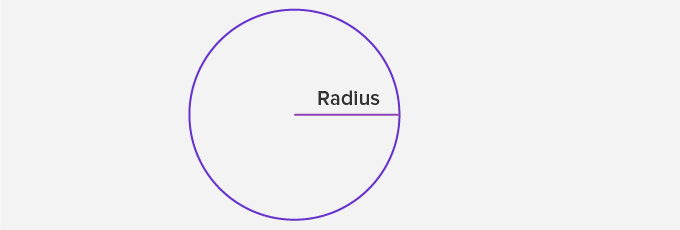
The Radius of a Circle:
A radius is a line segment with one endpoint at the center of the circle and the other endpoint on the circle.
Radius = $\frac{Diameter}{2}$
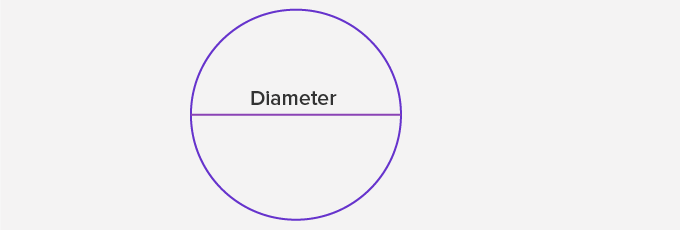
Diameter of a Circle:
A line segment passing through the center of a circle, and having its endpoints on the circle, is called the diameter of the circle.
Diameter = 2 × radius
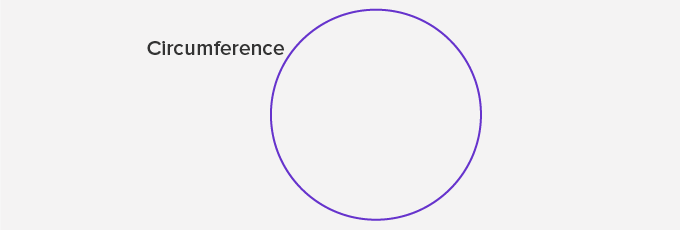
Circumference:
The circumference of a circle is the distance around a circle. It is the same as the perimeter of other shapes.
Chords of Circles:
A line segment with its endpoints lying on a circle is called the chord of the circle.
The diameter of a circle is its largest chord.
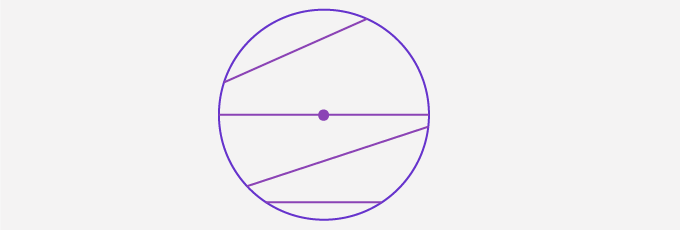
Arc of a Circle:
An arc is a part of the circle, with all its points on the circle. It is a curve that is a part of its circumference.
An arc that connects the endpoints of the diameter has a measure of 180° and it is called a semicircle.
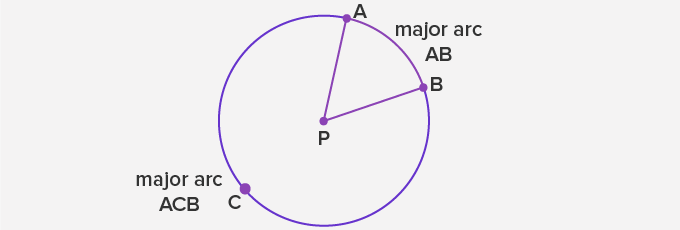
An arc divides the circle into two parts. The smaller part is called the minor arc and the greater part is called the major arc.
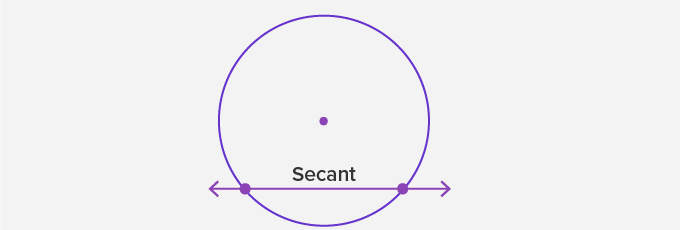
The Secant of a Circle:
A secant is a line that intersects a circle at exactly two points.
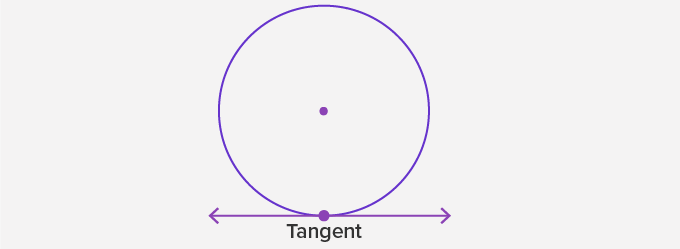
Tangent of a Circle:
A tangent is a line that intersects a circle at exactly one point.
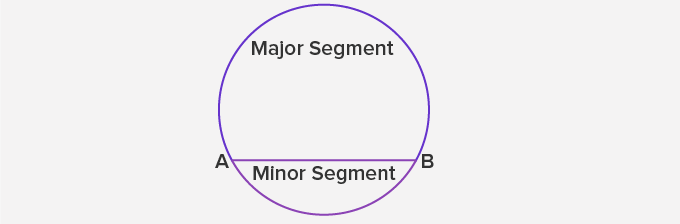
Segments of a Circle:
A chord of a circle divides the circular region into two parts. Each part is called the segment of the circle.
The segment containing the minor arc is called the minor segment and the segment containing the major arc is called the major segment.
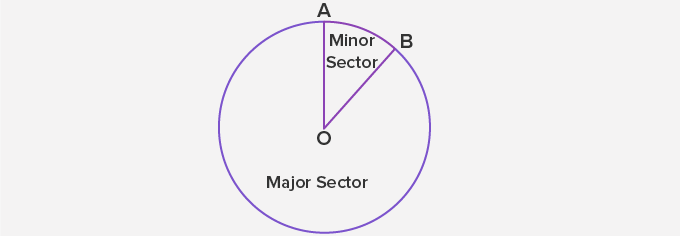
The Sector of a Circle:
The sector of a circle is a part of the circle that is enclosed by two radii and an arc of the circle as a part of its boundary.
When two radii meet at the center of the circle to form the sector, it actually forms two sectors. A sector of a circle is called the minor sector if the minor arc of the circle is a part of its boundary. A sector is called the major sector if the major arc of the circle is a part of its boundary.
Circle Formulas
Area of a circle:
The area of a circle is the region enclosed inside the circle.
The area of a circle depends on the length of its radius.
Area = $\pi$r$^{2}$
Circumference:
The distance around the circle is the circumference of the circle.
Circumference = 2$\pi$r
The value of $\pi$ = 3.14 or $\frac{22}{7}$
Solved Examples on Circle
Example 1: Match each term with the correct definition.

Solution:
1 – b
2 – d
3 – a
4 – c
Example 2: Use the figure to answer the questions.
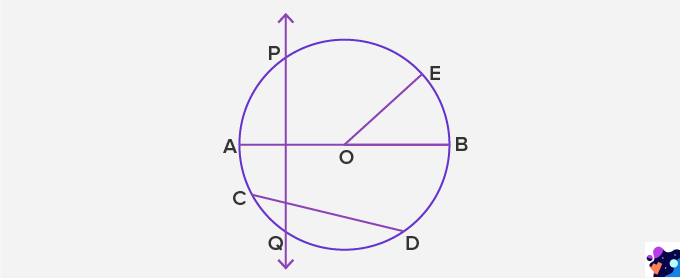
- Which term best describes OE?
- Name 3 line segments that have the same length.
- Name the secant.
- Which two terms can be used to describe AB?
Solution:
- Radius
- OA, OB, and OE
- PQ
- Diameter and chord
Example 3: If a circle has a radius of 3 cm, what is the length of its longest chord?
Solution:
The longest chord is the diameter of the circle.
Diameter = 2 × radius = 2 × 3 = 6 cm
Example 4: The minute hand of a circular clock is 21 cm long. How far does the tip move in 1 hour?
Solution:
The distance covered in 1 hour is the circumference of the clock, which is a circle.
Circumference = 2$\pi$r = 2 × $\frac{22}{7}$ × 21 = 132 cm
Practice Problems On Circle
Circle
A circle with center O has radius 5 cm and OQ = 7 cm, then where does point Q lie?
The length of OQ is greater than the radius of the circle. So point Q lies in the exterior of the circle.
The total number of diameters of a circle is:
Diameter is the line segment passing through the center of the circle and having endpoints on the circle. There are infinite lines that can pass through a point and so there is an infinite number of diameters of a circle.
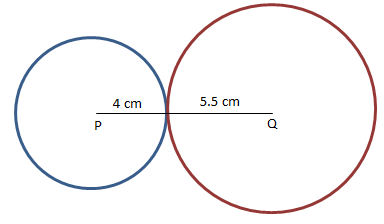
Two circles of center P and Q with radii 4 cm and 5.5 cm touches externally, what is the distance between their centers?
The distance between centers = 4 cm + 5.5 cm = 9.5 cm
If the circumference of the circle is 176 cm. What will be its area?
Circumference = 2πr
176 = 2 × $\frac{22}{7}$ × r
r = 28 cm
Area = πr2 = $\frac{22}{7}$ × 28 × 28 = 2,464 cm2
Frequently Asked Questions On Circle
How many circles can be drawn to pass through two given points?
Only one circle can be drawn passing through two given points.
The diameter of a circle divides the circular region into how many parts?
Two equal parts, each part is called a semicircular region.
What are the major parts of a circle?
The different parts of a circle are radius, diameter, chord, secant, tangent, minor arc, major arc, minor segment, major segment, minor sector, and major sector.
What is the perimeter of a circle?
c = 2$\pi$r, where c is the circumference and r is the radius.
What are concentric circles?
Concentric circles are circles having the same center.