What is a Perimeter?
In geometry, the perimeter of a shape is defined as the total length of its boundary. The perimeter of a shape is determined by adding the length of all the sides and edges enclosing the shape. It is measured in linear units of measurement like centimeters, meters, inches, or feet.
Let’s try to calculate the perimeter of the following shape:
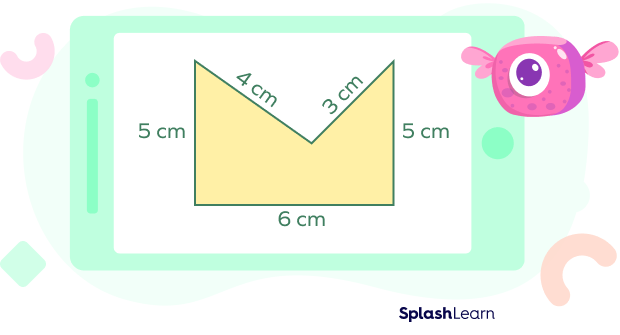
Perimeter of a shape = Sum of all its sides,
Therefore,
Perimeter of the given shape = 6 cm + 5 cm + 5 cm + 4 cm + 3 cm = 23 cm.
Recommended Games
How to Find Perimeter
Perimeter of a Regular Shape
We know that the length of each side of a regular polygon is the same.
Therefore,
Perimeter of regular polygon = sum of all its sides = number of sides ✕ length of one side.
For example, look at the given regular pentagon.
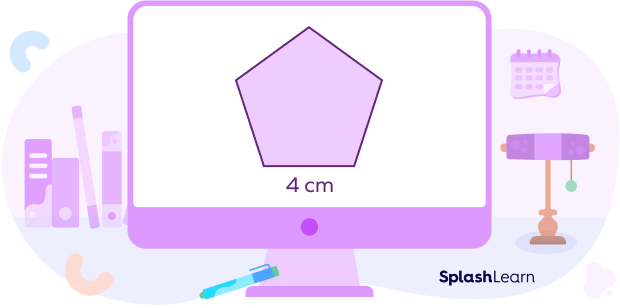
The perimeter of the given regular pentagon can be calculated as follows:
Number of sides = 5
Length of one side = 4 cm
Therefore, Perimeter = number of sides ✕ length of one side
= 5 ✕ 4 = 20 cm
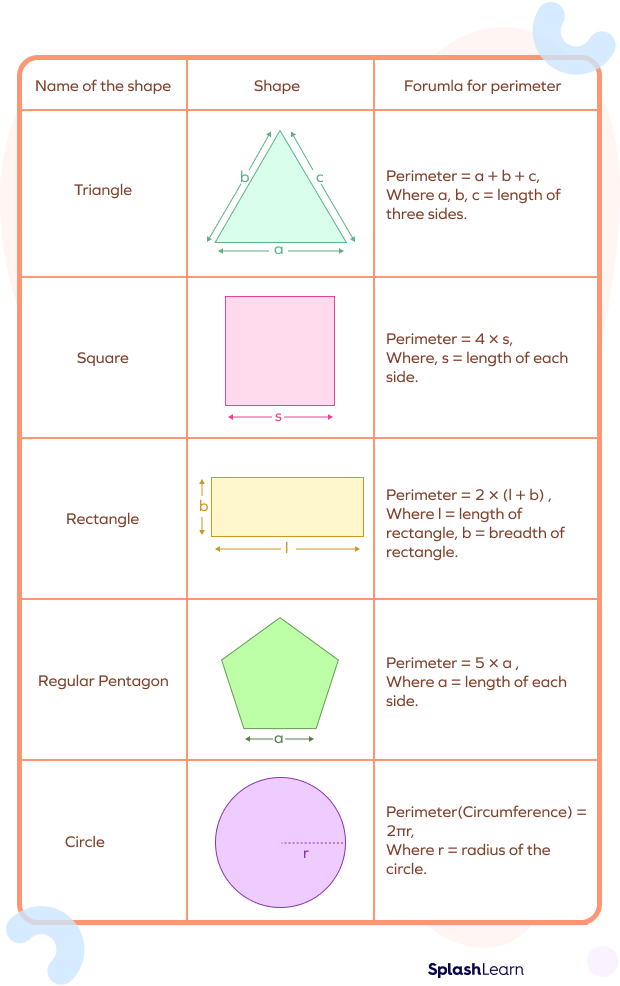
The given table summarizes the formulas to find the perimeter of some regular polygons:
Perimeter of An Irregular Shape
Since the sides of an irregular polygon may not all be the same in length, we use the general formula to find the perimeter of an irregular shape.
Therefore,
Perimeter of irregular polygon = sum of all sides.
Real – World Applications
We often use the concept of perimeter in real life. For example, when putting up Christmas lights around the house or when we want to put a fence around the backyard, we find its perimeter to know the length of wire we will need.

Solved Examples On Perimeter
Example 1: What is the perimeter of the given figure?
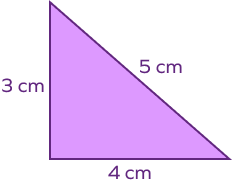
Solution:
We know that the perimeter of a triangle is given by
Perimeter = a + b + c,
Where a, b, c = length of three sides.
Therefore,
For the given triangle,
Perimeter = 5 cm + 4 cm + 3 cm = 12 cm
Example 2: Calculate the perimeter of the following figure.
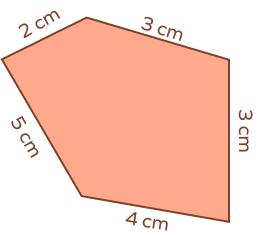
Solution:
The given shape is an irregular pentagon.
The perimeter of this pentagon will be given by the sum of all its sides.
Perimeter = 2 cm + 3 cm + 3 cm + 4 cm + 5 cm = 17 cm
Example 3: What will be the perimeter of a rectangle with length 12 cm and breadth 5 cm?
Solution:
We know that the perimeter of a rectangle is given by
Perimeter = 2 ✕ (l + b),
Where l = length of the given rectangle, b = breadth of the given rectangle.
For the given rectangle, l = 12 cm, b = 5 cm.
Therefore, perimeter of given rectangle = 2 ✕ (12 + 5) = 2 ✕ 17 = 34 cm
Practice Problems On Perimeter
Perimeter
Find the perimeter of a square that has sides of 40 cm in length each.
Perimeter of the given square = 4 ✕ 40 = 160 cm
Calculate the perimeter of a rectangle with length = 30 cm and breadth = 14 cm.
Perimeter of the given rectangle = 2 ✕ (30 + 14) = 2 ✕ 44 = 88 cm
Find the perimeter of a circle with radius = 7 cm.
Perimeter of given circle = 2 ✕ 3.14 ✕ 7 = 43.96 cm
Calculate the perimeter of the following figure:
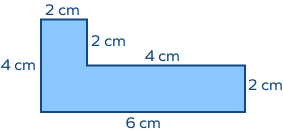
Perimeter of irregular polygon = sum of all sides
Perimeter of given irregular polygon = 6 cm + 4 cm + 2 cm + 2 cm + 4 cm + 2 cm = 20 cm
Frequently Asked Questions On Perimeter
How many sides are required to determine the perimeter of a regular heptagon?
We only require the length of one side to determine the perimeter of any geometric figure with sides of equal length, such as a regular heptagon. The area of a heptagon = 7 ✕ a, where a is the side length.
What is the difference between the perimeter and area of a 2-D shape?
Perimeter measures the length of the boundary of the shape. It is given by the sum of all sides of the shape. It is one-dimensional and expressed in linear units.
Area, on the other hand, measures the space occupied by the shape. It is two-dimensional and is expressed in square units.
How can we find the perimeter of a polygon?
The most general way to find the perimeter of any polygon is to find the sum of all its sides. However, another way of finding the perimeter of a regular polygon is to multiply the number of its sides by the side length.


























