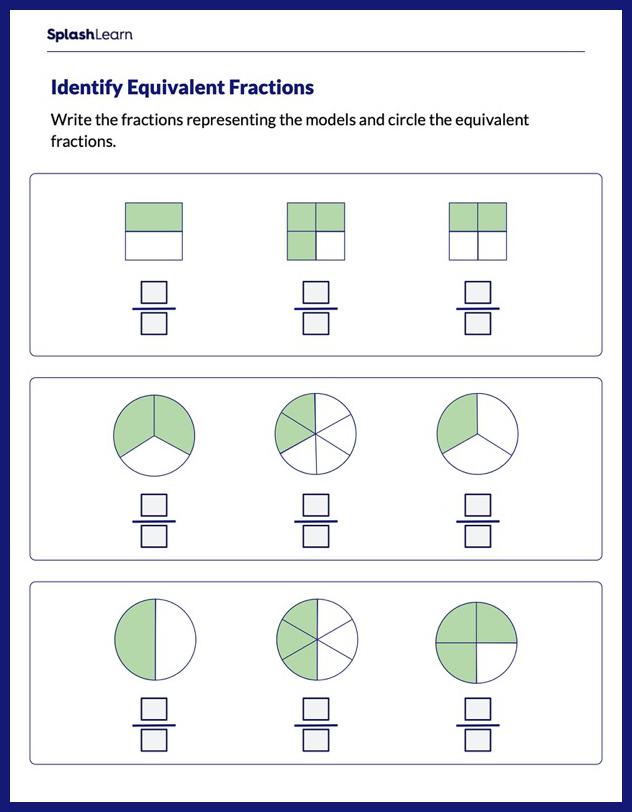
What is a Semicircle?
In geometry, a semicircle is defined as a half circle formed by cutting the circle into two halves. It is formed when a line passes through the center and touches the two ends of the circle. This line is called the diameter of the circle.
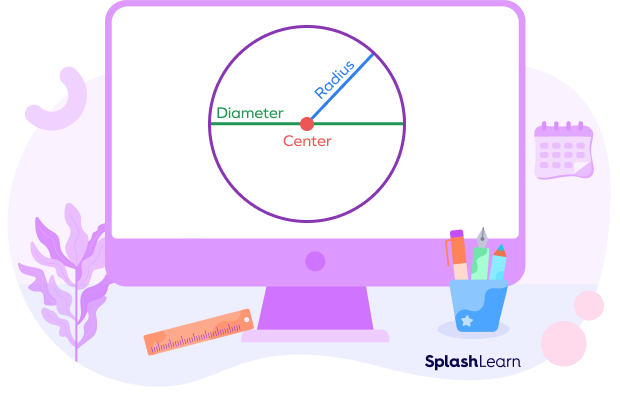
In the figure above, you can see the diameter dividing the circle into two halves.
You can also see a blue line drawn from the circle’s center to a point on its edge. The length of the line gives the radius of the circle.
All points on a circle are at an equal distance from its center. So, no matter which point you touch from the center, the radius will always be the same.
Recommended Games
Finding the Area of a Semicircle
The area of a semicircle refers to the space inside it or the region enclosed by it. It is half the area of a circle.
Recall that area of a circle is πr², where:
- r is the radius of the circle.
- π is Pi with an approximate value of 22/7 or 3.14.
So, the formula for calculating the area of a semicircle is:
Area = ½ × πr²
Recommended Worksheets
Finding the Perimeter/Circumference of a Semicircle
The perimeter or circumference describes the total length of the boundary of the semicircle.
You may think that the perimeter of a semicircle is half the perimeter of a circle, but that is not true.
Half the perimeter of a circle gives the perimeter of the curved part only. You will also have to add the diameter line across the bottom to get the total perimeter.
Recall that the perimeter of a circle is 2πr.
So, the perimeter of the curved part of the semicircle is ½ × 2πr = πr
Now, let’s add the length of the diameter as well.
So, the total perimeter of the semicircle = πr + d, where d is the diameter.
But, we also know that the diameter of a circle is twice its radius.
So, substituting the diameter with the radius in the above equation, we get,
The perimeter of semicircle = πr + 2r
Or, perimeter = r (π + 2)
Solved Examples
Example 1: A circle has a diameter of 14 cm. Find the area of the semicircle. (Use π = 22/7)
Solution:
Given: Diameter of a circle = 14 cm
Radius = Diameter/2 = 14/2 = 7 cm
Now,
Area of the semicircle = ½ × πr²
= ½ × 22/7 × 7 ×7
= 77 cm²
Example 2: A semicircle has a diameter of 28 cm. Find its perimeter. (Use π = 22/7)
Solution:
Given: Diameter of the semicircle = 28 cm
Radius = Diameter/2 = 28/2 = 14 cm
Now,
Perimeter of a semicircle = πr + 2r
= 22/7 × 14 + 2 × 14
= 44 + 28
= 72 cm
Example 3: The diameter of a semicircle is 7 cm. Find the perimeter of its curved surface. (Use π = 22/7)
Solution:
Given: The diameter of the circle is 7 cm
Radius = 7/2 cm
Now,
The perimeter of the curved surface of semicircle = ½ × 2πr
= ½ × 2 × 22/7 × 7/2
= 11 cm
Practice Problems
Semicircle - Definition With Examples
A basketball court has two semi-circles at the two ends of the court. If the semi-circles have a radius of 7 feet, find the perimeter of one of the semi-circles. (Use π = 22/7)
Given: The radius of the semi-circle is 7 feet.
Perimeter of the semi-circle $= πr + 2r$
$= 22/7 × 7 + 2 × 7$
$= 22 + 14$
$= 36$ feet
Amy made a circular cake with a diameter of 12 cm. Find the area of half of the cake. (Use π = 3.14)
Given: Diameter of the cake $= 12 cm$
So, radius $= 12/2 = 6 cm$
Area of semicircle $= ½ × πr²$
$= 1/2 × 3.14 × 6 × 6$
$= 56.52$ cm²
Harry has a circular garden with a radius of 7 yards. He wants to grow flowers in half of the garden. What is the area of the part he wants to grow flowers in? (Use π = 22/7)
Given: Radius of the garden $= 7 yards$
Area of semicircle $= ½ × πr²$
$= 1/2 × 22/7 × 7 × 7$
$= 77$ yard²
The perimeter of a semicircle is 36 units. Find its diameter. (Use $π = 22/7$)
Given: Perimeter of semicircle $= 36 units$
We know the perimeter $=$ r $(π + 2)$
or, $36 =$ r $(22/7 + 2)$
or, $36 =$ r $× 36/7$
or r $= 36 × 7/36$
Therefore, r $= 7$
Diameter $= 2 × 7 = 14$ units
Frequently Asked Questions
Are semicircles and half circles the same?
Yes, a half circle is the same as a semicircle. It is formed by cutting a circle into two equal halves.
What are the examples of objects with semicirclular shape?
Protractors, Japanese fans, tacos, and tunnels are some examples of semicircles.
How many semicircles are there in a circle?
There are two semicircles in a circle.