What is Geometry In Math?
Geometry is a branch of mathematics that studies the sizes, shapes, positions, angles, and dimensions of things.
2D Shapes in Geometry
Flat shapes like squares, circles, and triangles are a part of flat geometry and are called 2D shapes. These shapes have only 2 dimensions, the length and the width.
Examples of 2D shapes in flat geometry are as shown below.
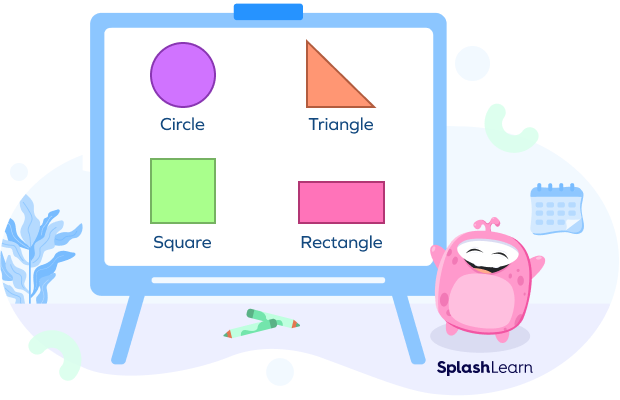
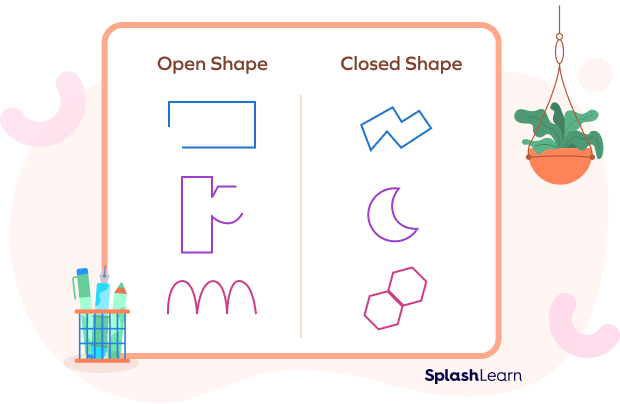
2D shapes can be further classified as open shapes and closed shapes. Open shapes can be defined as a shape or figure whose line segments and/or curves do not meet. They do not start and end at the same point. Closed shapes are geometric shapes that begin and end at the same point.
3D Shapes in Geometry
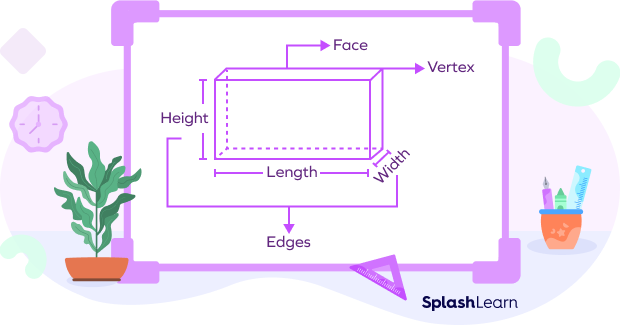
In geometry, a three-dimensional shape can be defined as a solid figure or an object or shape that has three dimensions – length, width, and height. Unlike two-dimensional shapes, three-dimensional shapes have thickness or depth.
The attributes of a three-dimensional figure are faces, edges, and vertices. The three dimensions compose the edges of a 3D geometric shape.
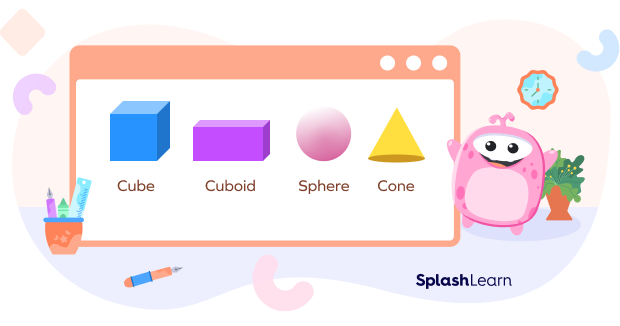
A cube, rectangular prism, sphere, cone and cylinder are the basic 3-dimensional shapes we see around us.
Angle
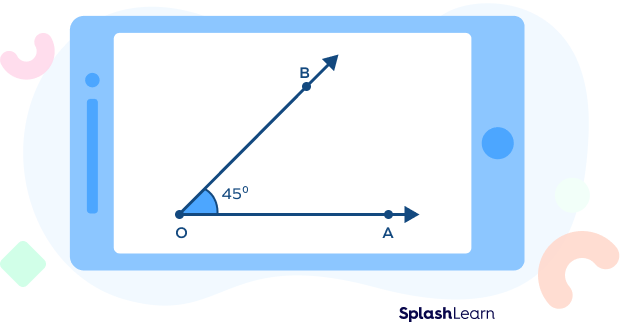
In geometry, an angle can be defined as the figure formed by two rays meeting at a common endpoint. An angle is represented by the symbol ∠. Angles are measured in degrees (°) using a protractor. For example, 45 degrees is represented as 45°.
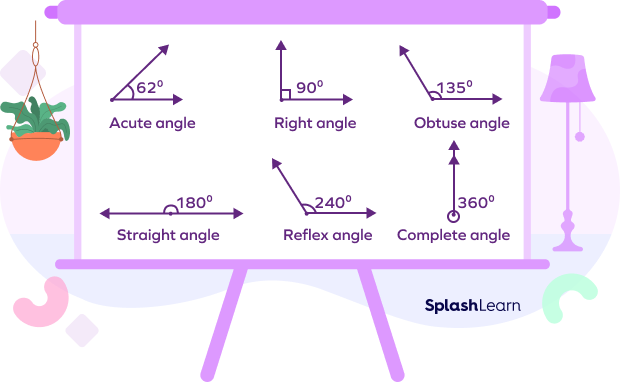
The angles are classified based on their measurements as:
- An acute angle measures less than 90°.
- An obtuse angle is between 90° and 180°.
- A right angle precisely measures 90°.
- An angle measuring exactly 180° is a straight angle.
- A reflex angle measures between 180°- 360°.
- A complete angle measures 360°.
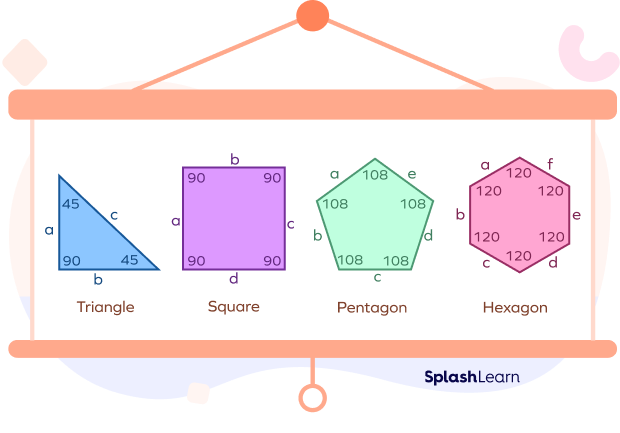
The vertex of a shape where two edges meet form an angle. Different shapes in geometry have different angle measures.
For example:
- A triangle is a 3 sided shape, and the sum of its 3 interior angles is 180˚
- A square, rectangle or quadrilateral are 4 sided shapes, and the sum of their 4 interior angles is 360˚
- Other polygons like the pentagon, hexagon, heptagon, octagon have 5, 6, 7, 8 sides respectively and varying angles.
Examples of different Polygons with their angles and sides are as shown below.
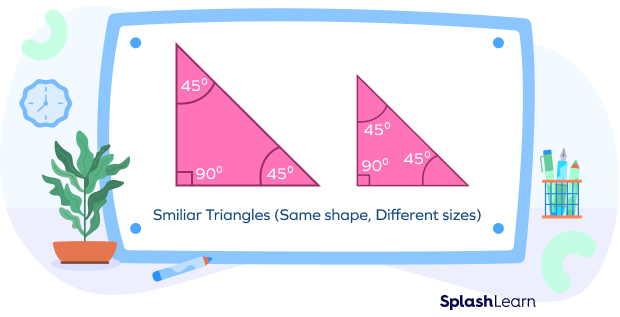
We learn various aspects of shapes, like the measurement of angles, length of sides, area, volume, etc in geometry. Similarity and congruence are two important aspects of geometry.
Similarity: Similarity is when two shapes are the same but their sizes may vary.
Congruence: Congruence is when two shapes are exactly the same in shape and size.
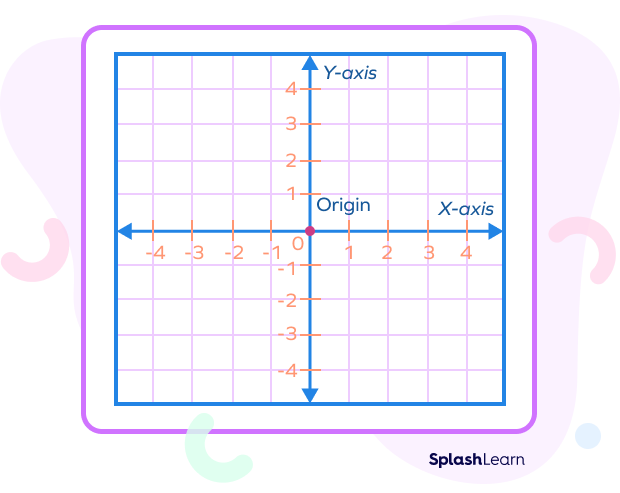
Coordinate Plane:
- A coordinate plane is a 2D surface formed by using two number lines that intersect each other at the right angle.
- The horizontal number line is the x-axis, and the vertical number line is the y-axis.
- The intersection of the two axes is the (0,0) coordinate.
- Using the coordinate plane, we plot points, lines, etc. By joining various points on the coordinate plane, we can create shapes.
We use Formula and Theorems to solve the geometry problems.
A formula is a mathematical equation to solve a geometry problem while a theorem is a statement that is proved using previously known facts.
For example, the “Pythagoras Theorem” proved that a2 + b2 = c2 for a right-angled triangle, where a and b are the sides of the right-angled triangle, and c is the hypotenuse.
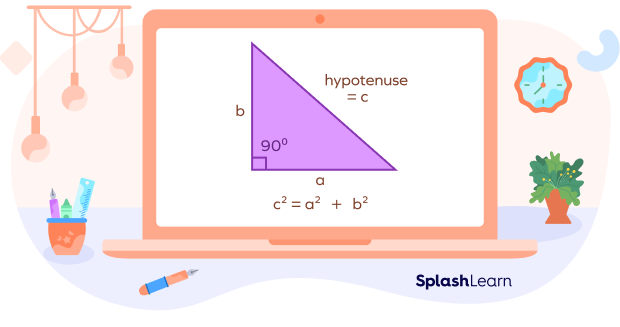
However, a2 + b2 = c2 is the formula for finding the hypotenuse of a right-angled triangle.
Fun Facts
– The word geometry is made from the Greek words “Geo” meaning “earth” and “metry” meaning “measurement”.
Solved Examples On Geometry
- Is the given shape an example of a simple closed curve that is also a polygon?
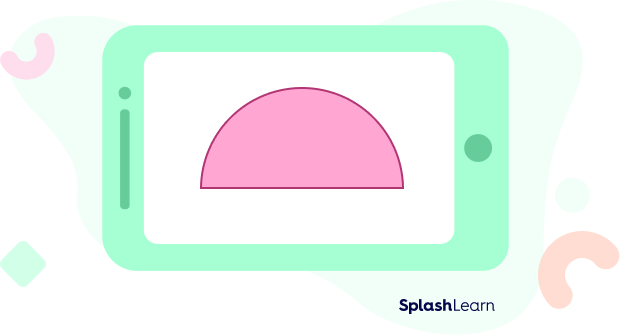
Solution:
A closed shape that does not cross itself is a simple closed curve. Polygons are closed shapes formed of only straight lines like triangles, rectangles, pentagons and so on.
The given figure is curved and is not made of only straight lines, this is not a polygon.
- In a triangle ABC, right angled at B, if ∠C=45° what is the measure of ∠A?
Solution: △ ABC is the given right triangle with ∠B=90°.
Sum of the angles of a triangle = 180°
∠A+∠B+∠C=180°
∠A+∠C=180°-90°=90°
But, ∠C=45° hence ∠A=90°-45°=45°
- Identify the flat surfaces in the given prism.
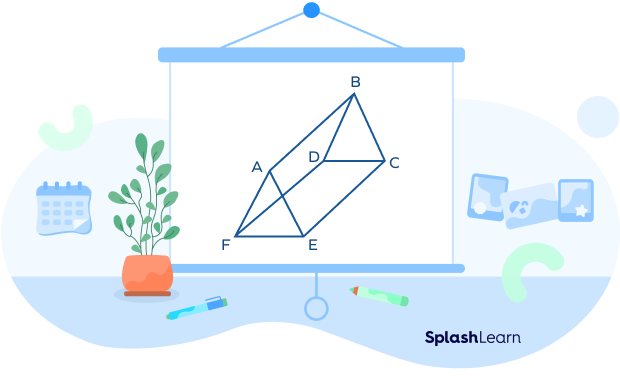
Solution:
The flat surfaces in the prism are as given below:
Rectangle AECB, Rectangle DCEF, Rectangle ABDF form the rectangular faces of the prism.
△ BCD and △ AEF form the triangular faces of the prism.
Practice Problems On Geometry
Geometry
Which of the following is a simple closed curve?
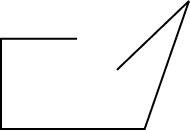
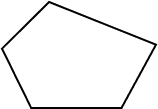
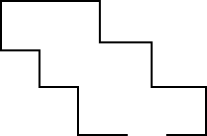
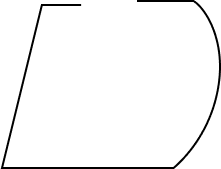
A closed shape that does not cross itself is a simple closed curve. It has the same start and end points.

Which of the following is a 3d shape?




The given shape is a 3d shape and is called a cube.

How many sides and corners does the given figure have?

The star shaped figure is made of 10 straight lines. Thus, it has 10 sides and 10 corners.
Frequently Asked Questions On Geometry
What is the relationship between mathematics and geometry?
Mathematics is an umbrella term for various disciplines that focus on logic and abstract concepts. Geometry is one of the branches of mathematics that deals with shapes and sizes of figures and their properties.
What are some applications of geometry?
Geometry can be applied to many areas such as architecture, electronics, engineering, and construction. It can also be used in fields like science to develop projects or programs for space exploration.
What is the main difference between 2D and 3D shapes?
The main difference between 2D and 3D shapes is the absence of depth or height in 2D shapes. They are flat figures. 3D shapes exist in three dimensions with length, breadth, and height and do not appear flat.
What is the difference between algebra and geometry?
Algebra is a branch of mathematics that uses variables, in the form of letters, to act as numbers or quantities in equations and formulas. Geometry is a branch of mathematics that studies the sizes, shapes, positions, angles, and dimensions of things.
















