Solid Shapes: Introduction
Solid shapes, also known as solids, consist of 3 dimensions—length, breadth, and height. They are also known as 3-D (3-Dimensional) shapes. The main difference between flat shapes and solid shapes is that the flat shapes or plane shapes only have two dimensions and solid shapes have 3 dimensions.
These solid shapes occupy some space and are found in our day-to-day life.
We can feel, touch, and use them.
Definition of Solid Geometry: The study of 3-dimensional objects, their volume, surface area, properties is called the ‘solid geometry’.
The geometrical figures are classified based on the dimensions as follows:
- Zero-dimensional shape – A zero-dimensional shape is the shape that has no length, no breadth and no height. For example: a point.
- One-dimensional shape – A one-dimensional shape has only one dimension. For example, a line has a length as its dimension.
- Two-dimensional shapes – A shape that has length and breadth as two dimensions. For example: square, triangle, rectangle, parallelogram, trapezoid, rhombus, quadrilateral, polygon, circle, etc.
- Three-dimensional shapes – A shape with three dimensions, i.e., length, breadth and height. For example: cube, cuboid, cone, cylinder, sphere, pyramid, prism, etc.
- Higher-dimensional shapes – There are a few shapes expressed in dimensions higher than 3, but we usually do not study them in middle-level mathematics.
Recommended Games
What are Solid Shapes in Geometry?
Look at these two shapes.
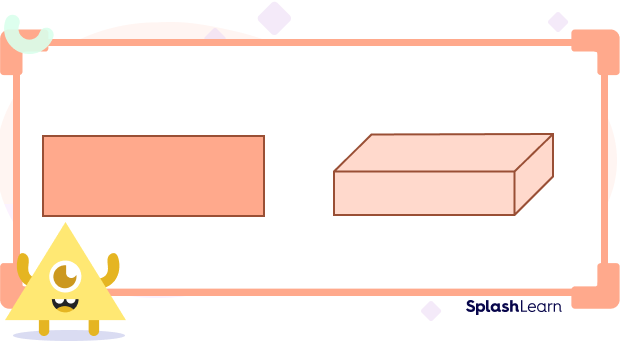
While the rectangle only has a length and breadth, the cuboid also has the dimension of height, making it a solid shape. The rectangle is a plane figure, whereas the cuboid looks more like a real solid figure.
Solid shapes are three-dimensional (3D) geometric shapes that occupy some space and have length, breadth, and height. Solid shapes are classified into various categories. Some of the shapes have curved surfaces; some of them are in the shape of pyramids or prisms.
The following image shows a cuboid or a rectangular prism with its 3 dimensions. The lower surface on which a solid object stands is called its base. The given cuboid has a rectangular base.
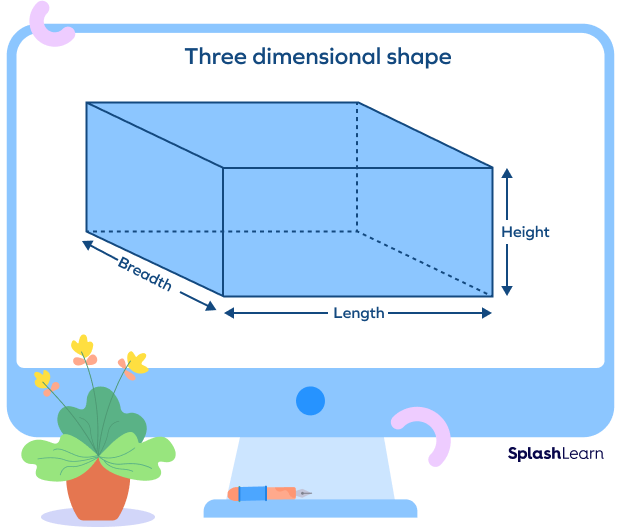
You will find multiple objects that fit the solid shape criteria if you look around. Living in a three-dimensional world, we will likely come across solid shapes more often than two-dimensional shapes. There are endless examples of solid shapes surrounding us, from a matchbox to a birthday cap.
There are four features of solid shapes that make them different from plane shapes, which are discussed below.
Recommended Worksheets
Elements of Solid Shapes
Solid shapes and objects are different from two-dimensional (2D) shapes and objects because of the presence of the 3 dimensions—length, breadth, and height.
As a result of these 3 dimensions, these objects have faces, edges, and vertices.
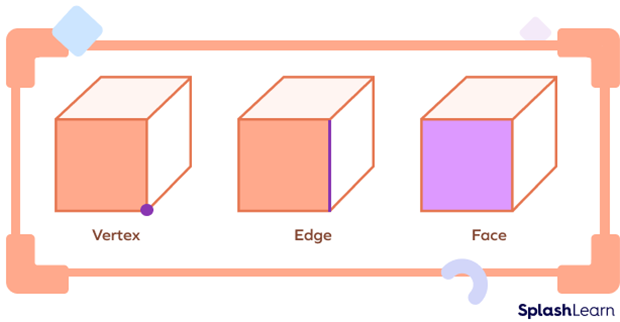
- Faces: A face is a single flat surface of a solid shape, and there can be more than one face of a shape.
- Vertices: A vertex is a point where two or more lines meet, forming a corner. It is also the point of intersection of edges.
- Edges: An edge is a line segment at the boundary of a solid shape that joins one vertex to another. The edges serve as the junction of two faces.
- Volume: Every solid shape occupies some volume, which is not the case in a two-dimensional object.
Solid Shapes and Their Properties
Solid shapes are three-dimensional objects. Look at your surroundings! Every other three-dimensional object, be it a cup, ball, an ice cream cone, or TV, is an example of a solid shape. These objects occupy some space and have length, width as well as height.
Three-dimensional shapes have properties that set them apart from two-dimensional shapes: faces, vertices, edges, and volume. The properties allow you to determine whether the shape is two-dimensional or three-dimensional and also which three-dimensional shape it is.
Let’s explore some solid shapes and related solid figure formulas. Some common solid shapes names are:
- Cube
- Cuboid
- Cylinder
- Cone
- Sphere
- Pyramid
- Prism
Types of Solid Shapes
Sphere

A sphere is round in shape, like the moon or a ball. It is perfectly symmetrical, and it has no edges or vertices. So, it has only one surface. Every point on a sphere is located such that it is at an equal distance from a central point on the sphere.
The following are formulas related to the sphere shape:
Total Surface Area $= 4\pi r^{2}$, where r is the radius of the sphere.
Volume $= \frac{4}{3} \pi r^{3}$, where r is the radius of the sphere.
A sphere is a solid figure with a round shape. It has a curved surface, defined in three-dimensional space. Every point on the surface of a cube is equidistant from the center.
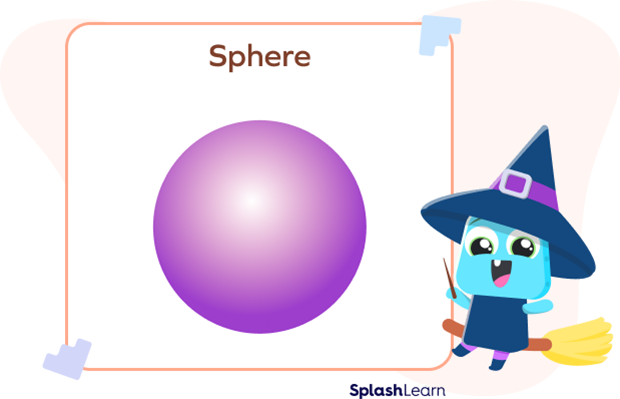
Properties of a Sphere
1. A sphere has no edges or vertices (corners).
2. It has one surface, i.e., curved.
3. It is shaped like a ball and is perfectly symmetrical.
4. All points on the surface of the cube are the same distance $(r)$ from the center.
Surface Area of a Sphere
Let the radius of the sphere be r units.
Curved Surface Area/Total Surface Area/Surface Area $= 4\pi r^{2}$ square units.
Volume of a Sphere
Volume of a cube $= \frac{4}{3} \pi r^{3}$ cubic units
Cylinder
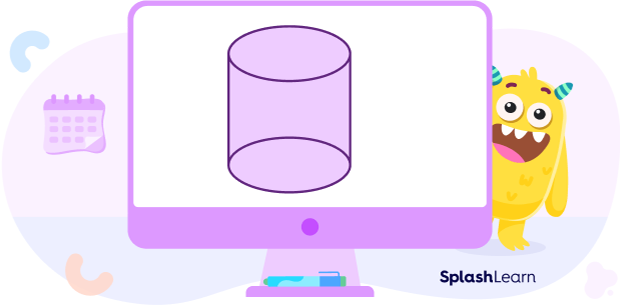
Consider a can of your favorite fruit juice. It has a flat base and top, both the same size. Going from the base to the top, the shape of the cylinder remains the same. Also, it has one curved side that connects the base to the top. A cylinder is a solid shape with a curved surface joining its top and bottom circular bases. Think of it as a can of toffees.
The following are formulas related to the cylinder shape:
Curved Surface Area $= 2\pi rh$, where r is the radius of the base and h is the height.
Total Surface Area $= 2\pi r(h + r)$, where r is the radius of the base and h is the height.
Volume $= \pi r^{2}$ $h$, where r is the radius of the base and h is the height.
A cylinder is a solid shape that holds two parallel bases that are circular in shape and are joined by a curved surface (like a tube), at a fixed distance.
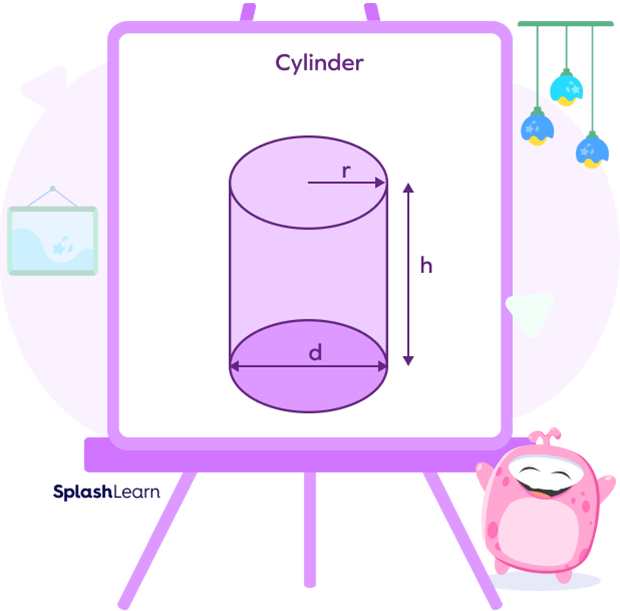
Properties of a Cylinder
1. A cylinder has two flat surfaces, i.e., base and top.
2. It has one curved surface.
3. The bases of the cylinder are always congruent and parallel.
4. It has two identical ends that are either circular or oval in shape.
Surface Area of a Cylinder
Let the radius and height of the cylinder be r and h units respectively.
Curved Surface Area $= 2\pi r h$ square units
Total Surface Area/Surface Area $= 2\pi r (h + r)$ square units.
Volume of a Cylinder
Volume of a cube $= \pi r^{2} h$ cubic units
Cuboid
Any box-shaped object resembles the shape of a cuboid. It has a total of six faces, and all the angles of the cuboid stand at a right angle. An example of a cuboid shape is a matchbox or a smartphone. It is a solid rectangular shape with six faces, each of which is a rectangle. It has a total of eight vertices and twelve edges. Often, it is also referred to as a rectangular prism.
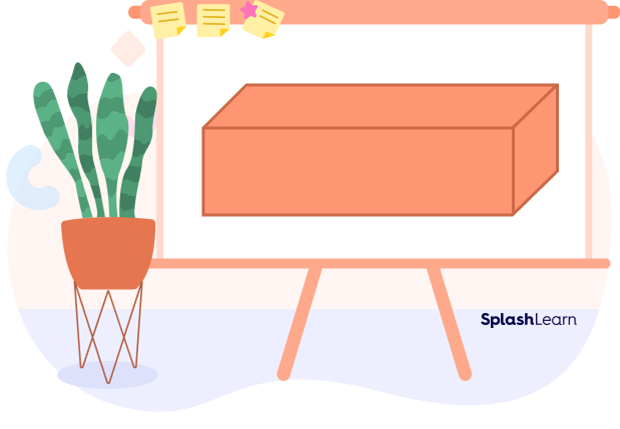
A cuboid is a solid that has 6 rectangular faces, 8 vertices, and 12 edges.
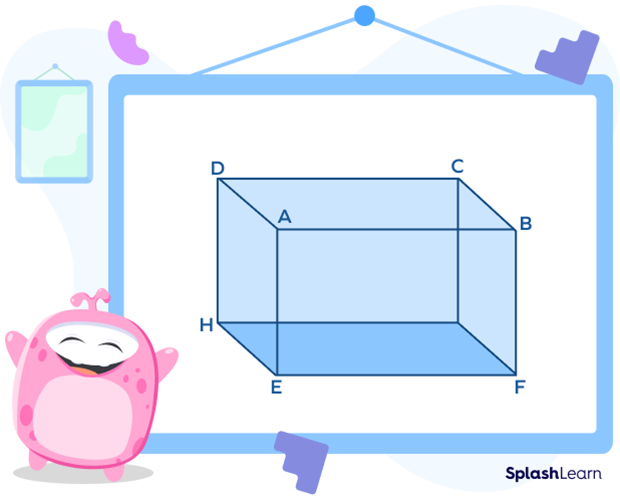
Properties of a Cuboid
1. It has all the faces in the shape of a rectangle.
2. All the faces or sides of a cube have different dimensions.
3. The angles of planes of the cube are the right angle.
4. Each of the faces of a cube meet the other four faces.
5. Each of the vertices of a cube meet the three faces and three edges.
6. The edges that are opposite to each other are parallel.
Surface Area of a Cuboid
Let the length, breadth and height of a cuboid be $l$,$b$, and $h$ respectively.
Curved Surface Area $= 2h(l + b)$ square units.
Total Surface Area/Surface Area $= 2(lb + bh + h)$ square units.
Volume of a cuboid
Volume of a cube $= l \times b \times h$ cubic units
The following are formulas related to the cuboid shape:
Curved Surface Area $= 2h (l + b)$, where $l = \text{length}, b = \text{width}, h = \text{height}$ of the cuboid.
Total Surface Area $= 2 (lb + bh + hl)$ ,where $l = \text{length}, b = \text{width}, h = \text{height}$ of the cuboid.
Volume $= lbh$, where $l = \text{length}, b = \text{width}, h = \text{height}$ of the cuboid.
Cube

Consider a cube of ice in the tray of your fridge. All six faces of the cube are the same, which also makes it a square prism. Even a Rubik’s Cube or a playing dice are examples of a cube. This is what makes it a solid 3D object. A cube is a symmetrical three-dimensional shape contained within six equal squares. It may be solid or hollow.
A cube is a solid that has 6 square faces, 8 vertices, and 12 edges.
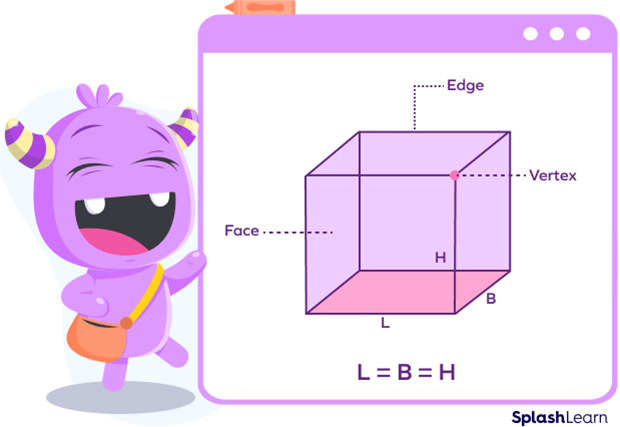
Properties of a Cube
1. It has all the faces in the shape of a square.
2. All the faces or sides of a cube have equal dimensions.
3. The angles of planes of the cube are the right angle.
4. Each of the faces of a cube meet the other four faces.
5. Each of the vertices of a cube meet the three faces and three edges.
6. The edges that are opposite to each other are parallel.
Surface Area of a Cube
Let the edge of a cube be $a$ units.
Curved Surface Area $= 4a^{2}$ square units.
Total Surface Area/Surface Area $= 6a^{2}$ square units.
Volume of a cube
Volume of a cube $= a^{3}$ cubic units
The following are formulas related to the cube shape:
Curved Surface Area $= 4a^{2}$, where $\text{a} =$ edge length of the cube.
Total Surface Area $= 6a^{2}$, where $\text{a} =$ edge length of the cube.
Volume $= a^{3}$, where $\text{a} =$ edge length of the cube.
Cone

A cone is a distinctive three-dimensional geometric figure with a flat and curved surface pointed toward the top. A cone has 3 dimensions—its radius, height, and slant height.
A birthday cap and a funnel are some examples of the cone shape.
The following are formulas related to the cone shape:
Curved Surface Area $= \pi rl$, where r is the radius of the base and l is the slant height.
Total Surface Area $= \pi r (l + r)$, where r is the radius of the base and l is the slant height.
Volume $= \frac{1}{3}\pi r^{2} h$, where r is the radius of the base and h is the height.
A cone is a solid shape that has a flat surface and a curved surface, pointing towards the top. It is formed by a set of line segments connected from the circular base to a common point, which is known as the apex or vertex.
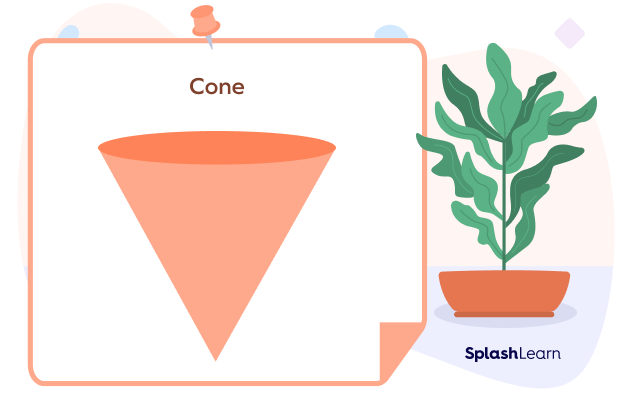
Properties of a Cone
1. It has a circular or oval base with an apex or a vertex.
2. It has one curved surface and one flat surface.
3. A cone is a rotated triangle.
Surface Area of a Cone
Let the radius and slant height of the cone be $r$ and $l$ units respectively.
Curved Surface Area $= \pi r l$ square units
Total Surface Area/Surface Area $= \pi r(l + r)$ square units.
Volume of a Cone
Volume of a cube $= \frac{1}{3}\pi r^{2} h$ cubic units
Pyramid

The mention of a pyramid brings to mind images of the great structures built in Egypt. The pyramid’s base is flat with straight edges, and the remaining faces of the pyramid are triangles. There are no curves in a pyramid.
It is a polyhedron with a polygon base and all lateral faces in a triangle shape. Depending on the alignment with the center of the base, a pyramid can be further classified as a regular or an oblique pyramid.
A pyramid is a polyhedron with a polygon base and all its lateral faces are triangular in shape. Pyramids are typically categorized by the shape of their bases.
A pyramid with:
- A triangular base is known as a tetrahedron.
- A quadrilateral base is known as a square pyramid.
- A pentagon base is known as a pentagonal pyramid.
- A regular hexagon base is known as a hexagonal pyramid.
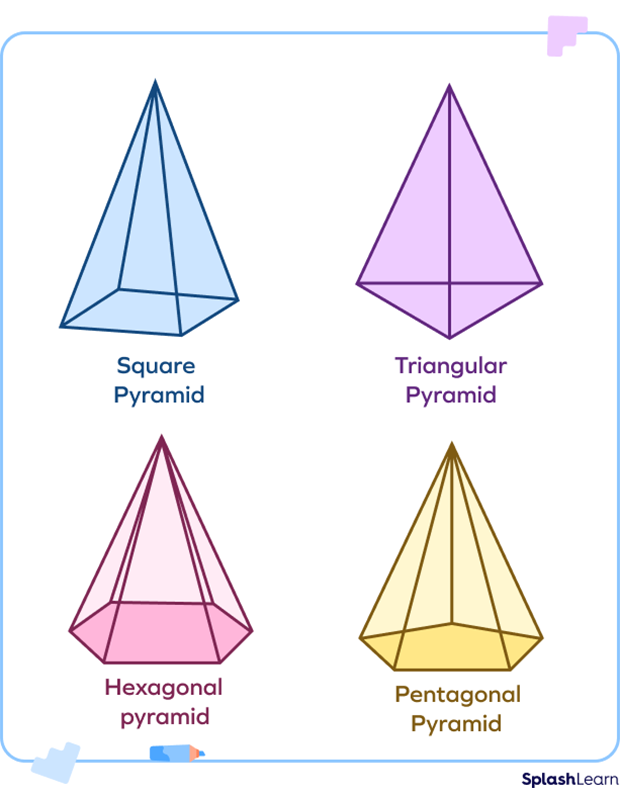
$\text{BA} =$ base area, $\text{P} =$ perimeter, $\text{A} =$ altitude, and $\text{SH} =$ slant height
Properties of a Pyramid
1. A pyramid is a polyhedron with a polygon base and a vertex with straight lines.
2. It has one curved surface and one flat surface.
3. A cone is a rotated triangle.
Surface Area of a Pyramid
$\text{BA} =$ base area, $\text{P} =$ perimeter, $\text{A} =$ altitude, and $\text{SH} =$ slant height
Surface Area $= BA + \frac{1}{2} \times P \times SH$ square units.
Volume of a Cone
Volume of a cube $= \frac{1}{3} BA^{2}$ cubic units
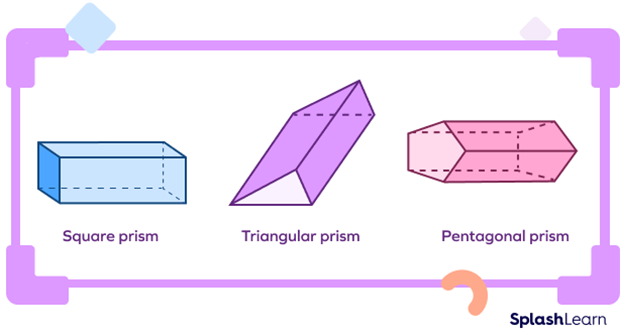
Prism

A prism is a solid object with identical ends, flat faces, and no curves.
A prism has two identical shapes facing each other and can be of different types, such as triangular prisms, hexagonal prisms, pentagonal prisms, etc. A unique feature of a prism is that it has the same cross-section throughout its length.
A prism is a solid shape with two identical shapes that faces each other. The different types of prisms are triangular prisms, square prisms, pentagonal prisms, hexagonal prisms, etc. Prisms are also broadly classified into regular prisms and oblique prisms.
Properties of a Prism
1. A prism has identical polygonal ends and flat faces.
2. It has the same cross-section along its length.
Surface Area of a Prism
$\text{BA} =$ base area, $\text{P} =$ perimeter, $\text{A} =$ altitude, and $\text{SH} =$ slant height
Surface Area $= 2 \times BA \times P \times H$ square units.
Volume of a Prism
Volume of a cube $= BA \times H$ cubic units
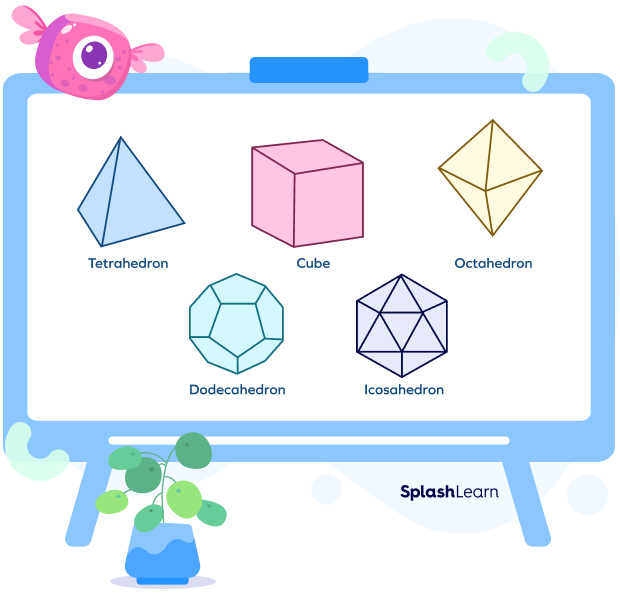
Polyhedrons/Platonic Solids
Platonic solids have identical faces to regular polygons. There are five polyhedrons.
- A tetrahedron is a platonic solid with four equilateral-triangular faces.
- A pentahedron is a solid figure with 5 faces.
- An octahedron is a platonic solid with eight equilateral-triangular faces.
- A dodecahedron is a platonic solid with twelve pentagon faces.
- An icosahedron is a platonic solid with twenty equilateral-triangular faces.
- A hexahedron or cube is a platonic solid with six square faces.
Conclusion
In this article, we learned about the solid figures. A solid figure has three dimensions, namely length, breadth and height. To read more such informative articles on other concepts, do visit our website. We, at SplashLearn, are on a mission to make learning fun and interactive for all students.
Solved Examples
Example 1: If we want to build a solid sphere by filling it with cement, how much cement will be required to construct one sphere of radius 10 cm?
Solution: We know that the volume of a sphere is given by
Volume $= \frac{4}{3}\pi r^{3}$, where r is the radius of the sphere.
Here $r = 10$ cm,
Therefore, Volume of given sphere $= \frac{4}{3} \times 3.14 \times 10 \times 10 \times 10 = 4186.6$ cubic centimeters
Example 2: Calculate the volume of a cylinder with a radius of 3 cm and a height of 9 cm.
Solution: Using the formula to calculate the volume of a cylinder, we get
Volume $=\pi r^{2} h$, where r is the radius of the base and h is the height.
Here $r = 3$ cm and $h = 9$ cm
Therefore, volume of the given cylinder is,
$\text{V} = 3.14 \times 3 \times 3 \times 9 = 254.34$ $cm^{3}$.
Example 3: What will be the surface area of a cuboid whose dimensions are as follows:
Length $= 8$ cm
Breadth $= 5$ cm
Height $= 7$ cm
Solution: To calculate the total surface area of a cuboid, we can use the formula
Total surface area $= 2 \times (lb + bh + lh)$, where $l = \text{length}, b = \text{width}, h = \text{height}$ of the cuboid.
Here $l = 8$ cm, $b = 5$ cm, $h = 7$ cm
Therefore, total surface area of the given cuboid is
Total Surface Area $= 2 \times ( 8 \times 5 + 5 \times 7 + 8 \times 7)$
$= 2 \times (40 + 35 + 56)$
$= 2 \times 131$
$= 262$ square centimeters.
Example 4. Find the curved surface area of a cylinder of radius 14 cm and height 10 cm.
Solution: Radius $(r) = 14$ cm
Height $(h) = 10$ cm
Curved surface area of cylinder $= 2\pi r h$
$= 2 \times \frac{22}{7} \times 14 \times 10 = 880$ $cm^{2}$
Example 5. Find the volume of a cube whose side is 10 cm.
Solution: Side of a cube $= a = 10$ cm
Volume of a cube $= 10 \times 10 \times 10 = 1000$ $cm^{3}$.
Example 6. Find the radius of the sphere whose surface area is 176 $cm^{2}$.
Solution: Surface area of sphere $= 4\pi r^{2}$
$176 = 4 \times \frac{22}{7} \times r^{2}$
$r^{2} = \frac{176 \times 7}{22 \times 4} = 14$ cm
Example 7. Find the lateral surface area of a regular pyramid with a triangular base if each edge of the base measures 10 cm and the slant height is 4 cm.
Solution: Perimeter $= 3 \times 10 = 30$ cm
Lateral surface area $= \frac{1}{2} \times P \times SH = \frac{1}{2} \times 30 \times 4 = 60$ $cm^{2}$.
Example 8. Find the capacity of ice cream $(in$ $l)$ contained in a cone with height 24 cm and diameter is 14 cm.
Solution: Height $(h) = 24$ cm
Diameter $(d) = 14$ cm
Radius $(r) = 7$ cm
Volume $= \frac{1}{3}\pi r^{2} h$
$= \frac{1}{3} \times \frac{22}{7} \times7 \times 7 \times 24 = 1232$ $cm^{3}$
$1$ $cm^{3} = 0.001$ $l$
$1232$ $cm^{3} = 1.232$ $l$
Practice Problems
Solid Shapes - Definition, Types, Properties, Examples
What will be the volume of a sphere with a radius of 7 cm?
Volume $= \frac{4}{3}\pi r^{3}$, where r is the radius of the sphere.
Here $r = 7$ cm,
Therefore, Volume of given sphere $= \frac{4}{3} \times 3.14 \times 7 \times 7 \times 7 = 1436.02$ cubic centimeters
Find the volume of a cube that has an edge of length 5 cm.
We know that volume of a cube is given by
Volume $= a^{3}$, where a = edge length of the cube.
For the given cube, $a = 5$ cm
Therefore, Volume of given cube $= 5 \times 5 \times 5 = 125$ $cm^{3}$
Which of the following is not a solid shape?
A circle is a two-dimensional object since it is a closed and flat figure. We can call it a plane figure with no sides or edges.
Calculate the volume of a right cylinder that has a radius of 5 cm and a height of 10 cm.
Using the formula to calculate the volume of a cylinder, we get
Volume $=\pi r^{2} h$, where r is the radius of the base and h is the height.
Here $r = 5$ cm and $h = 10$ cm
Therefore, volume of the given cylinder is,
$\text{V} = 3.14 \times 5 \times 5 \times 10 = 785$ $cm^{3}$
Which of the following is not a solid shape?
A triangle is a two-dimensional shape that has only 2 dimensions whereas a solid shape has 3 dimensions.
Find the curved surface area of a cuboid whose length is 10 cm, breadth is 6 cm and height is 4 cm.
Length $(l) = 10$ cm, Breadth $(b) = 6$ cm and Height $(h) = 4$ cm
Curved Surface Area $= 2h (l + b)$
$= 2 \times 4 \times (10 + 6) = 8 \times 16 = 108$ $cm^{2}$
Which of the following solid shapes does not have a flat surface?
A sphere is a three-dimensional solid that has only a curved surface.
The number of faces of a hexahedron is ____.
A hexahedron or a cube has 6 faces.
Which of the following is not a regular polyhedron?
A regular polyhedron is made of regular polygons. A cuboid is made of rectangles that are not regular polygons.
Frequently Asked Questions
What are platonic solids?
Platonic solid shapes have identical faces and are also known as polyhedrons, which can be of five types, namely, tetrahedron, octahedron, dodecahedron, icosahedron, and hexahedron.
How many edges does a cylinder have?
A cylinder does not have any edges, but it has two faces.
Does every solid shape have at least one face, edge, and vertex?
Solid shapes don’t need all faces, edges, and vertices. For example, a sphere has one rolling surface but no edges or vertices.
What is the difference between solid shapes and flat shapes?
Solid shapes are the shapes which have three dimensions namely length, breadth and height. For example: cylinder, cone, etc. Flat shapes are the shapes that have 2 dimensions namely length and breadth. For example: triangle, oval, etc.
What is the difference between a pyramid and a prism?
A prism is a polyhedron whose two polygonal bases and other faces are rectangular. For example: Square prism, pentagonal prism, etc. A pyramid is a polyhedron that has one polygon base and other faces are triangular. For example: square pyramid, triangular pyramid, etc.
What is the surface area of a cube if we remove the top of the cube?
If the top of the cube is removed, only 5 surfaces will be left. Each surface has $a^{2}$. So, the surface area $= 5a^{2}$
What is the Euler’s Formula for solid shapes?
Euler’s Formula is: $\text{F} + \text{V} = \text{E} + 2$ where F, V, and E are the number of faces, number of vertices and number of edges respectively.
What is the perimeter of a cube?
There are 12 edges in a cube and all the edges are equal. So, the perimeter of a cube $= 12a$ if $a$ is the edge of the cube.
What are solids in math?
Solids in math are 3-dimensional objects that occupy space. They are also called 3D shapes, solid shapes or solid figures.




















