Have you ever noticed a candle or your favorite can of chips? They have a specific structure where they stand properly upright if you lay them down by their base, but you can roll them anywhere if you lay them down on their side.

Such objects follow the structure of the three-dimensional shape called a cylinder. A cylinder is made up of a rolled surface with a circular top and a circular base.
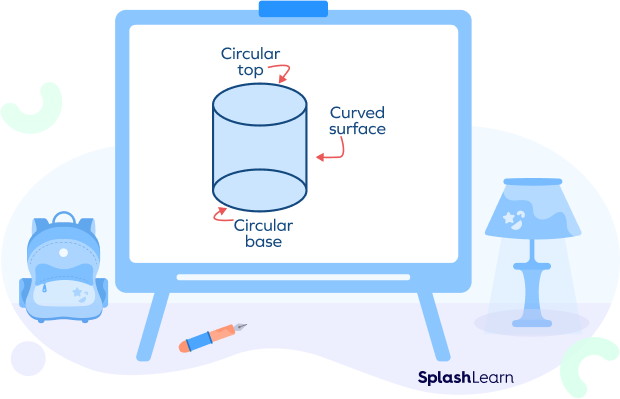
You can construct your own cylinder by folding a rectangle along its length and closing the rolled structure, thus formed with two identical circles at its top and bottom.
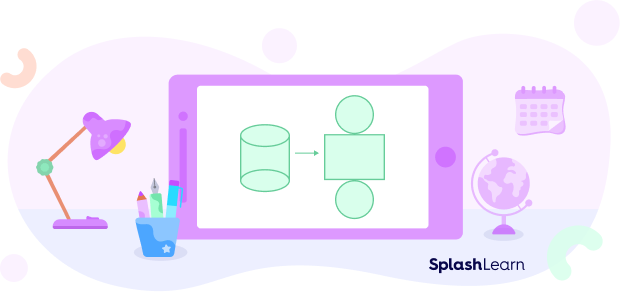
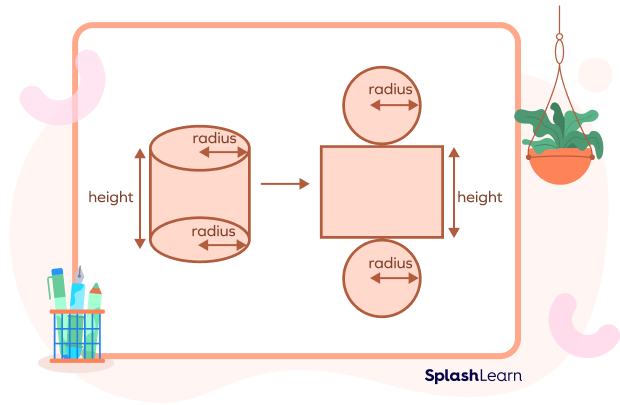
As evidenced by the net of the cylinder, the height of the cylinder depends upon the length of the rectangle, and the radius of a cylinder depends on the two circles at its top and bottom.
Properties of a Cylinder
There are so many properties that make a cylinder unique. Some of them are:
- A cylinder has no vertex.
- The curved surface of a cylinder is actually just a folded rectangle.
- The top and base of a cylinder can actually be varied to produce different types of cylinders.
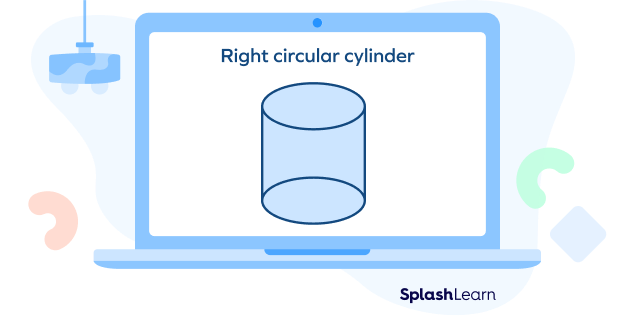
If the axis of the cylinder is a straight vertical line, or the cylinder stands totally upright with two identical circular bases, it is called a right circular cylinder.
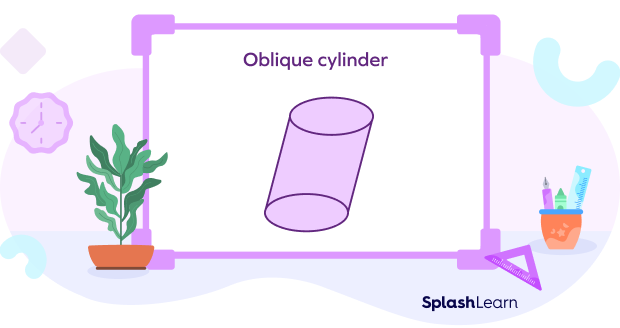
If it looks like the cylinder is leaning to either right or left, trying to eavesdrop on someone, and has identical circular bases, it is called an oblique cylinder.
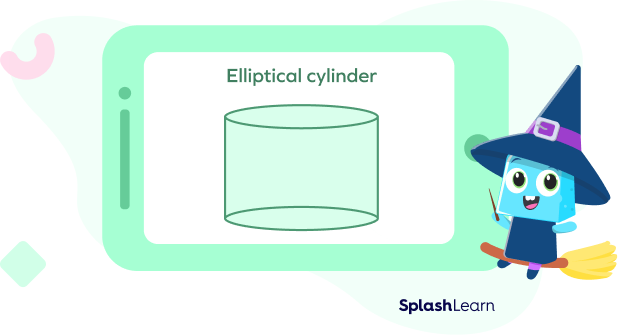
If you think the cylinder is trying to get through an alleyway or trying to hold its breath to look slimmer, it is actually just an elliptical cylinder whose bases are not circles but ellipses or ovals.
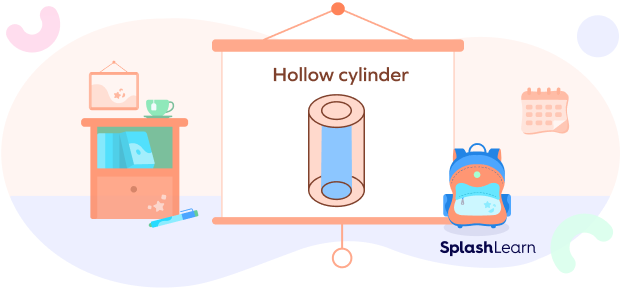
Another type of cylinder that you can find a lot of examples of in your surrounding is called the hollow cylinder. “Hollow”, because it is empty from the inside; for example, a cold drink straw or a well.
Recommended Games
Area of a Cylinder
There are two types of areas associated with a cylinder:
Curved Surface Area
The curved surface area of a cylinder can simply be defined as the area of the rolling part of the cylinder, i.e., the area of the curved part.
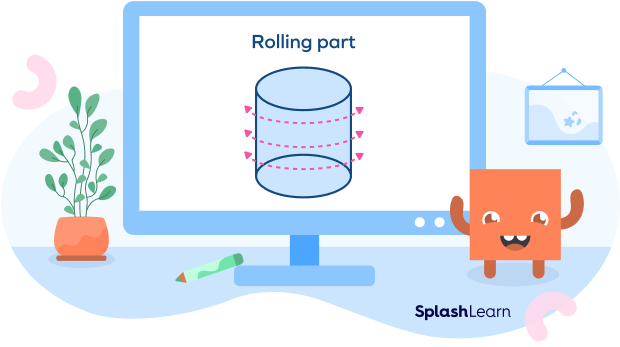
The formula for the curved surface area of the cylinder is given as
2 ✕ $\pi$ ✕ r ✕ h
Where r stands for the radius of the base and h stands for the height of the cylinder.
Total Surface Area
The total surface area of a cylinder is the sum of its curved surface area and the sum of the areas of its two bases:
Total surface area = Curved surface area + 2 ✕ area of circular base
=2 $\pi$ r h + 2 ✕ $\pi$ r2
=2 $\pi$ r( h + r)
Volume of a Cylinder
The volume of a cylinder is defined as the amount of space it has that can be filled. Suppose you had a cylinder that is absolutely empty from inside. If we start filling it with water, then the amount of water that the cylinder can hold will be referred to as its volume.
The volume of a cylinder is given by the formula: $\pi$ ✕ r2 ✕ h.
Recommended Worksheets
Solved Examples
Question 1: Find the volume of the given figure in the nearest cubic centimeter.
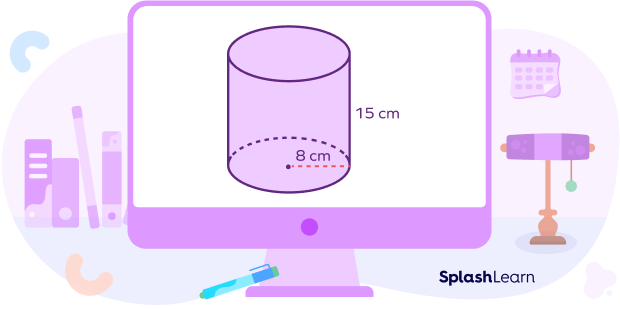
Answer: The formula of the cylinder is πr²h, here r = 8 cm and h = 15 cm
Therefore, volume of given cylinder = π ✕ 8 ✕ 8 ✕ 15 = 3016 cubic centimeters
Question 2: Find the curved surface area of a cylinder of radius 5 cm and height 7 cm.
Answer: The formula for the curved surface area of the cylinder is given as 2 ✕ π ✕ r ✕ h.
For the given cylinder we have r = 5 cm and h = 7 cm.
Therefore, curved surface area of given cylinder = 2 ✕ π ✕ 5 ✕ 7 = 220 square centimeters.
Practice Problems
Cylinder
What is the formula for the curved surface area of a cylinder?
The curved surface area of a cylinder is the circumference of the base times the height of the cylinder.
Which of the following objects are cylindrical?
A tissue roll is like a hollow cylinder.
Find the volume of the cylinder with a radius of 14 cm and a height of 10 cm.
Volume of cylinder = πr²h,
Here, r = 14 cm and h = 10 cm
Therefore, Volume of cylinder = π ✕ 14 ✕ 14 ✕ 10 = 6160 cubic centimeters.
What is the total surface area of a cylinder whose radius of the base is 2 cm and height is 5 cm?
The total surface area of a cylinder is given by 2πr (h + r).
Here, r = 2 cm and h = 5 cm.
Therefore area of given cylinder = 2 ✕ π ✕ 2 ✕ (5 + 2)
= 2 ✕ π ✕ 2 ✕ 7
= 88 square centimeters
Frequently Asked Questions
What are some real-life examples of cylinders?
Ans: Some real life examples of cylinders include soda bottles, straws, pencils, and remote batteries.
How many faces does a cylinder have?
Ans: A cylinder has 3 faces: two circular faces and a curved surface.
How many edges does a cylinder have?
Ans: An edge can be defined as a straight line where any two faces of a geometrical shape meet. Although a cylinder has 3 faces, its surface is curved in nature and not a straight line. Hence a cylinder does not have any edges.
How many vertices does a cylinder have?
Ans: The vertex of any shape is defined as the corner point where its sides or edges meet. Since a cylinder has no edges, it does not have any vertices.


















