Area in Math – Definition, Composite Figures, FAQs, Examples

Definition of Area

Area is defined as the total space taken up by a flat (2-D) surface or shape of an object.

The space enclosed by the boundary of a plane figure is called its area. The area of a figure is the number of unit squares that cover the surface of a closed figure. Area is measured in square units like cm² and m². Area of a shape is a two dimensional quantity. 

The term “area” refers to the space inside the boundary or perimeter of a closed shape. The geometry of such a shape contains at least three sides joined together to form a boundary. Symbolic representation of such space in mathematics refers to the “area” formula. To represent and draw real-life objects, designers and architects use different shapes such as circle, triangle, quadrilateral, and polygon. 

The invention of the wheel was the prime step of translating objects into geometric shapes. In the early days, the interpretation of “area” using a formula for geometric shapes evolved from the experiments conducted by Archimedes.

What is the formula of Calculating Area?

We can calculate the area of a shape using a grid. The area of any shape is the number of square units that can fit into it. The grid is made of many squares and each square has sides 1 unit by 1 unit, i.e., the area of each square is 1 square unit. Each square is known as a unit square. 

Take a pencil and draw a square on a piece of paper. It is a 2-D figure. The space the shape takes up on the paper is called its Area. 

Now, imagine your square is made up of smaller unit squares. The area of a figure is counted as the number of unit squares required to cover the overall surface area of that particular 2-D shape. Square cms, square feet, square inches, square meters, etc., are some of the common units of area measurement.

The easiest method to interpret the area of geometric shapes is using “unit squares”. A unit square is a square with each of its side length measuring 1 unit. Using this as a basis, the area of a polygon is the number of unit squares within a shape. 

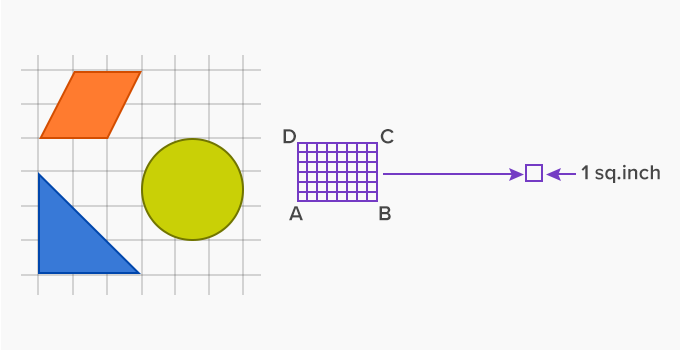
To find out the area of the square figures drawn below, draw unit squares of 1-centimeter sides. Thus, the shape will be measured in $cm^{2}$, also known as square centimeters.

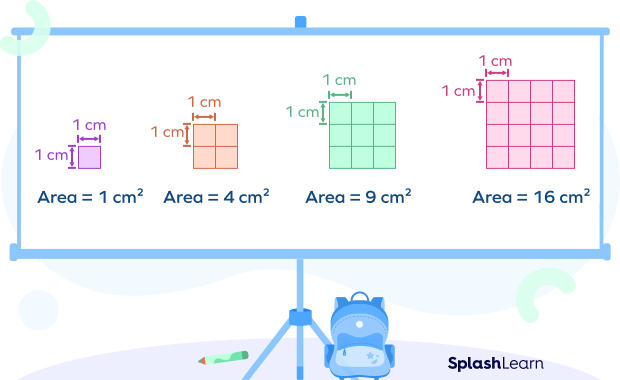
Here, the area of the shapes below will be measured in square meters $(m^{2})$ and square inches $(in^{2})$.

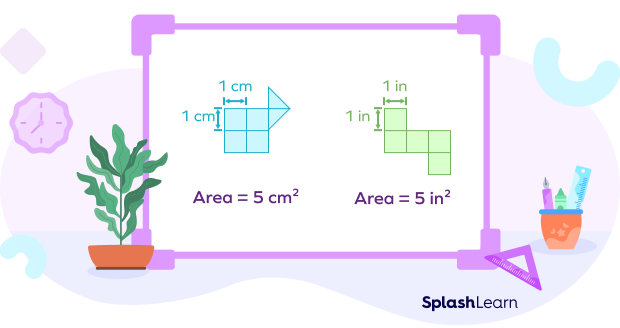
The area of a shape is the number of shaded unit squares. In the figure below, the number of shaded unit squares $= 24$. Hence, the area of the shape $= 24$ square units.

How to calculate the area if there are also half unit squares in the grid? 

To understand that, let us take one more example: 

Step 1: Count the full squares.

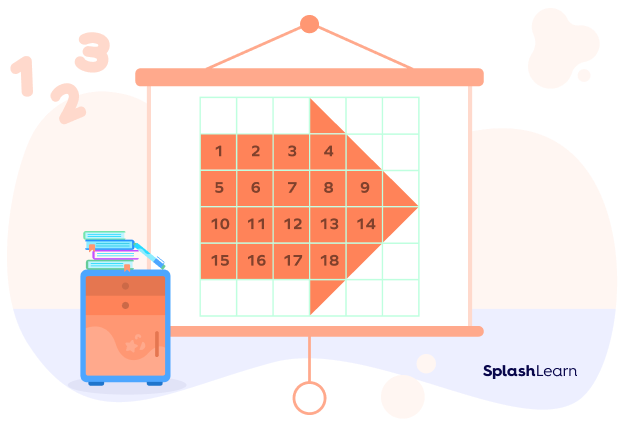
There are 18 full squares. 

Step 2: Count the half squares. 

On counting, we see that there are 6 half squares.

Step 3: 1 full square $= 1$ square unit

So, 18 full square $= 18$ square units

1 half square $= \frac{1}{2}$ square unit

6 half squares $= 3$ square units

Total area $= 18 + 3 = 21$ square units. 

Origin of the Term: Area

The term ‘area’ originated from Latin, meaning ‘a plain piece of empty land’. It also means ‘a particular amount of space contained within a set of boundaries’.

More about Area

Look at the carpet in your home. To buy a carpet that fits the floor, we need to know its area. Or the carpet will be bigger or smaller than the space! Some other instances when we need to know the area are while fitting tiles on the floor, painting the wall or sticking wallpaper to it, or finding out the total number of tiles needed to build a swimming pool.

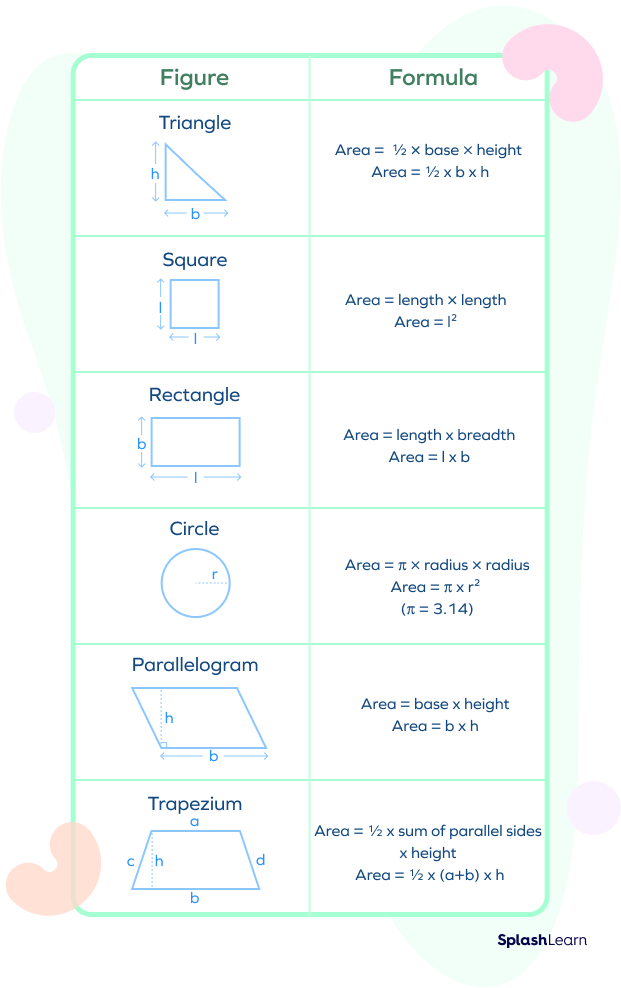
Formulas for Calculating Area

We are surrounded by so many 2-D shapes: circle, triangle, square, rectangle, parallelogram, and trapezium. You can draw all of these shapes on your paper. Every shape is different and unique, so its area is also calculated differently. To find the area, first, identify the shape. Then, use the appropriate formula from the list given below to find its area. 

• The area of an object can be explained as the amount of material required (such as paper, fabric, tiles) to cover the surface in a 2-dimensional plane.
• For 3-dimensional planes, such as cuboid, cube, sphere, etc., it is referred to as surface area. 

Areas of Composite Figures 

Every plane figure cannot be classified as a simple rectangle, square, triangle, or typical shape in real life. Some figures are made up of more than one simple 2-D shape. Let us join a rectangle and a semicircle. 

These shapes formed by the combination of two or more simple shapes are called “composite figures” or “composite shapes”.

For finding the area of a composite figure, we must find the sum of the area of all the shapes in it. So, the area of the shape we just drew will be the area of the rectangle, l b plus half the area of the circle, ½ x πr², where l and b are the length and breadth of the rectangle and r is the radius of the semicircle.

If we draw a semicircle below a triangle, we get the composite shape:

The area of such a composite figure will be calculated by adding the area of the triangle and the area of the semicircle. 

Area of the a composite figure $= (\frac{1}{2} \times b \times h) \times (\frac{1}{2} + \pi r^{2})$

where r is the radius of the semicircle and b and h are the base and height of the triangle respectively. 

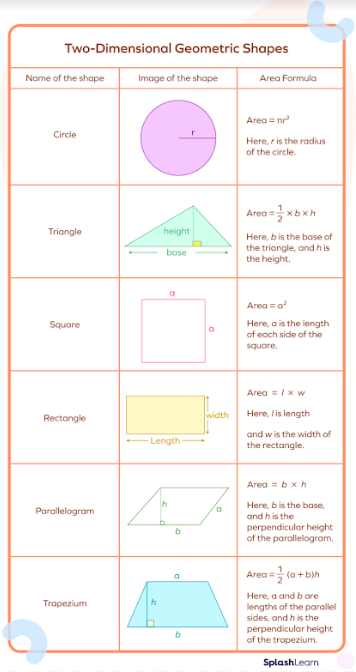
Area of 2-D Shapes

The table below lists the shapes and their formula to calculate area:

The table below summarizes some common 2D shapes and the area formula:

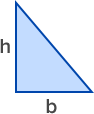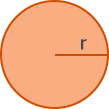Area $=  12 \times \text{base} \times \text{heightArea} =  12 \times b \times h$	$\text{Area} = \text{length} \times \text{length} \text{Area} = l^{2}$	$\text{Area} = \text{length} \times \text{breadthArea} = l \times b$	$\text{Area} = \pi \times \text{radius} \times \text{radiusArea} =  \pi \times r^{2} (\pi = 3.14)$

Area v. Perimeter

Area	Perimeter
The space occupied by a closed plane in a two dimensional shape is called area.	Perimeter is the measure of the length of the outer boundary of a closed shape.
Area is measured in squared units.	Perimeter is measured in units.
Example: Area of tiling the floor	Example: Perimeter of fencing the garden

Area v. Volume

Area	Volume
Area is defined for 2-dimensional space.	Volume is defined for 3-dimensional space.
The space occupied by a closed plane in a 2-dimensional shape is called area.	The space occupied by a 3-dimensional figure is known as volume.
Example: Area of tiling the floor	Example: Volume of the room

Real-life Applications

Here are a few ways in which you can apply the knowledge of the area of figures in your daily life.

• We can find the area of a gifting paper to check whether it will be able to cover a box or not.
• We can find the area of a square or circle to find the area of the signal board.
• The concept of area has been the foundation of geometry since the early days. Scientists and astronomers took the help of patterns and geometric shapes to understand and establish advanced concepts in science and mathematics. 
• In a modern aspect, the mathematical modeling of objects such as machines, tools, wheels as well as garment designing uses the concept of area and perimeter. It also serves as a basis for integral calculus to understand complex objects such as spheres and ellipses.

Fun Facts

1. The area of the disk was evaluated in the 5th century BCE by Hippocrates of Chios

2. Area of triangle is also calculated using Heron’s formula

Conclusion

So far, we have learned that area is the two-dimensional space any object takes. Learning about shapes and their area and perimeter becomes much more interesting when we understand them with real-life applications. The use of area in practical life is while buying a new house, land, or even a small painting. 

Solved Examples On Area

1. A circle has a diameter of 20 cm. Find out the area of this circle.

Ans: For the circle, $d = 20$ $cm$.

Radius, $r = \frac{d}{2} = 10$ $cm$

Therefore, $A = \pi r^{2}$

$= 3.14 \times 10 \times 10 = 314$ $cm^{2}$

Area of the given circle is $314$ $cm^{2}$.

2. The height of a triangle is 10 cm and the base is 20 cm. What is the area of this triangle?

Ans: Area of the triangle $= \frac{1}{2} \times b \times h$

$= \frac{1}{2} \times 20 \times 10 = 100$ $cm^{2}$

Therefore, the area of the given triangle is $100$ $cm^{2}$.

3. The width of a rectangle is half of its length. The width is measured to be 10 cm. What is the area of the rectangle?

Ans: For the rectangle, $w = 10 cm$ and$ l = (10 \times 2) = 20$ $cm$.

Area of the rectangle, i.e., $A = l \times w$

$A = 20 \times 10 = 200$ $cm^{2}$

Therefore, the area of the given rectangle is $200$ $cm^{2}$. 

Example 4: What is the area of the following figure?

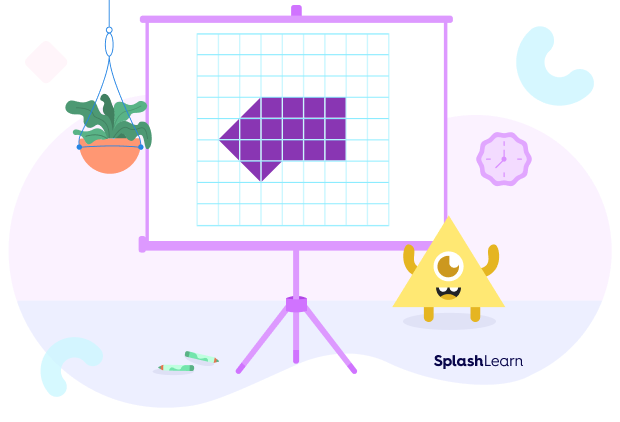
Solution:  Full square $= 1$ square unit

So, 14 full square $= 14$ square units

1 half square $= \frac{1}{2}$ square units

5 half squares $= 2.5$ square units

Total area $= 14 + 2.5 = 16.5$ square units. 

Example 5: What is the area of a rectangular park whose length and breadth are 30 m and 50 m respectively?

Solution: Given Data:

Length of the park $= 30$ m

Breadth of the park $= 50$ m 

Use the area formula.

Area of a Rectangle $= \text{Length} \times \text{Breadth}$

$= (30 \times 50)$ $m^{2}$ 

$= 1500$ $m^{2}$ 

Example 6: What is the area of a circular cricket stadium whose radius is 200 m?

Solution: Given data:

Radius of the cricket stadium $= 200$ m

Use the area formula.

Area of a Circle $= \pi r^{2}$

$= \pi \times 200 m \times 200 m$

$= 40000 \pi$ $m^{2}$

Example 7: What is the area of a square paddy field if each of its sides measures 10 units?

Solution: Given data:

Length of the side $= 10$ units 

Use the area formula.

Area of the square paddy field $= 10 \times 10$

$= 100$ square units

Practice Problems On Area

Frequently Asked Questions On Area