Composite Shape
A composite shape can be defines as a shape created with two or more basic shapes. We often refer to composite shapes as compound and complex shapes as well.
We see composite shapes every day. The shape of your curved bookcase, the mouse you are scrolling, and the bag you are carrying are all composite shapes.
Recommended Games
Examples of Composite Shapes
A range of shapes seen in our daily life are composite figures that can be made using two or more basic figures.
For example, here’s a composite shape:
Guess what this hexagon is made of? You guessed it right! Six triangles.
Here’s a composite shape formed by a rectangle and another smaller rectangle:

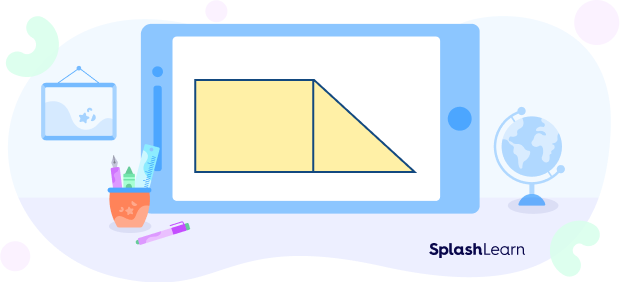
And another formed by a rectangle and a triangle:
Recommended Worksheets
Perimeter and Area of Composite Shapes
Imagine you are at a store, buying a rug with your parents. However, this is not just any rug; it is one that is customized according to your living room.
The process of calculating the perimeter and area of this customized rug is the same as calculating the perimeter and area of a composite shape.
Let’s explore how you can find the perimeter and area of composite shapes next!
Perimeter of Composite Shapes
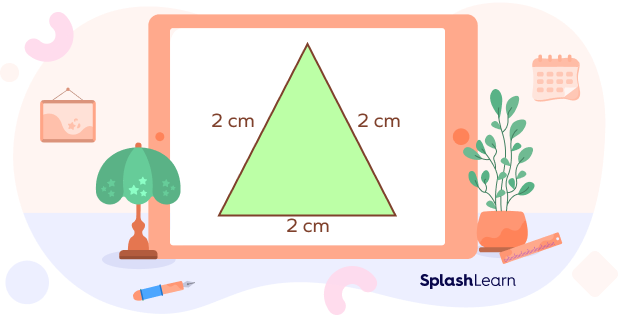
The perimeter of a shape is the outer length of the shape. If we have a triangle with each side that is 2 cm in length, then its perimeter is 6 cm.
Similarly, finding the perimeter of a composite shape means adding the length of the sides.
Let’s look at an example calculating the perimeter of a composite shape:
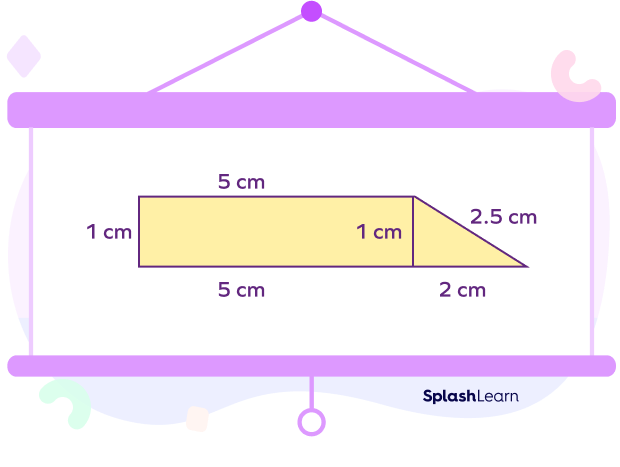
Starting from the left side, let’s add the length of every outer side to find the perimeter of this two-dimensional shape.
1 cm + 5 cm + 2.5 cm + 2 cm + 5 cm = 15.5 cm
We do not add the inner 1 cm, as the perimeter is the sum of all the outer sides of a composite shape. So, just remember that the perimeter is the addition of only the outer lining of the shape.
Area of Composite Shapes
The perimeter and area of composite shapes may be intertwined. We may often define the area of any shape through the perimeter, but these two are different concepts.
The perimeter simply traces the outer line of the shape, and the area calculates the space it holds. Hence, the area of any shape is the space that the shape encloses within its boundary or perimeter.
Finding the area of a composite shape involves calculating the area of different basic shapes.
So, what is the process of finding the area of these composite shapes, you ask?
The simplest way is to break the shape up:
- Divide the composite shape into basic shapes.
- Find the area of every basic shape separately.
- Now, add these areas to find the area of the composite shape.
With the help of these steps, let’s look at an example for finding the area of composite shapes.
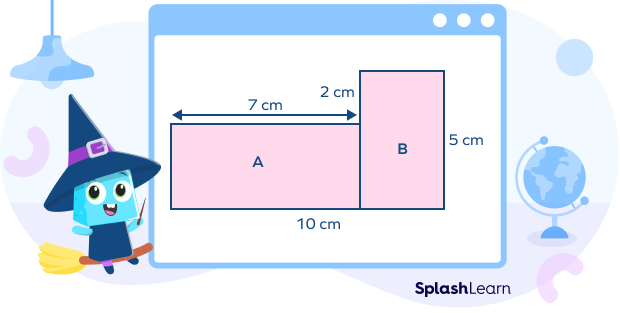
In the above composite shape, we have two basic shapes, A and B, both of which are rectangles. We have the length of a few sides defined in cm.
Let’s find the length of all the sides to proceed. We will mark vertices for the same:
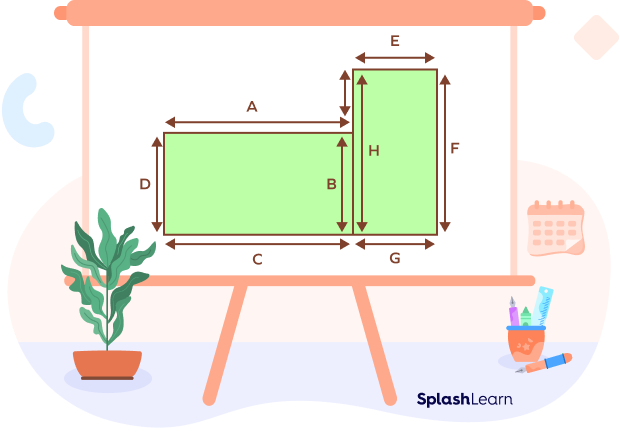
In the first rectangle, we know that A is 7 cm.
The height is not defined. But we have the height of H and the height of H-B. With this, we can say:
D or B = H – 2
= 3 cm
Now, similarly, we know F, but not the length G or E. However, we know the length of C + G and A.
This means that the length of the second rectangle can be:
G or E = (C + G) – A = 3 cm
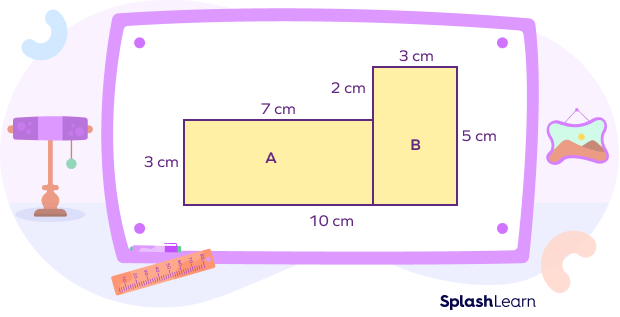
Area of the composite shape = Area of the First Rectangle + Area of the Second Rectangle
Area of the First Rectangle = 7 × 3
= 21 cm²
Area of the Second Rectangle
= 3 × 5
= 15 cm²
Area of the composite shape = 21 cm² + 15 cm²
= 36 cm²
Solved Examples
Example 1: If we need to find the area of the same composite shape but with a subtractive method, what will we do?
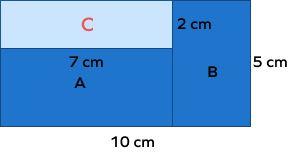
Solution: In the subtractive area method, we subtract the area instead of adding.
So, area of the composite shape = Area of the bigger rectangle – Area of C
Area of big rectangle = 10 × 5
= 50 cm²
Area of C = 7 × 2
= 14 cm²
Area of the composite shape = 50 cm² – 14 cm²
= 36 cm²
Example 2: How would we find the perimeter of the black shape?
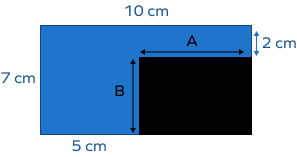
Solution: Let’s start by finding the length and height of the black rectangle:
Length of Side A = 10 – 5
= 5 cm
Length of the Side B = 7 – 2
= 5 cm
Perimeter of blue composite shape = 7 + 10 + 2 + 5 + 5 + 5
= 34 cm
Example 3: If we need to find out which of these three are two-dimensional composite shapes, how will we go about it?
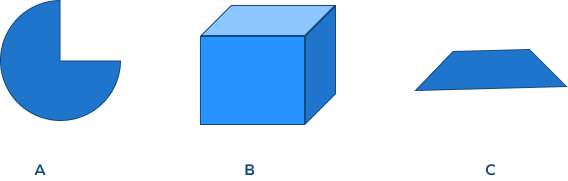
Solution: Going for the simplest one of all, we can clearly say that C is a composite shape. This is because the shape is created with one rectangle and two triangles.
Let’s talk about B. Do you think it is a composite shape?
It’s not. B is neither a 2D nor a 3D composite shape.
This can be a bit confusing; you may think we can make it with 3 rectangles, but it is actually a cube with 6 identical sides. So, this is a basic 3D shape, not a composite shape.
What about A, can we say it is a composite shape?
Yes, it is! Since it is a circle from which a triangle has been taken out, it is considered a composite shape.
Practice Problems
Composite Shapes - Definition With Examples
Find the area of the following composite shape:
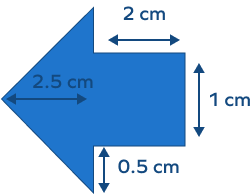
Area of the given shape = area of the triangle + the area of the rectangle
= 2.5 cm² + 2 cm²
Find the perimeter of the gray part in this composite shape:
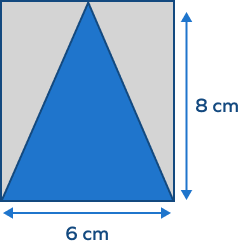
The perimeter of the rectangle is 28 cm, taking one side as 8 cm and the other as 6 cm.
Identify the 3D composite shape among the following shapes:

C is a composite shape made with a cube and cuboid.
Frequently Asked Questions
What is a composite figure?
A composite figure is the same as a composite shape. Any figure that we can break and form more than one basic shape from is called a composite figure.
Which formula can we use to find the area of a composite figure?
The area of a composite shape can be found by either adding or subtracting its basic shapes.
Therefore, we can use two formulas:
Area of Composite Shape (additive) = Area of Basic Shape A + Area of Basic Shape B + …
Area of Composite Shape (subtractive) = Area of Basic Shape A – Area of Basic Shape B – …
What is a composite solid figure?
A composite solid figure is a figure created with more than one solid, such as cylinders, cones, prisms, pyramids, etc.




































