What is Volume?
Every three-dimensional object occupies some space. This space is measured in terms of its volume. Volume is defined as the space occupied within the boundaries of an object in three-dimensional space. It is also known as the capacity of the object.
Finding the volume of an object can help us to determine the amount required to fill that object, like the amount of water needed to fill a bottle, an aquarium or a water tank.
Recommended Games
Volume of 3-Dimensional Shapes:
Since different three-dimensional objects have different shapes, their volumes are also variable. Let us look at some three-dimensional shapes and learn how to calculate their volume(V).
Sphere
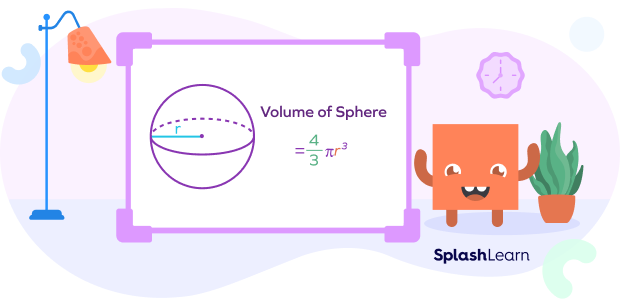
The simplest and most common type of three-dimensional shape is a sphere. Some examples of spheres that we see in daily life includes balls, globes, decorative lights, oranges, etc. The simplest measurement that can be made on a sphere is its radius. The volume of the sphere is calculated using its radius.
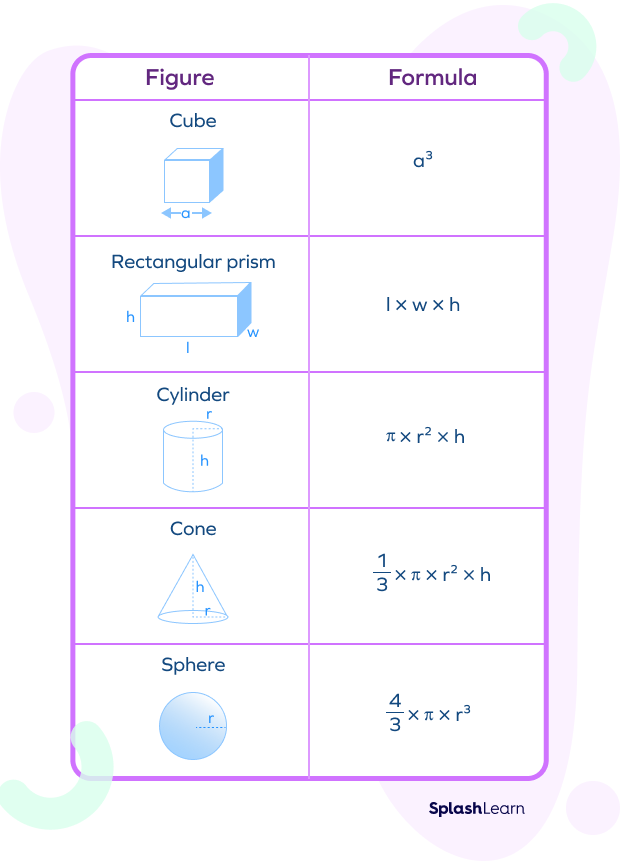
Volume of a Sphere = $\frac{4}{3}$πr3, where r is the radius of the sphere.
Cube
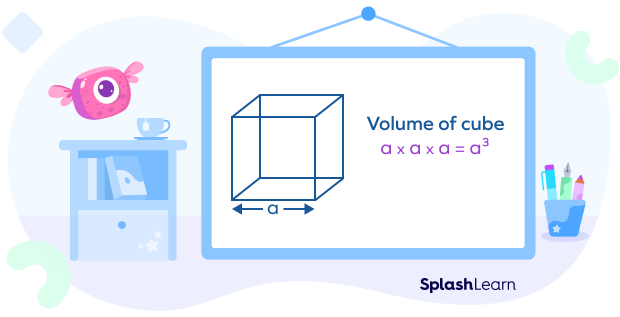
The next simple and common three-dimensional shape is the cube. It is identified by the unique property that each side of the cube is of the same length. Some everyday examples of objects in the shape of a cube are dice, Rubik’s cubes, sugar cubes, gift boxes, etc. The volume of a cube is calculated using the length of its side.
Volume of a Cube = a3, where a is the length of each side of the cube.
Cuboid
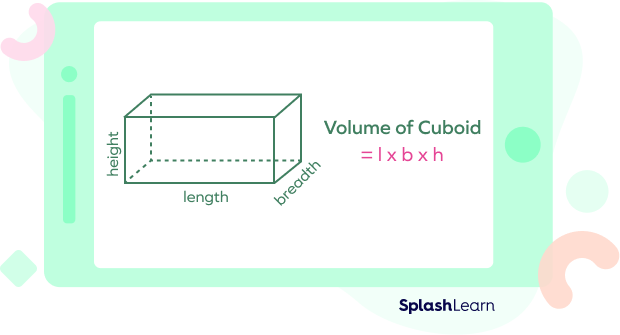
Cuboid shape is also referred to as the rectangular prism. In a cuboid, the length of the sides will vary. The following notation is used to represent the sides of a cuboid.
- Length = l
- Breadth = b
- Height = h
All these dimensions are used to calculate the volume of a cuboid. Common examples of cuboids are books, shoe boxes, bricks, mattresses, etc.
Volume of a Cuboid = l x b x h
Cylinder
A cylinder is also a three-dimensional shape with circular bases and a height separating the two bases. Everyday objects that are cylindrical include water bottles, buckets, candles, cans, etc. The volume of a cylinder is calculated by measuring the radius of the base and the height.
Volume of a Cylinder = πr2h, where r is the radius of the base, and h is the height of the cylinder.

Cone
A cone is a three-dimensional shape that we commonly see around us. An ice-cream cone, a party hat, a funnel, or a Christmas tree, all of these are examples of a cone. A cone is a distinctive three-dimensional geometric figure that has a flat surface and a curved surface, pointed towards the top.
Volume of a Cone = $\frac{1}{3}$πr2h, where r is the radius of the base of the cone, and h is the height of the cone from the base to the top.

Volume Measurement
Volume is calculated for three-dimensional objects and hence is represented in cubic units or another format of writing cubic unit; as this is commonly used (unit)³ such as cubic centimeters, cubic inch, cubic foot, cubic meter, etc If the length or radius is measured in centimeters, then the volume is measured in cubic centimeters (cm3). If the measurements are in meters, the volume is measured in cubic meters (m3).
When we measure the volume of liquids (for example, to find the volume of water that a cylindrical bottle can hold), we have to change the values in cm3 or m3 into liters. The volume can be converted from liters to centimeters using the following formula.
1 l = 1000 cm3
1 l = 1000 ml
1000 cm3 = 1000 ml
So, 1 cm3 = 1 ml
Conclusion
Understanding mathematical concepts like Volume becomes interesting with the help of visual aids like interactive games. You can check out games, worksheets and solved problems for topics like this on the Splashlearn website. Visit https://www.splashlearn.com/ to learn new concepts while having fun.
Solved Examples on Volume
1. Henry has a cylindrical water bottle with a base radius of 5 cm and a height of 10 cm. What is the volume of water that the bottle can store?
Solution:
Volume of the bottle= πr2h
= π (5 x 5) x 10
= π x 250
= 3.14 x 250
= 785 cm3
= 785 ml (1 cm3 = 1 ml)
2. Riaz owns a cricket ball with a radius of 3 cm. What is the volume occupied by the ball in Riaz’s bag?
Solution:
Volume of the ball = $\frac{4}{3}$πr3
= $\frac{4}{3}$ x $\frac{22}{7}$ x (3 x 3 x 3)
= 113.14 cm3
3. Conical Christmas tree is made using a clay. The height of the tree is 14 inches and diameter of the base is 6 inches. How much clay is used? (use π = $\frac{22}{7}$)
Solution:
Diameter = 6 inches
Radius = $\frac{6}{2}$ = 3 inches
Volume of the clay = $\frac{1}{3}$πr2h
= $\frac{1}{3}\times \frac{22}{7}\times 3\times 3\times 14$
= 132 cubic inches.
Practice Problems on Volume
Volume
Which of the following is the formula for the volume of a book with the dimensions l, b, and h?
A book is a cuboid whose volume is calculated using the formula l x b x h.
The volume of a traffic cone of height 20 cm and base radius of 10 cm can be calculated using which formula?
As a traffic cone is conical in shape, its volume can be calculated using the formula for the volume of a cone $\frac{1}{3}\pi$r$^2$h
What should be the volume of a box that can exactly fit 4 dice, each with a side of 3 cm?
A dice is in the shape of a cube. So, Volume of box = 4 cubes = 4 x $a^{3}$ = 4 x $(3)^{3}$ = 108 $cm^{3}$
What will be the volume of a football with a radius of 12 cm?
Volume = $\frac{4}{3}\pi r^{3}$ = $\frac{4}{3}\pi$ (12 x 12 x 12) = 7241.14 $cm^{3}$
Frequently Asked Questions on Volume
Is a volume of rectangular prism the same as a volume of cuboid?
Yes, a volume of rectangular prism is the same as a volume of cuboid. Cuboid has sides of unequal lengths. Its volume is calculated using the formula l x b x h, where l, b, and hare the different measurements of the shape.
How to calculate the volume of an irregular shape?
If you need to calculate the volume of a shape that is not one of the regular three-dimensional shapes, break up the irregular shape into different regular shapes. Add the individual volumes of these shapes to get the overall volume.
What is the easiest way to understand volume?
Volume is the space occupied by any object. This space occupied depends on the shape of the object. The best way to understand is by examining different objects and finding the volume occupied by them.
What should be kept in mind when calculating the volumes of different shapes?
An important check before calculating the volume of any shape should be that all measurements are in the same unit. If one measurement is provided in cm and the other in m, convert both into cm or m before calculating the volume.
























