A wide range of geometry deals in flat shapes that you can draw on a piece of paper, such as squares, circles, and triangles. Solid geometry deals with three-dimensional solid shapes that exist around us, such as spheres, cones, and cubes. The outer layer of an object we see around us is called the surface of an object. It has an area but no thickness. For example, the surface of a mirror is smooth. These solids have either flat or curved surfaces.
The surface of walls, floor, top of a table, or paper are examples of flat surfaces. And the surface of balls, eggs, or lemons is curved. Observe the examples of flat and curved surfaces in the figure below.
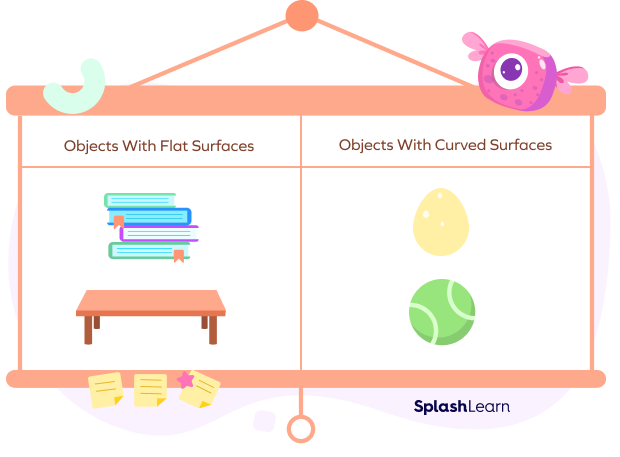
Let’s explore the definition of flat surfaces and more.
What is a Flat Surface in Geometry?
In geometry, a flat surface is also called a plane. Plane geometry deals in flat shapes that you can draw on a piece of paper, such as squares, circles, and triangles. A plane or flat figure has two dimensions: length and width.
A solid or 3D shape is a shape that takes up space. The outer layer of a solid is called the surface of the solid. When the surface of a solid is a plane surface with no depths, in other words, flat, it is called a flat surface. We see many flat things in our surroundings every day. For instance, the surface of a book, table, or dresser can be flat.
Recommended Games
Basic Terms of Solid or 3D Shapes
A solid or 3D shape is a shape that takes up space. They consist of 3 dimensions, namely length, breadth, and height. They are all the things that we can hold. They are found in our day-to-day life. For example, your books and football are solid shapes.
Some features are standard across all the 3D shapes. These features include faces, edges, and vertices or corners.
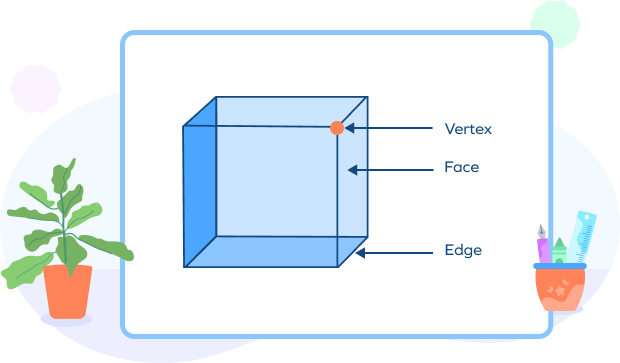
The surface of a solid, which are flat, is also called the face of the solid. The face of a solid can be any flat shape, such as squares, circles, triangles, and so on. An edge is the line segment where two faces of the solid meet. Two or more edges meet at a point called the vertex. A solid shape can have one or multiple surfaces. Let’s study the different types of surfaces a solid shape can have.
Recommended Worksheets
Different Types of Surfaces
There are mainly two types of surfaces in a 3D shape: flat and curved surfaces.
As the name suggests, the surfaces of a solid that are flat or plane are called flat surfaces. On the other hand, curved surfaces are rounded surfaces that are not flat. For example, a cone has one flat surface and a curved surface, as shown in the figure below.
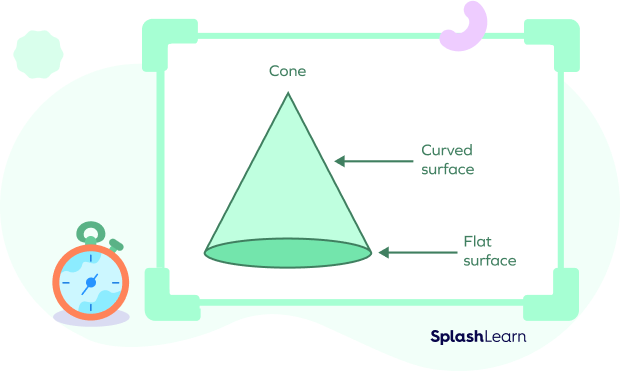
How to Identify Flat Surfaces in 3D Shapes
As we have read in the previous section, the surface of a solid can be flat or curved. The plane surface of a 3D shape is a plane figure, such as squares, circles, triangles, etc.
If we observe some 3D cubes, cuboids, pyramids, and prisms, we’ll see that they consist of only flat or plane surfaces. 3D figures or shapes, like a cylinder or cone, are made of both flat and curved surfaces. Also, specific 3D shapes, like spheres, have no plane surfaces; they only have one curved surface. You can slide an object that has a plane surface. If an object has a curved surface, then you can roll them along its curved surface.

A cube has six faces, which are identical squares. A cylinder has a curved surface and two equal circles as plane surfaces. A sphere is made of one curved surface.
The Number of Flat Surfaces in Various 3D Solids
Look at the figure below. How many plane surfaces can you see?
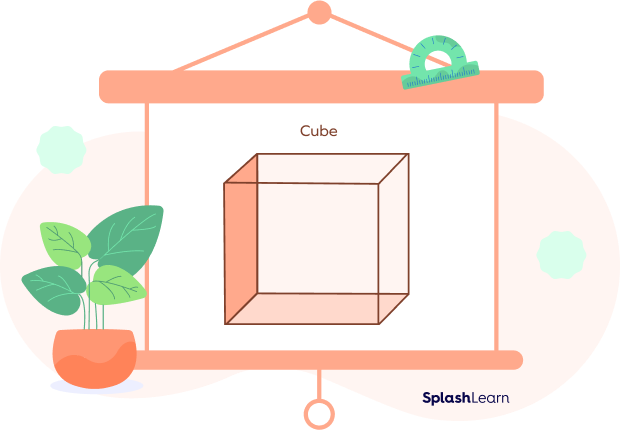
The above figure is a cube with 6 plane surfaces or faces. Each face is a square. It has one face each on the top, bottom, front, back, and left and right sides.
The surfaces of some common solids are listed below:
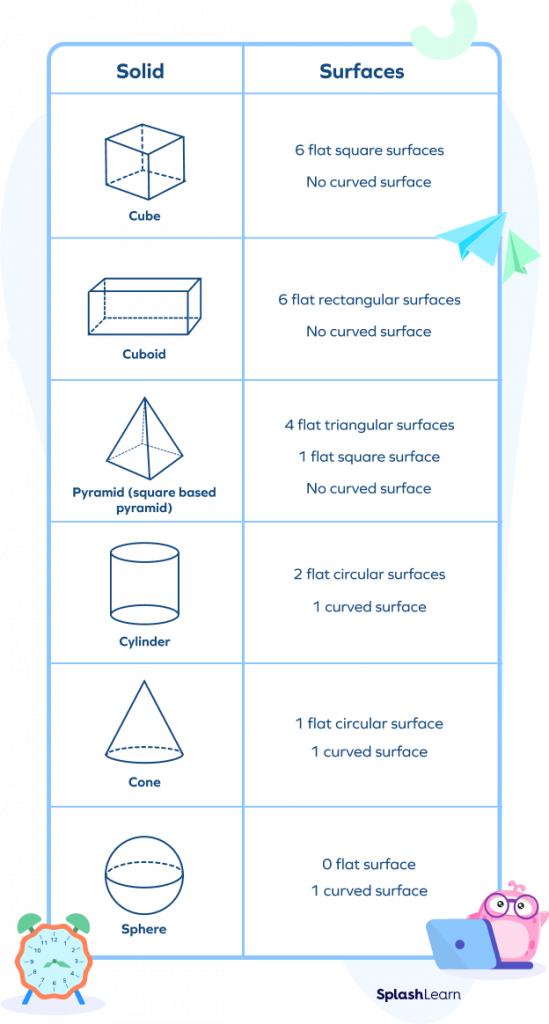
Surface Area of 3D Shapes
The surface area of a solid is the sum of the areas of each face. When finding the surface area of 3D figures, consider it as unfolding the shape or flattening it out. Then find the area of each plane surface.
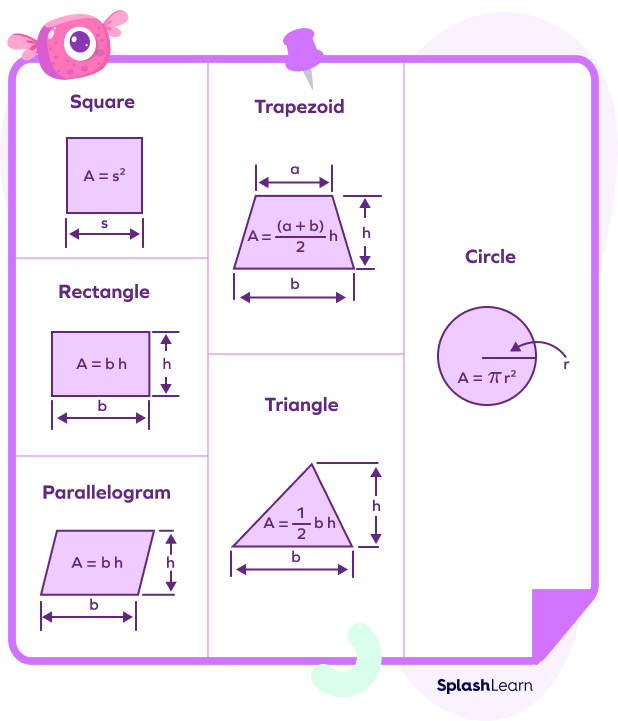
The plane surfaces of a solid shape are basic 2D shapes, like squares, rectangles, triangles, parallelograms, circles, and so on. So, to find the surface area of a solid, we must know the area of the basic flat shapes. Here is a list of basic shapes and their area:
Solved Examples
Example 1: How many faces does the following 3D shape have?
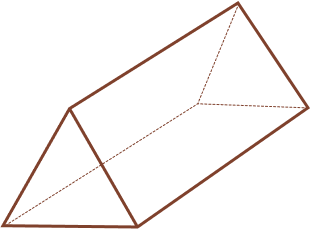
Solution:
The flat or plane surfaces of a solid shape are called faces. The figure is a triangular prism. It has 2 triangular and 3 rectangular faces. So there are 5 faces in the 3D figure.
Example 2: What is the shape of each flat surface of a cylinder?
Solution:
A cuboid has two flat or plane surfaces that are circular.
Example 3: Each side of a cube measures 5 cm. Find the total area of its surfaces.
Solution:
A cube has 6 flat square surfaces. Each side of a cube measures 5 cm, and then the area of each surface is $($5$ \text{cm})^2$ $= 25$ cm².
Therefore, the total surface area of a cube $= 6 \times 25$ cm²$ = 150$ cm²
Practice Problems
Flat Surface - Definition with Examples
Which of the following shapes have only flat surfaces?
A cuboid has 6 flat or plane surfaces and no curved surface. Cylinders and cones have at least one curved surface, while a sphere has all curved surfaces.
Which of the following 3D shapes have 1 flat and 1 curved surface?
A cone has one flat and one curved surface. A cylinder has two flat surfaces. A sphere has all curved surfaces, and all the surfaces of a pyramid are flat.
The flat surface of a solid is called __________?
The flat or plane surface of a solid is called a face.
Frequently Asked Questions
What is the difference between the surface area and volume of a cube?
The surface area of a cube is the region occupied by the cube’s surface, whereas the volume is the measurement of space available in the cube.
The surface area of a cube $= 6 \times $(length)$^2$
The volume of a cube $=$ length$^2$
Are polygons flat?
Yes, polygons are two-dimensional closed-plane shapes with straight sides. All the plane shapes are flat.
Is the plane a flat surface?
Yes, a plane is a flat, two-dimensional surface. It extends infinitely in every direction.






















