Cubic Units

What is a Cubic Unit?

A cubic unit is a unit used to measure volume.

In other words, these units are a way of measuring the space that is occupied by something.

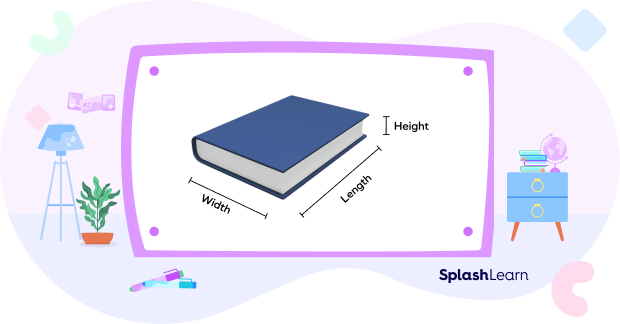
Think of a book: What is its volume? Its volume depends on its length, width, and height. Multiplying these three linear measurements gives us a cubic measurement.

Volume refers to the space occupied by an object or a three-dimensional figure. It is measured in cubic units.

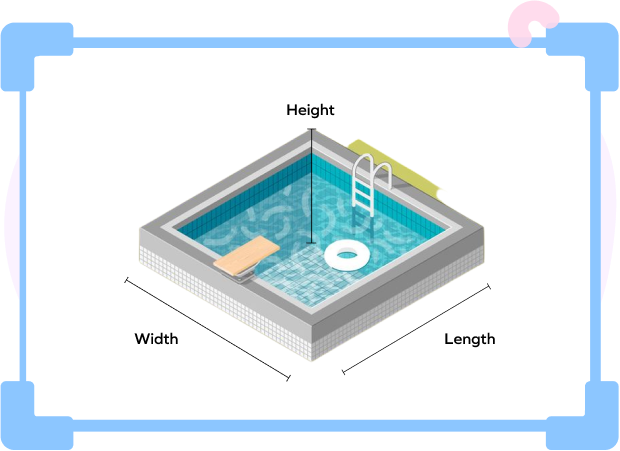
Similarly, the volume of water in a swimming pool can be measured in terms of cubic units. 

Cubic Unit Definition

In geometry, cubic units can be defined as the units used to measure volume. The volume of a unit cube whose length, width, and height are 1 unit each is 1 cubic unit. 

Cubic units symbol can be given as unit³. For example, ‘cubic centimeter’ can be represented as cm³.

Regular measurement units, like inches, feet, yards, miles, centimeters, meters, and kilometers, describe the sides of a shape, like the sides of a rectangle. Cubic units measure three-dimensional space or volume. 

How Does a Cubic Unit Work?

Each dimension of a unit cube (length, width, and height) is one unit.

So, one unit of length with one unit of width and one unit of height together make a volume of one cubic unit.

When we measure volume, we measure it in terms of how many ‘unit cubes’ of 1 cubic unit volume each will fit into that volume if we place them side by side or one on top of another. 

In the image below, we can find the volume of the given figure by counting the total number of cubic units. It is made up of $10 \times 10$ cubic units. So the volume of the figure is 100 cubic units. 

When calculating the volume of something in cubic units, you have to multiply the value of each dimension (length, width, and height). 

The length, width, and height are measured in single units like inches, feet, and yards or centimeters and meters.

For example, in the figure given below, the cuboid is made up of smaller unit cubes. The cuboid has a length of 6 inches, a height of 4 inches, and a width of 2 inches.

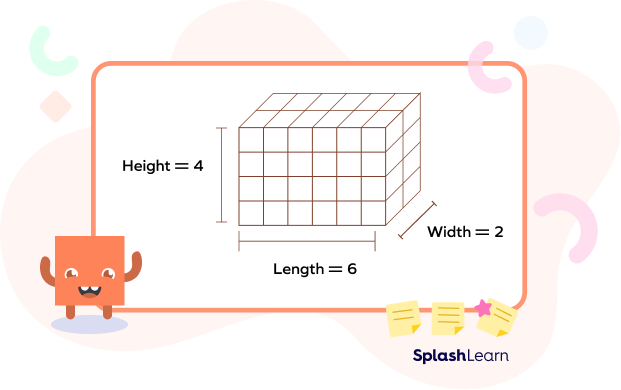
When you multiply the dimensions, the value you get is the volume, which will be in terms of cubic units (like cubic inches, cubic feet, cubic yards, cubic centimeters, or cubic meters). 

Multiplying the dimensions of the cuboid:

$6$ $\text{inches} \times 4$ $\text{inches} \times 2$ $\text{inches} = 48$ $\text{cubic inches}$

48 cubic inches is the volume in cubic units. 

The length, width, and height of the cuboid can also be measured by counting the number of unit cubes. The volume is then determined in cubic units. 

Let us try another example. If a cube has a side of 5 inches, what will be its volume? 

Volume of a cube $= \text{length} \times \text{width} \times \text{height}$ 

Since the length, width, and height are equal in a cube, the volume will be:

$5 \times 5 \times 5 = 125$ cubic inches. 

We can see that the unit of inches changes to cubic inches. 

Some examples of cubic units in metric units are cubic meters and cubic centimeters, and in customary units are cubic inches and cubic feet. 

Units like square inches, square feet, square yards, square miles, square centimeters, square meters, and square kilometers describe the area of a shape and are used to measure two-dimensional shapes or areas.

Cubic units like cubic inches, cubic feet, cubic centimeters, and cubic meters measure three-dimensional space or volume.

Cubic Conversions

We can convert one cubic unit (such as cubic inches) to another cubic unit (such as cubic feet). 

Some approximate conversions for cubic units are given below: 

1 cubic inch $= 0.0006$ cubic feet 

1 cubic inch $= 0.00002$ cubic yards 

1 cubic inch $= 16.39$ cubic centimeters 

1 cubic inch $= 0.000016$ cubic meters 

1 cubic foot $= 1728$ cubic inches  

1 cubic foot $= 0.037$ cubic yards 

1 cubic foot $= 28316.85$ cubic centimeters 

1 cubic foot $= 0.028$ cubic meters 

1 cubic centimeter $= 0.000001$ cubic meters 

1 cubic centimeter $= 0.061$ cubic inches 

1 cubic centimeter $= 0.000035$ cubic feet

1 cubic centimeter $= 0.000001$ cubic yards

1 cubic meter $= 1,000,000$ cubic centimeters

1 cubic meter $= 61023.7$ cubic inches 

1 cubic meter $= 35.3$ cubic feet 

1 cubic meter $= 1.31$ cubic yards

Solved Examples

1. How much does each side of a unit cube measure? 

Solution: 1 unit. A unit cube has a length, width, and height of one unit each. 

2. A book has a length of 12 inches, a width of 10 inches, and a height of 4 inches. What is its volume? 

Solution: Volume of the book $= \text{length} \times \text{width} \times \text{height}$

$= 12$ $\text{inches} \times 10$ $\text{inches} \times 4$ $\text{inches}$

$= 480$ cubic inches

The volume of the book is 480 cubic inches. 

3. How many cubic inches make one cubic foot?  

Solution: 1 foot $= 12$ inches 

1 cubic foot $= 1$ $\text{foot} \times 1$ $\text{foot} \times 1$ $\text{foot}$

So 1 cubic foot $= 12$ $\text{inches} \times 12$ $\text{inches} \times 12$ $\text{inches}$

$= 1728$ cubic inches

Practice Problems

Frequently Asked Questions