Unit Cube

Unit Cube: Introduction

Unit cube is a cube with the side length of 1 unit.

A cube is a three-dimensional square. It is an object with all edges equal in size. A cube has 12 edges. Thus, a unit cube has 12 edges, all measuring 1 unit.

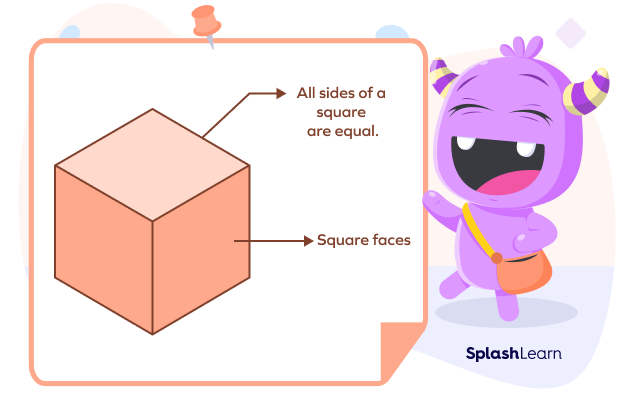
But the question is what a unit cube is in math. In this article, this is the question we will be answering.

What Is a Unit Cube in Math?

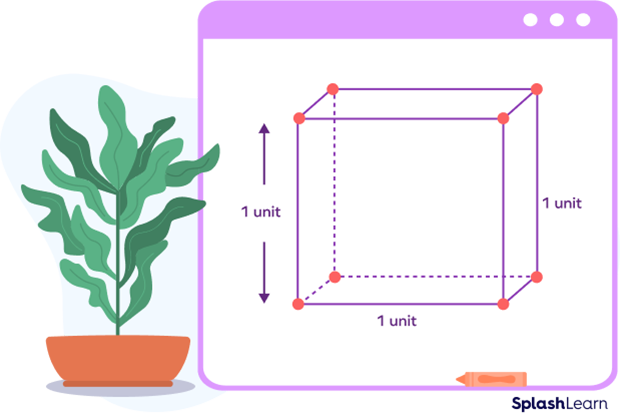
In geometry, a unit cube is a cube where each side is 1 unit long.

Unit Cube Definition

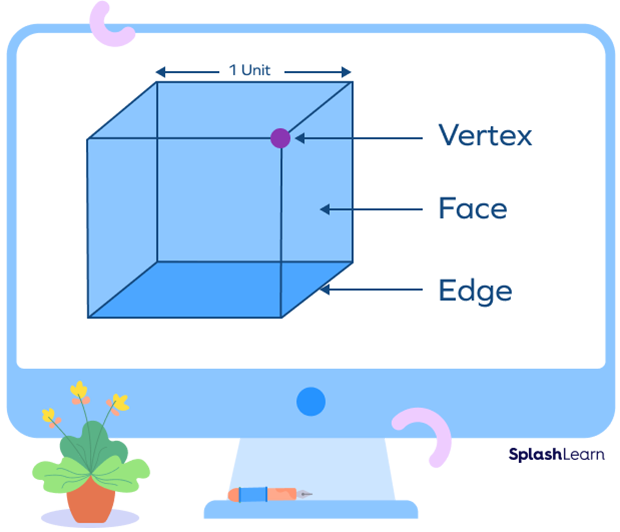
A unit cube is a cube where each side measures 1 unit. 

It has 8 vertices, 12 edges, and 6 faces.

What Is the Volume of a Unit Cube?

The amount of space something occupies is called its volume. 

Volume of a cube $=  side^{3}$

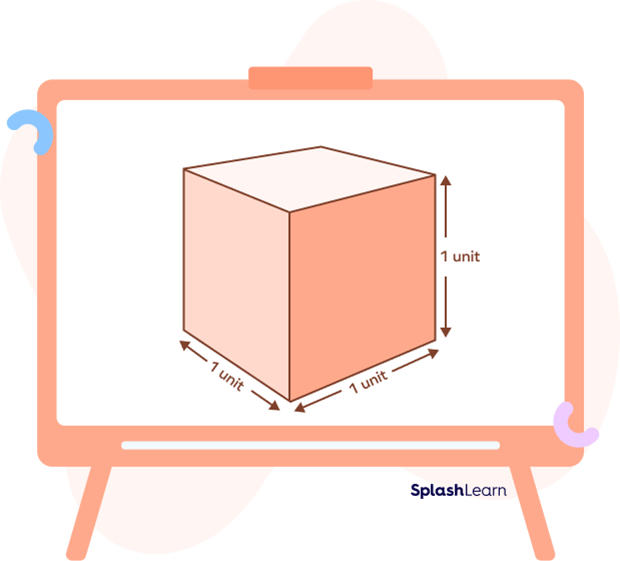
All the sides of a cube are the same length. 

All the sides of a unit cube have the length of 1 unit. So, 

Volume of a unit cube $= Side \times Side \times Side$

     $=1\; unit \times 1\; unit \times 1\; unit$

     $=1\; cubic\; unit$

     $= 1\;unit^{3}$

How to Find the Volume of a Unit Cube?

If a solid shape is made using unit cubes, the volume of the shape is equal to the number of unit cubes that make up the shape.

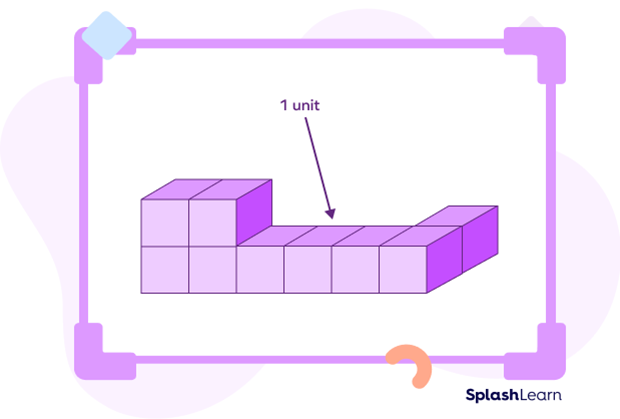
Example: The given solid shape is made of 9 unit cubes. 

Volume of each unit cube $= 1\; unit^{3}$

Therefore, its volume is $6\; unit^{3}$. 

Volume of Unit Cube Formula

The formula to find the volume of any type of cube is given by

Volume $= Side \times Side \times Side = Side^{3}$

For a unit cube, the length of the side is 1 unit.

Volume $= 1\; unit \times 1\; unit \times 1\; unit = 1\; unit^{3} =$ 1 cubic unit

Volume of Unit Cube Using Side Formula

The volume of a cube can be found by multiplying the length of the edge three times.

For example, if the length of an edge of a cube is 5, the volume will be $5^{3}$. The formula to calculate the volume of a cube is given as,

Volume of a cube $= side^{3}$.

Volume of Unit Cube Using Diagonal Formula

The volume of the cube can also be calculated if the diagonal is known to us.

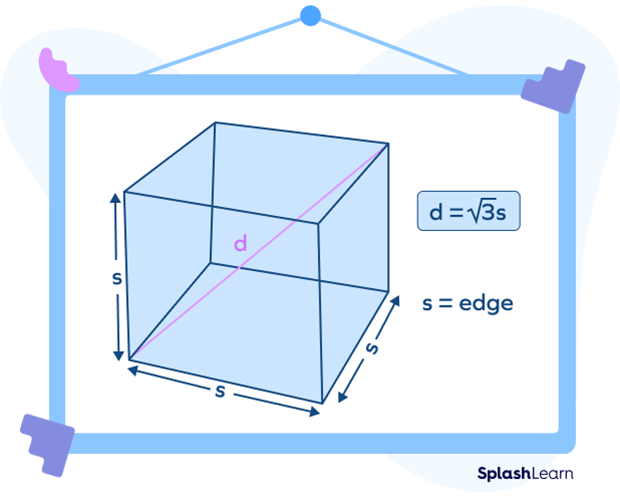
The diagonal of a cube is given by the formula

$d = \sqrt{3} \times s$, 

where “s” is the length of the side of the cube. 

From this formula, we can write the side length “s” as, $s = \frac{diagonal}{\sqrt{3}}$.

Thus, the volume of a cube equation using diagonal can finally be written as:

Volume of the cube $= s^{3} = \frac{\sqrt{3} \times d^{3}}{9}$

where d is the length of the diagonal of the cube.

What Is a Unit Cube and What Is Its Purpose?

A unit cube is a cube where each side is 1 unit long. 

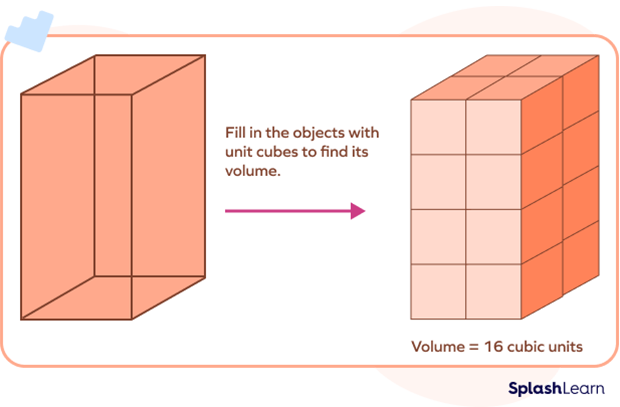
Unit cube can be used to find the volume of a solid shape. If a solid shape is made of n unit cubes, each having a volume of $1\; unit^{3}$, then the volume of the given solid shape is “n” $unit^{3}$. The number of unit cubes that fit in the object is the volume of the object. 

Let’s see an example of unit cubes forming a solid shape such that the number of unit cubes defines the volume of the solid.

Surface Area of a Unit Cube: Introduction and Formula

The total area that the surface of a three-dimensional object would cover if its sides were laid flat is called its surface area. Surface area is measured in square units.

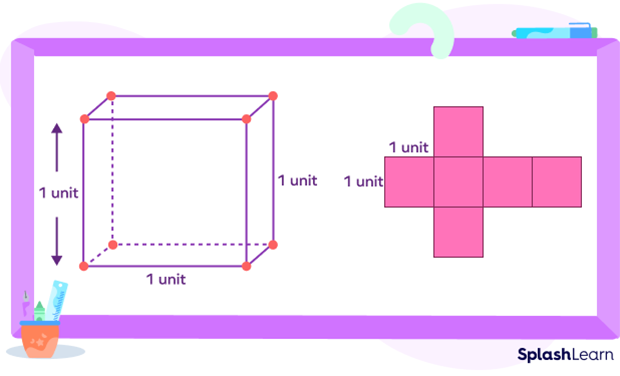
A cube has 6 square faces. A unit cube has 6 square faces with each side 1 unit long. 

So, the area of each side of the cube $= 1\; unit \times 1\; unit = 1\; \text{square unit}$

The surface area of a unit cube $= 6 \times area\; of\; one\; face$

         $= 6 \times 1\; square\; unit$

         $= 6\; square\; units$

Therefore, the surface area of a unit cube is 6 square units.

Are Unit Cubes and Volume the Same?

No, unit cubes and volume are not the same although they refer to the same thing. Volume is a property of a shape whereas unit cube is the measure of that quantity. 

For example, when we say length and 1 meter, they both refer to almost the same object, but there are subtle differences. 

Why Is Volume Calculated in Cubic Units?

Volume of a cube $= Side \times Side \times Side$

Volume is the multiplication of 3 similar kinds of quantities, so when we multiply a unit, let us say “meter”, thrice, we get

$meter \times meter \times meter = meter^{3}$

Hence, we can say that volume is calculated in cubic units or $unit^{3}$.

Fun Facts on Unit Cube

1. A unit cube can be used to measure the volume of other objects or solids.

2. To find the volume of objects using unit cubes, fill the object with unit cubes. 

3. The number of unit cubes that fit in the object is the volume of the object. 

4. A Rubik’s Cube is made up of 27 small cubes.

Conclusion

In this article, we learned about cube, unit cube, its volume, surface area, and other related topics. Now we can look at some examples and practice solving problems to master the concept!

Solved Examples on Unit Cube

1.  What is the volume of an object that is made up of combining the eight unit cubes?

Solution:

The new shape is made by combining the eight unit cubes. 

We know that the volume of a unit cube is $1\; unit^{3}$. 

Therefore, the volume of the new object $= 8 \times 1\;  unit^{3} = 8\;  unit^{3}$

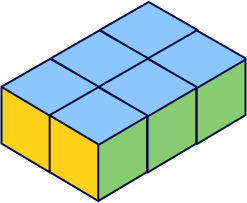
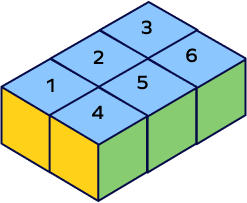
2. What is the volume of the given solid shape composed of unit cubes?

Solution:

Let’s count the number of unit cubes that form the given solid shape.

There are 6 unit cubes fitting perfectly in the shape. 

Volume of each unit cube is $1\; unit^{3}$.

So, volume of the given solid $= 6\; unit^{3}$

3. Using the volume of a cube formula, calculate the side length of a Rubik’s cube whose volume is $8\; in^{3}$.

Solution: 

Volume of Rubik’s cube $= 8\; in^{3}$

Using the volume of cube formula,

Volume of the cube $= side^{3}$ , where “s” is the side length.

Putting the values, we get,

$\Rightarrow 8 = (side^{3})$

Hence, side length of the Rubik’s cube $= 2\; in$.

4. Find the volume of a cube if the length of its diagonal is 3 inches?

Solution: 

To find: Volume of cube

Given: Diagonal of the cube $= 3\; in$.

Using the volume of a cube formula,

The volume of the cube when diagonal is given is:

Volume of cube $= \frac{\sqrt{3} \times d^{3}}{9}$ 

$\Rightarrow$ Volume of given cube $= \frac{\sqrt{3} \times 3^{3}}{9} = 3\sqrt{3}\; in^{3}$

5.  Find the volume of a cube if the length of its side is 7 feet?

Solution: 

Side of the cube $= 7\; feet$

Volume of cube $= side^{3}$

$\Rightarrow$ Volume of given cube $= 7^{3} = 343$ square feet

Practice Problems on Unit Cube

Frequently Asked Questions on Unit Cube