Cones can be found in a variety of things we see every day. An ice cream cone, a traffic cone, and a birthday cap are just some common examples of the shape of a cone.

Despite them being so abundantly present in our everyday lives, we might still fail to understand the fundamentals of cones in geometry.
To help you understand the wonder of cones, we have prepared a guide that takes you through all the basics. Let’s begin!
What Is a Cone in Math?
In maths, a cone is defined as a distinctive three-dimensional geometric figure with a flat and curved surface pointed towards the top. The term “cone” is derived from the Greek word “konos”, which means a wedge or a peak. The pointed end is the apex, whereas the flat surface is called the base.
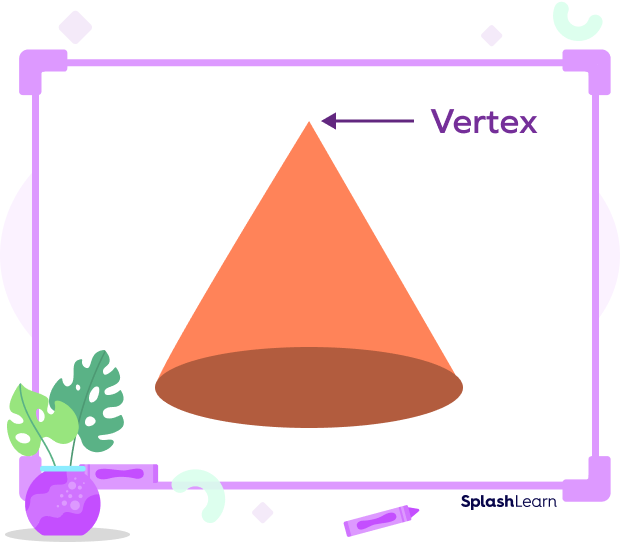
The three main properties of a cone are:
- It has one circular face.
- It has zero edges.
- It has one vertex (corner).
Recommended Games
What Are the Elements of a Cone?
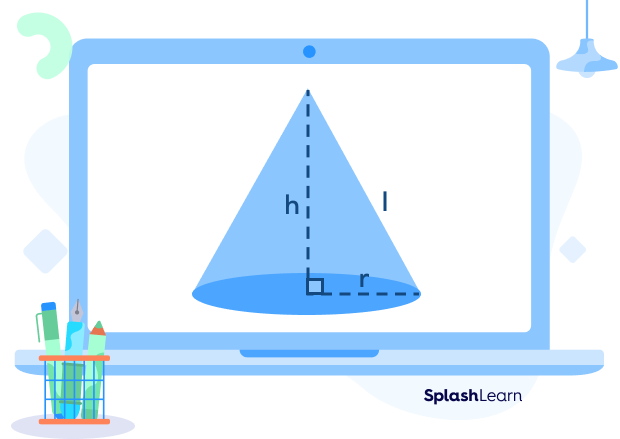
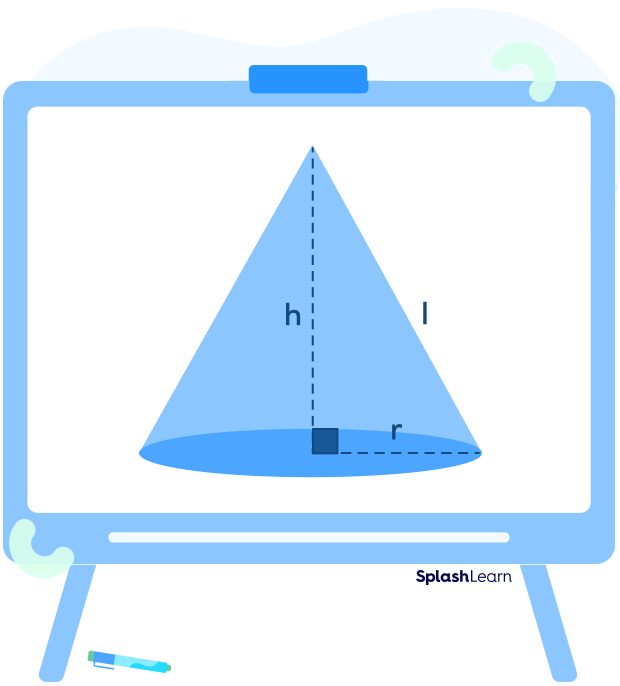
The three main elements of a cone are its radius, height, and slant height.
Radius of the Cone
Radius is defined as the distance between the center of the circular base to any point on the circumference of the base.
Height of the Cone
The height is the distance between the apex of the cone to the center of the circular base.
Slant Height of the Cone
The slant height of the cone is the distance from the top of the cone to the point on the outer edge of the circular base. The formula for the slant height is derived using the Pythagorean theorem.
Here, l is the slant height of the cone, r is the radius, and h is the height of the cone.
Recommended Worksheets
Types of Cones
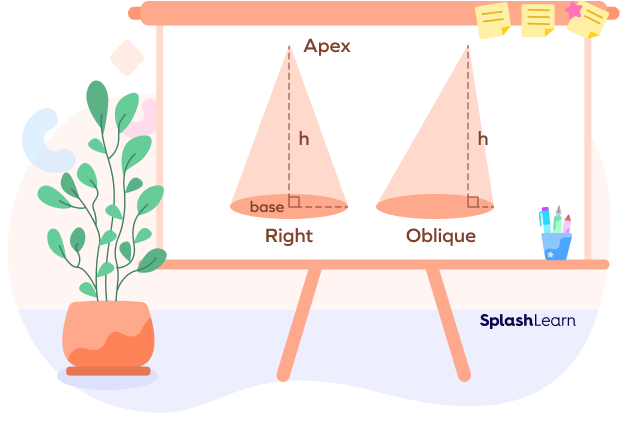
While studying cones in geometry, we generally consider the right circular one. But a cone can be of two categories, depending upon the position of the vertex on the base:
- A right circular cone is one whose apex is perpendicular to the base. Here, the axis makes a right angle.
- If the vertex position is anywhere besides the center of the base, it is an oblique cone. Here, the axis is non-perpendicular.
Some Fun Facts about Cones
1. The cone and pyramid are related. Their surface area formulas are also similar!
2. Our eyes have 6–7 million cones to help them adjust to color sensitivity.
Formulas Related to a Cone
A cone is formed by using a set of lines that connects to a single point called the vertex.
Let’s explore the different formulas related to a cone that will help you solve some interesting problems in the future.
Curved Surface Area of a Cone
A cone has both flat and curved surface areas. When we talk about the curved surface area of a cone, it refers to the area of the curved part of the cone only, not the circular base.
The curved surface area of a cone is given by the formula:
Curved Surface Area = π ✕ r ✕ l square units,
where r = radius of the base of the cone, l = slant height of the cone, and π = 3.14
Total Surface Area of a Cone
The total surface area of a cone is the sum area of its circular base and the curved surface.
The curved surface area of a cone is given by the formula:
Total surface area = Area of Curved Surface + Area of Circular Base
TSA = π ✕ r ✕ l + π ✕ r²
or, TSA= π ✕ r ✕ (l + r) square units.
Volume of a Cone
The volume of a cone in geometry is the amount of the space that the cone occupies. The volume of a cone can also be defined as the capacity of a liquid that a cone can hold if it were hollow from the inside. As the cone has a circular base, we can easily calculate the volume of the cone by measuring the radius “r”, and the height “h”.
V = $\frac{1}{3}$ ✕ (π ✕ r² ✕ h) cubic unit.
Solved Examples on Cone
Example 1: Find the volume of a cone where r = 5 cm and h = 7 cm.
Solution: By using the formula for the volume of a cone, we get:
V = (1/3)πr² h
Here, r = 5 cm, h = 7 cm
V= $\frac{1}{3}$ ✕ 3.14 ✕ 5 ✕ 5 ✕ 7
= $\frac{1}{3}$ ✕ 549.5 = 183.16 cm³
Example 2: Calculate the curved surface area of a cone where the radius of the base is 8 cm and slant height is 24 cm.
Solution: We can find the curved surface area of the cone by using the formula,
Curved Surface Area = π ✕ r ✕ l
Here, r = 8 cm, l = 24 cm
Therefore,
Curved surface area of the given cone = 3.14 ✕ 8 ✕ 24 = 602.88 cm².
Example 3: If the slant height of a cone is 25 cm, and its radius is 7.5 cm, find the total surface area of the cone.
Solution:
The total surface area of a cone is given by,
Total Surface Area = π ✕ r ✕ (l + r)
Here, r = 7.5 cm, and l = 25 cm.
Therefore,
Total surface area of given cone = 3.14 ✕ 7.5 ✕ (7.5 + 25)
= 23.55 ✕ (32.5)
= 765.37 cm²
Practice Problems on Cone
Cone - Definition With Examples
Find the volume of a cone where the radius is 8 cm and height is 13 cm.
By using the formula for the volume of a cone, we get:
V = (1/3) πr² h
Here, r = 8 cm, h = 13 cm
V= $\frac{1}{3}$ ✕ 3.14 ✕ 8 ✕ 8 ✕ 13
= $\frac{1}{3}$ ✕ 2612.48 = 870.82 cm³
The slant height of a cone is 21 cm, and its radius is 12 cm. Find the total surface area of the cone.
The total surface area of the cone is given by,
Total Surface Area= π ✕ r ✕ (l + r)
Here, r = 12 cm, and l = 21 cm.
Therefore,
Total surface area of given cone = 3.14 ✕ 12 ✕ (12 + 21)
= 37.68 ✕ 33
= 1243.44 cm²
Find the curved surface area of a cone where r = 10 cm, and slant height is 21 cm.
We can find the curved surface area of the cone by using the formula,
Curved Surface Area = π ✕ r ✕ l
Here, r = 10 cm, l = 21 cm
Therefore,
Curved surface area of the given cone = 3.14 ✕ 10 ✕ 21 = 659.4 cm².
Frequently Asked Questions on Cone
How many faces and vertices does a cone have?
A cone has one face with one vertex. The pointed top or the vertex of the cone is also called its vertex.
What are some real-life examples of a cone?
Cones are present around us everywhere. The hats that we use at parties, the Christmas tree we see during holiday festivities, or sometimes, even the carrots we eat are real-life examples of a cone.
What is the difference between a cone and a triangle?
A cone is a 3-D geometric figure with a circular base and a pointed edge. A triangle, on the other hand, is a 2-D figure that has three edges and vertices.


















