What Is the Volume of a Cube?
A cube is a three dimensional solid with six square faces of the same length. The total space occupied by a cube is called its volume. If we have a cube, and we fill it with water, the amount of water that fits inside the cube is called its volume.

Recommended Games
Examples of Volume of a Cube from Everyday Life
- If we fill a cardboard box with confetti balls, the amount of confetti balls that will fit in the cardboard box shows its volume.
- If we fill a cubical aquarium with water, the amount of water filled inside is its volume.

Recommended Worksheets
What Is the Volume of a Cube?
Just like the area is the amount of space occupied by a two-dimensional object, volume is defined as the space occupied by a three-dimensional object.
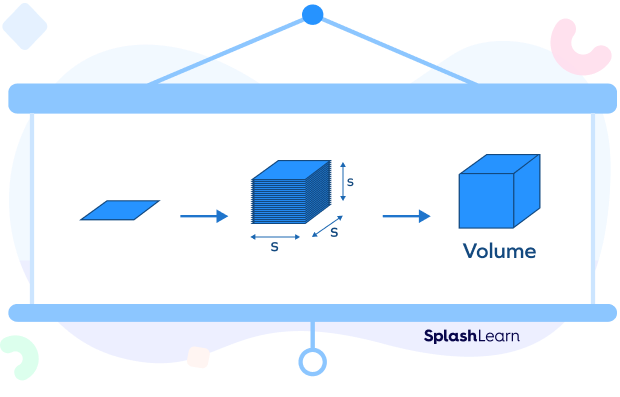
Consider a square sheet of paper with sides s. Its area will be s²; now if we stack them one over the other up to height s, then the volume of the cube can be found by multiplying the base area (s²) with the height (s).
Thus, the volume of a cube = s² ✕ s = s³
The volume of a cube can also be found by the number of cubic units required to fill the cube completely.
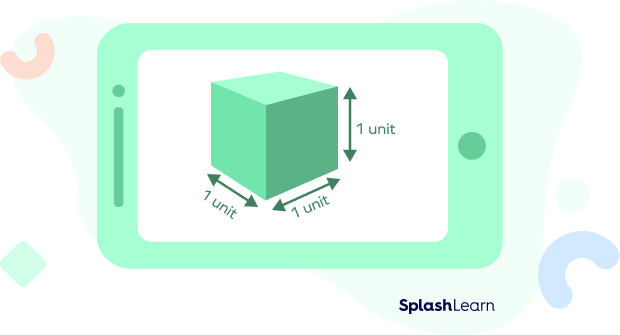
A unit cube has all its sides of length 1 unit.
So, the volume of unit cube = 1 unit ✕ 1 unit ✕ 1 unit = 1 cubic unit.
Now let’s find the volume of a cube with side = 4 units.

The volume of the cube will be equal to the number of unit cubes that make up the cube.
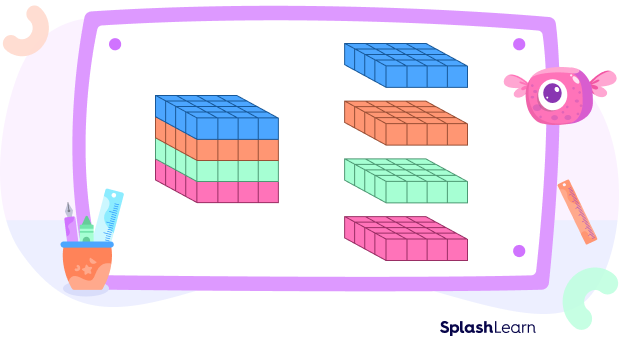
Each row has 16 cubes.
The cube of side 4 units is made up of 64 unit cubes. Therefore, its volume is 64 cubic units.
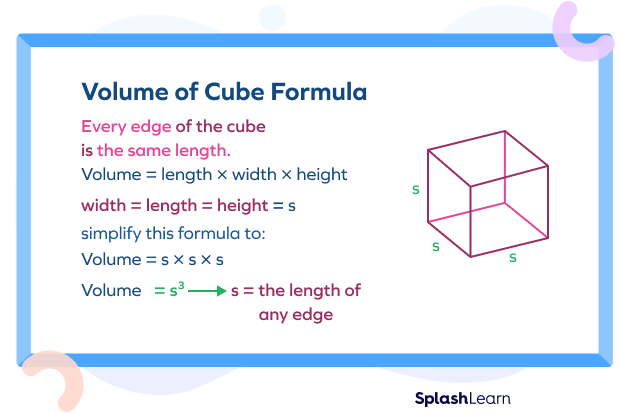
Volume of a Cube Formula
To find the volume of a cube, we need to know the length of any one edge of the cube. The length is to be multiplied by itself three times to get the volume.
The volume is measured in cubic units. For example, cubic meters (m3), cubic centimeters (cm3), etc.
For example, if the length of an edge is known to be 6 cm, then the volume of the cube will be 6 × 6 × 6 = 216 and the unit will be cm3 ; here, the volume of the cube is 216 cm3.
Where do we use the volume of a cube in daily life?
We can see many examples of the volume of a cube in daily life.
- A water tank in the shape of a cube can store water equal to the volume of the cube.
- The volume of air occupied in a cube-shaped room.
- The volume of wood required to build a solid cubical block.
- The volume of cube-shaped sweets has to be measured before packing them into sweet boxes to know exactly how much space they will take.
Conclusion
The volume of a cube is a measure of the space occupied by the air inside it. It is used in many areas of everyday life. The room of a building or home can be a cube shaped. The space inside it, where we live and work, is its volume. If you are interested in more simple and concise resources on cubes or other math topics like what is a cube?, what is a unit cube?, and more, you can download the Splashlearn App.
For more math resources for teachers, sign up for free on Splashlearn.com.
Solved Examples
- What is the volume of a cube if its edge is 2 cm?
Solution:
Given that s = 2 cm
Volume of a cube = s × s × s
So, volume of the given cube = 2 × 2 × 2 = 8 cm3
Thus, the total volume of a cube with an edge of 2 cm is 8 cm3.
- The volume of a cubical container is 343 m3. Find the length of side of container.
Solution:
Volume of a cube = s × s × s
343 = s × s × s
$\sqrt[3]{343}$ = s
$\sqrt[3]{7 × 7 × 7}$ = s
So, the length of the side of the container is 7 m.
- Find the volume of a sugar cube with a 5 cm edge.
Solution:
Given that s = 5 cm
Volume of a cube = s × s × s
So, volume of the given cube = 5 x 5 x 5 = 125 cm3. Thus, the total volume of a cube with an edge of 5 cm is 125 cm3.
Practice Problems
Volume Of Cube
What is the volume of the cube whose edge measures 10 cm?
Volume = 10 × 10 × 10 = 1000 cm$^{3}$
How many cubes of 3 cm edge can be put in a cubical box of 9 cm edge?
Number of cubes $ = \frac{9 \times 9 \times 9}{3 \times 3 \times 3} = 27$
Three cubes of metal whose edges are 2 cm, 3 cm and 4 cm respectively, are melted to form a single cube. What is the volume of the new cube?
Volume of new cube = 2$^{3}$ + 3$^{3}$ + 4$^{3}$ = 8 + 27 + 64 = 99 cm$^{3}$
A rubik’s cube has an edge of 0.05 m. What is the volume of the rubik's cube?
0.05 m = 5 cm
Volume of cube = 5 × 5 × 5 = 125 cm$^{3}$
Frequently Asked Questions
Can I calculate the volume of a cube if the diagonal length is given?
Yes, you can calculate the volume using the formula given below: Volume of Cube = $\sqrt{3} \times \frac{d^{3}}{9}$
Is the volume of a cube related to the volume of a cone?
No, the volume of a cone is not related to the volume of a cube. Instead, it is related to the volume of a cuboid. Volume of a cuboid = length × width × height. In a cube, length = width = height. So the volume of cube = side × side × side = side3.
Can we find the volume of a square?
No. A square is a two-dimensional shape. It does not have volume. Conversely, a cube is a three-dimensional shape and has volume. We can say that a cube is the 3D version of a square.
Is the surface area of cube the same as the volume of the cube?
No, the surface area of a cube is not the same as the volume of the cube. The surface area of cube is the sum total of all the planes that form the surface of the cube whereas the volume is the space enclosed within the cube. The formula for the surface area of a cube is 6× s2 while the formula for the volume of cube is s3 where ‘s’ refers to the side of the cube.



























