What is a Cube?
A cube is a solid shape with six square faces. Each square face has the same side length and thus all the faces have the same size.
A cube has 12 edges and 8 vertices. Each vertex refers to a corner where three edges of a cube meet.
We can observe several examples of the cube shape in our everyday life. Cube shaped objects include sugar cubes, rolling dice, ice cubes, and the world-famous Rubik’s Cube!


Let’s explore the properties and the role of the cube in mathematics and in real life.
Recommended Games
Properties of a Cube Shape
- It is a three-dimensional, square-shaped figure
- It has 6 faces, 12 edges, and 8 vertices
- All faces are in the shape of a square
- All sides have the same length
- Each vertex meets three faces and three edges
- The edges run parallel to those parallel to it
- All angles of a cube are right angles
Recommended Worksheets
Surface Area of a Cube
The total surface area of a cube is defined as the area of its outer surface.
Since the cube has six square faces and each of the square faces is of the same size, the total surface area of a cube = 6 ✕ area of one face.
Let’s say the length of each edge is “a”.
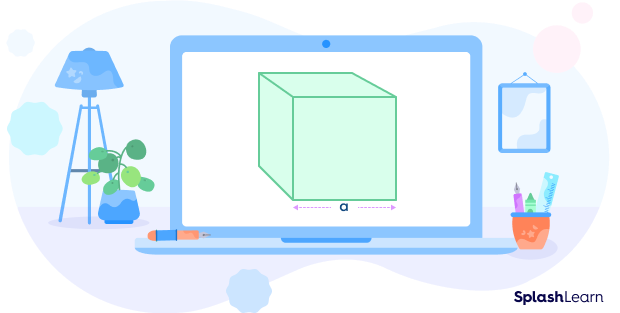
Area of one square face = edge ✕ edge = a ✕ a = a²
Therefore, the total surface area of the cube = 6a²
The total surface area of the cube will be equal to the sum of all six faces of the cube.
The Lateral Surface Area of a Cube
Imagine yourself sitting in a cube shaped room. You can then see the four walls around you. This denotes the lateral surface area of that room. That is, the lateral surface area of a cube shaped room is the area of its four walls, excluding the ceiling and the floor.
The lateral surface area of the cube is the sum of areas of its square faces, excluding the area of the top and the bottom face.
So the lateral surface area of a cube = sum of areas of 4 faces = 4a²
The Volume of a Cube
The volume of a three-dimensional object can be defined as its capacity or the amount of liquid it could hold if it was hollow from the inside.
The volume is calculated by multiplying the object’s length, breadth, and height. In the case of a cube shape, the length, width, and height are all of the same length. Let us refer to it as “a”.
Hence the volume of the cube is a ✕ a ✕ a = a³
Solved Examples
Example 1: The value of each side of a cube is 20 cm. What is the surface area of the cube?
Solution: Let’s use the formula to calculate the surface area where the value of each side is a.
Surface area of the cube = 6a² = 6 ✕ 400 = 2400 cm²
Example 2: The value of each side of a cube is 10 cm. What is the volume of the cube?
Solution: Let’s use the formula to calculate the volume of the cube, where each side is a.
Volume of the cube = a³ = 10 × 10 × 10 = 1000 cm³
Example 3: A cube shaped container with a side of 2 m is to be painted. What is the total surface area to be painted?
Solution: Since each side is 2 m, we will use the formula, 6 ✕ (Side)²Hence, the total surface area to be painted = 6 ✕ 4 = 24 m²
Practice Problems
Cube - Definition With Examples
What is the volume of a cube shaped glass aquarium with a length of 6 inches?
Length of each edge of the cube aquarium = 6 inches.
Formula for the volume of cube = a³, where a is the length of each edge of the cube.
Therefore volume of given cube = 6 ✕ 6 ✕ 6 = 216 inch³
What is the total surface area of a cube if the length of its edge is 30 cm?
Length of each edge of the cube aquarium = 30 cm
Formula for surface area of one square face = edge ✕ edge = axa = 900
Therefore, total surface area of the cube = 6a² = 5400 cm²
What is the lateral surface area of a cube where the length of a side is 6 inches?
The lateral surface area of the cube is the sum of areas of its square faces excluding the area of the top and the bottom face.
So the lateral surface area of a cube = sum of areas of 4 faces = 4a²
Surface area of one square face = a² = 36
Lateral surface area is the sum of areas of 4 faces = 4a² = 144 cm²
Frequently Asked Questions
What is the difference between a cube and a square?
The key difference is that a square is a two-dimensional object, whereas a cube is a three-dimensional object. Hence, a cube has an extra dimension, which is its height.
What are the properties of a cube?
Here are some of the properties of a cube:
1. A cube has six faces in the shape of squares with equal dimensions.
2. Each face diagonal forms two right angles.
3. Every vertex meets three faces and three edges.
How to calculate the volume of a cube?
All sides of a cube are of equal length. Hence, the volume of a cube is a product of its length, breadth, and height, which are all equal in dimension.
Hence, the volume of a cube is e³ cubic units, where “e” is the length of each side.





















