What is a Prism?
A prism is a solid shape that is bound on all its sides by plane faces. There are two types of faces in a prism. The top and bottom faces are identical and are called bases. A prism is named after the shape of these bases. For example, if a prism has a triangular base it is called a triangular prism.
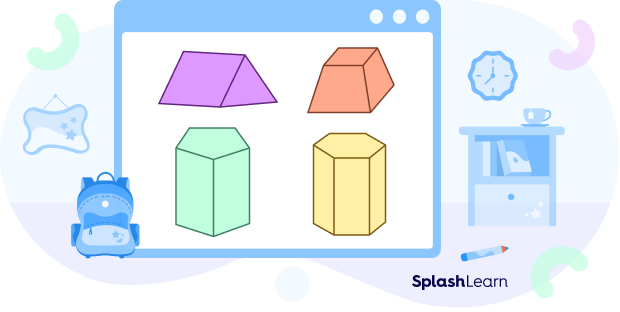
The faces other than the top and bottom of a prism are called its lateral faces. All the lateral faces are also identical to each other and belong to the class of parallelograms. This means that the lateral faces can either be parallelograms, rectangles, or even squares since all of them have their opposite sides parallel to each other. One of the most common examples of a prism is a cuboid. It has a rectangular base and is called a rectangular prism.
Elements of a Prism
A prism can be labeled with its features, which helps characterize them.
Edge: A straight line that connects any two adjacent vertices of a prism is called its edge.
Vertex: The corners of a prism where any two edges meet are called vertices.
Face: It is a closed, flat surface surrounded by vertices and edges.
Cross Sections of a Prism
The cross section of a prism is the shape obtained when a plane intersects a prism along its axis. Based on the shape of the base, prisms can be categorized into the following:
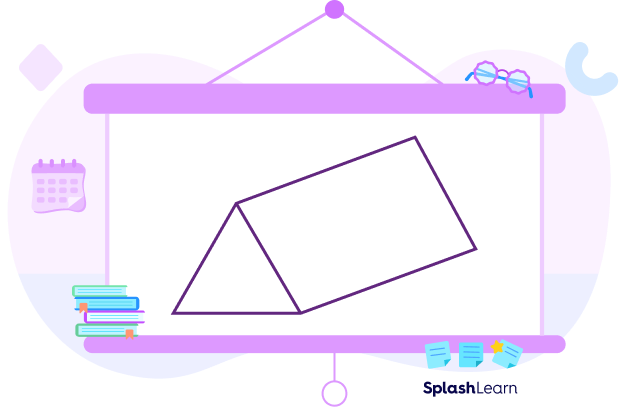
- Triangular prism: The base of the prism is triangular in shape.
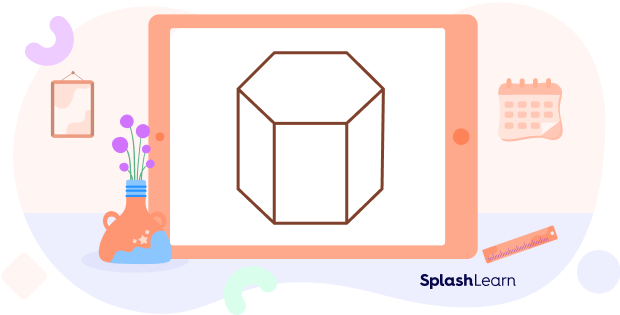
- Hexagonal prism: It is a prism with a base in the shape of a hexagon.
- Square prism: A prism that has a base in the shape of a square. You may have seen a square prism with a different name, it is also called a cube.

- Pentagonal prism: The base of the prism is shaped like a pentagon.

- Rectangular prism: A prism that has bases in the shape of a rectangle. A rectangular prism is also known as a cuboid.

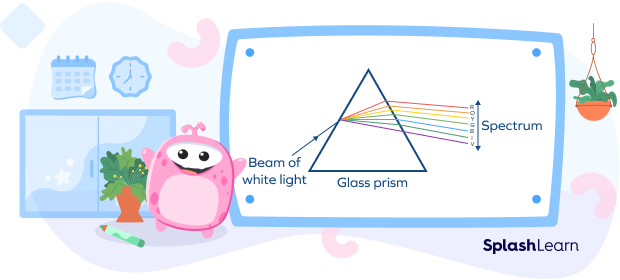
Did you know that an ordinary triangular prism can separate white light into several constituent colors that constitute the spectrum?
Regular and Irregular Prisms
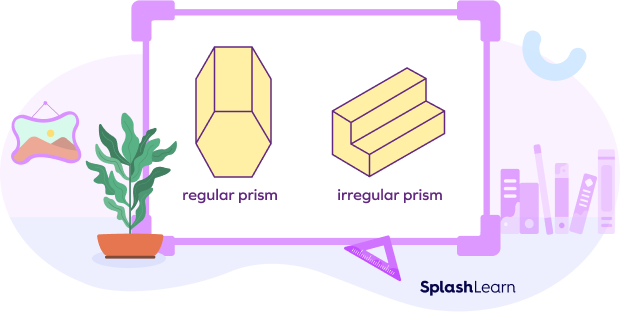
The shape of the base of a prism is used to segregate them into regular and irregular polygons. A regular prism is a base with a regular polygon, whereas a prism whose base is an irregular polygon is called an irregular prism.
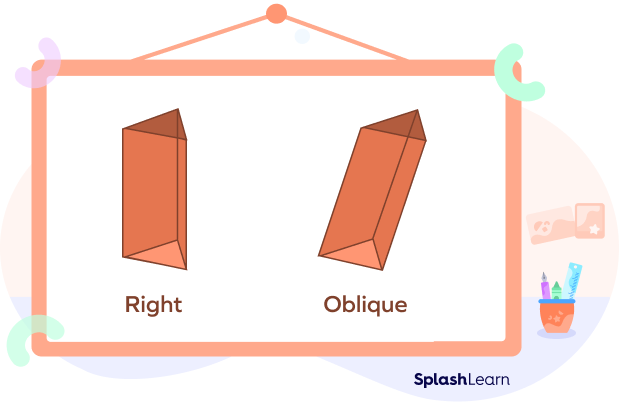
Right Prism and Oblique Prism
A right prism will have two flat ends and they are perfectly aligned with every side face. An oblique prism, on the other hand, will appear to be somewhat tilted with two bases that are not aligned. The side faces of such a prism are parallelograms.
Surface Area of a Prism
For any prism, the surface area of the same can be calculated using the following formula:
Surface Area = (2 ✕ Base Area) + (Base perimeter ✕ Height)
The surface area of a prism is the total area on all of its bases and faces.
Volume of a Prism
The available space within a prism depicts the volume of a prism. To arrive at the volume of a prism, we will need to estimate the area of the cross-sections and then multiply them with the depth of the prism. The volume of a prism can be denoted in cubic units.
The formula to calculate the volume of a prism is as follows:
Volume = Area of base ✕ Height
Solved Examples On Prism
Example 1. Calculate the volume of a prism with a height of 7 cm and an area of the base of 60 cm².
Solution: We know that Volume of prism = Area of base ✕ Height
For the given prism,
Height = 7 cm and Area of base = 60 cm²
Therefore, the volume of the given prism:
Volume = 60 ✕ 7 = 420 cm³
Example 2. Calculate the surface area of a prism with a base area of 25 cm², a base perimeter of 24 cm, and a height of 10 cm.
Solution: We know that for a prism,
Surface Area = (2 ✕ Base Area) + (Base perimeter ✕ Height)
For the given prism,
Height = 10 cm and Area of base = 25 cm² and Perimeter of base = 24 cm,
Therefore, the surface area of the given prism:
Surface Area = (2 ✕ 25) + (24 ✕ 10) = 50 + 240 = 290 cm²
Example 3. Find out the volume of a prism with a base area of 25 cm² and length of 12 cm.
Solution: We know that Volume of prism = Area of base ✕ Height
For the given prism,
Height = 12 cm and Area of base = 25 cm²
Therefore, the volume of the given prism:
Volume = 25 ✕ 12 = 300 cm³
Practice Problems On Prism
What is Prism? Meaning, Definition, Shape, Types, Area
For a pentagonal prism with a length of 12.5 cm, what will be the prism’s volume if the base area is 30 cm².
We know that Volume of prism = Area of base ✕ Height
For the given prism,
Height = 12.5 cm and Area of base = 30 cm²
Therefore, Volume of the given prism:
Volume = 30 ✕ 12.5 = 375 cm³
Which of the following is an example of a prism shape?
A cube is a prism that has square bases and square faces.
If the volume of a rectangular prism is 40 cm³ and the base area is 10 cm², calculate the height of the prism.
We know that Volume of prism = Area of base ✕ Height
For the given prism,
Volume = 12 cm and area of base = 25 cm²
Therefore,
40 = 10 ✕ height
Height = $\frac{40}{10}$ = 4 cm.
Frequently Asked Questions On Prism
How is a prism different from a pyramid?
Although both the prism and pyramid are three-dimensional, a prism has two identical bases whereas a pyramid has only one base.
Can we regard a cylinder as a prism?
Since a prism is a polyhedron with all flat faces, a cylinder is not a prism—it has curved surface.
If the side faces of a prism are rectangles, then what is such a prism called?
In this case, we will call a prism a right prism.
















