Regular Polygon – Definition, Properties, Examples, Facts

What Is a Polygon?

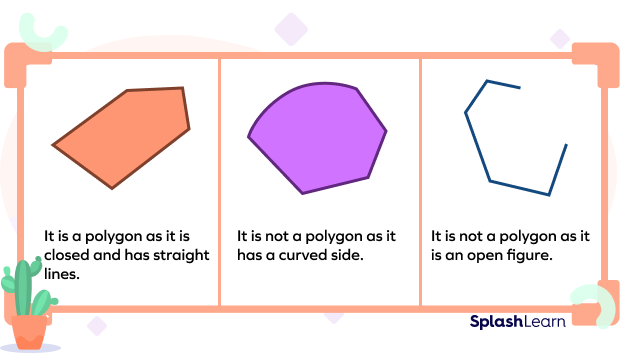
A two-dimensional enclosed figure made by joining three or more straight lines is known as a polygon. They are also known as “flat figures”. Example: A square is a polygon with made by joining 4 straight lines of equal length.

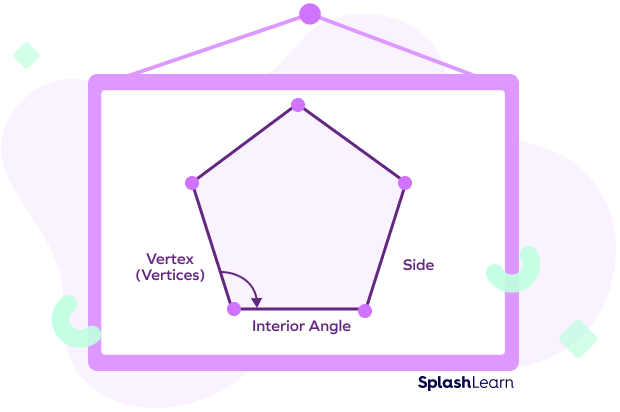
Parts of a Polygon 

A polygon has three parts: 

• Sides: A line segment that joins two vertices is known as a side.
• Vertices: The point at which two sides meet is known as a vertex.
• Angles: interior and exterior. An interior angle is the angle formed within the enclosed surface of the polygon by joining the sides.  

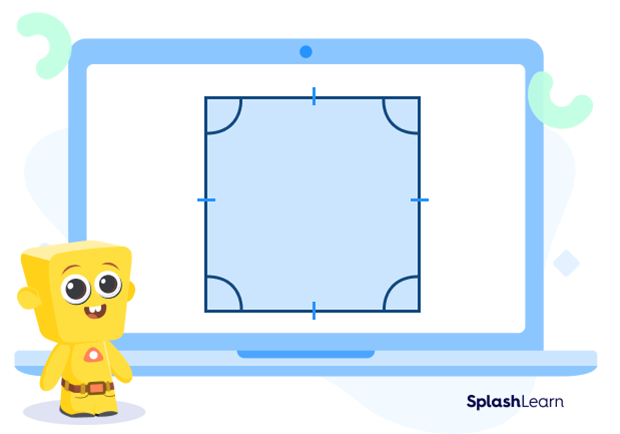
What Are Regular Polygons?

If all the polygon sides and interior angles are equal, then they are known as regular polygons. The examples of regular polygons are square, equilateral triangle, etc. In regular polygons, not only are the sides congruent but so are the angles. That means they are equiangular. 

Properties of Regular Polygons

The properties of regular polygons are listed below: 

• All its sides are equal. 
• All its interior angles are equal. 
• The sum of its exterior angles is 360°. 

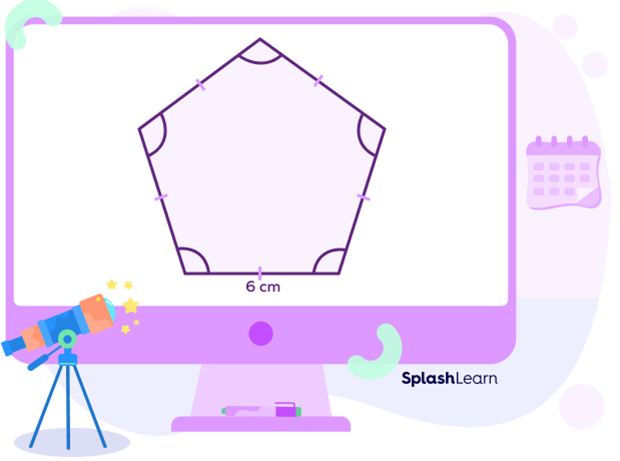
Perimeter of a Regular Polygon

A regular polygon has all the sides equal. And the perimeter of a polygon is the sum of all the sides. So, a regular polygon with n sides has the perimeter = n times of a side measure.

For example, if the side of a regular polygon is 6 cm and the number of sides are 5, perimeter = 5 ✕ 6 = 30 cm

Sum of Interior Angles of a Regular Polygon

Let there be a n sided regular polygon. Since, the sides of a regular polygon are equal, the sum of interior angles of a regular polygon = (n − 2) × 180°

For example, the sides of a regular polygon are 6. 

So, the sum of interior angles of a 6 sided polygon = (n − 2) × 180° = (6 − 2) × 180° 

= 720°

Measure of Each Interior Angle of a Regular Polygon

Since a regular polygon is equiangular, the angles of n sided polygon will be of equal measure. A n sided polygon has each interior angle

= $\frac{Sum of interior angles}{n}$$=$$\frac{(n-2)\times180^\circ}{n}$ 

For example, let’s take a regular polygon that has 8 sides. 

So, each interior angle = $\frac{(8-2)\times180^\circ}{8} = 135^\circ$

Measure of Each Exterior Angle of a Regular Polygon

There are n equal angles in a regular polygon and the sum of an exterior angles of a polygon is $360^\circ$. So, the measure of each exterior angle of a regular polygon = $\frac{360^\circ}{n}$.

Number of Diagonals of a Regular Polygon

The number of diagonals in a polygon with n sides = $\frac{n(n-3)}{2}$ as each vertex connects to (n – 3) vertices. And in order to avoid double counting, we divide it by two. 

For example, if the number of sides of a regular regular are 4, then the number of diagonals = $\frac{4\times1}{2}=2$.

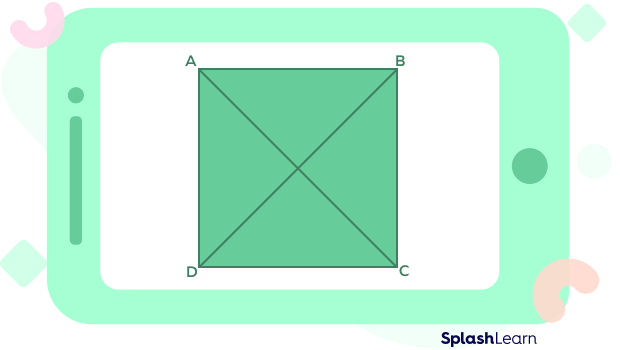
Number of Triangles of a Regular Polygon

If the sides of a regular polygon are n, then the number of triangles formed by joining the diagonals from one corner of a polygon = n – 2

For example, if the number of sides are 4, then the number of triangles formed will be 

(4 – 2) = 2.

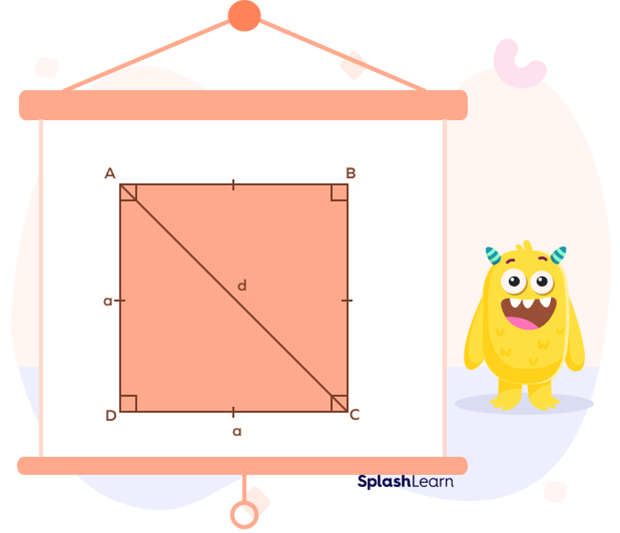
Lines of Symmetry of a Regular Polygon

The line of symmetry can be defined as the axis or imaginary line that passes through the center of the shape or object and divides it into identical halves. Since all the sides of a regular polygon are equal, the number of lines of symmetry = number of sides = $n$

For example, a square has 4 sides. So, the number of lines of symmetry = 4

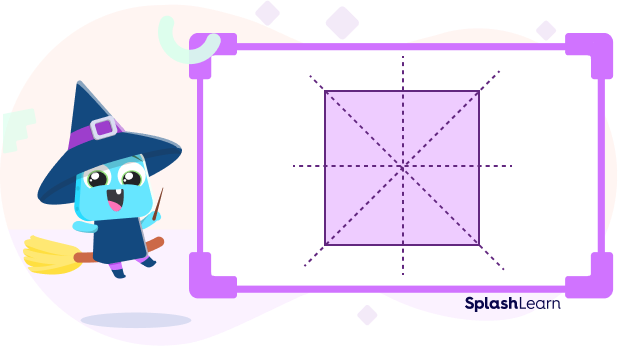
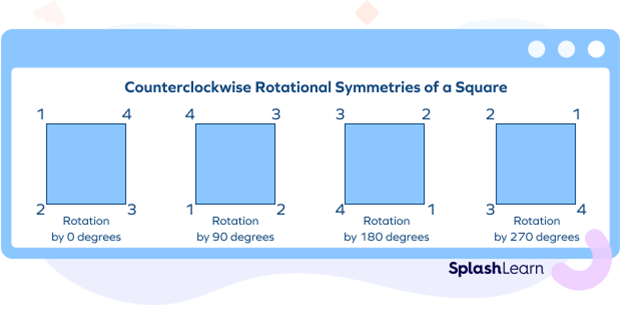
Order of Symmetry of a Regular Polygon

A shape has rotational symmetry when it can be rotated and still it looks the same. The order of a rotational symmetry of a regular polygon = number of sides =  $n$ . Also, the angle of rotational symmetry of a regular polygon =  $\frac{360^\circ}{n}$.

For example, a square has 4 sides. So, the order of rotational symmetry = 4. 

Angle of rotation =$\frac{360}{4}=90^\circ$.

This means when we rotate the square 4 times at an angle of $90^\circ$, we will get the same image each time.

Different Regular Polygons 

The following is a list of regular polygons: 

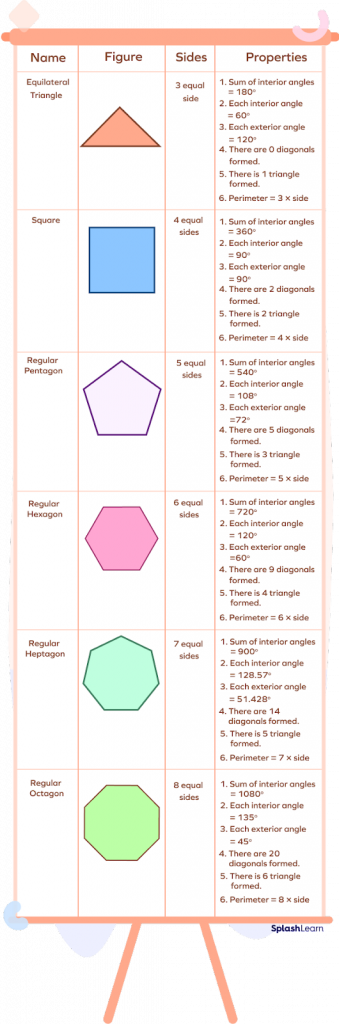
Fun Fact!

Solved Examples on Regular Polygon

Example 1: Find the number of diagonals of a regular polygon of 12 sides.

Solution: The number of diagonals of a n sided polygon = $n\frac{(n-3)}{2}$$=$$12\frac{(12-3)}{2}=54$

Example 2: If each interior angle of a regular polygon is $120^\circ$, what will be the number of sides?

Solution: We know that each interior angle = $\frac{(n-2)\times180^\circ}{n}$, where n is the number of sides.

So, $120^\circ$$=$$\frac{(n-2)\times180^\circ}{n}$

$120n=(n-2)$$\times$$180$

$120n=180n-360$

$n=6$

The number of sides = 6

Example 3: Can a regular polygon have an internal angle of $100^\circ$ each? 

Solution: Each exterior angle = $180^\circ – 100^\circ = 80^\circ$

Each exterior angles = $\frac{360^\circ}{n}$, where n is the number of sides. $80^\circ$ = $\frac{360^\circ}{n}$$\Rightarrow$ $n$ = 4.5, which is not possible as the number of sides can not be in decimal.

Practice Problems on Regular Polygon

Frequently Asked Questions on Regular Polygon