Rhombus – Definition, Properties, Area, Perimeter, Examples

What is Rhombus?

Rhombus is a quadrilateral with all equal sides. Since opposite sides of a parallelogram are equal so, rhombus is a special type of a parallelogram whose all sides are equal.

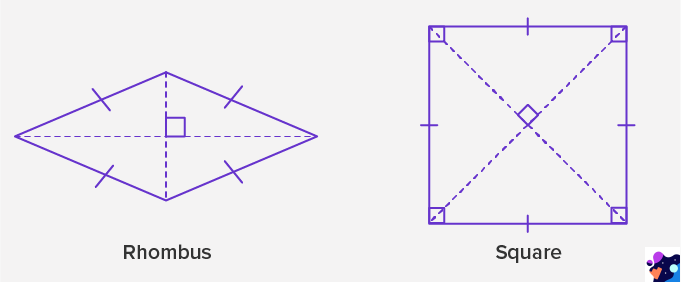
How is a Rhombus Different from a Square?

The difference between a square and a rhombus is that all angles of a square are right angles, but the angles of a rhombus need not be right angles. 

So, a rhombus with right angles becomes a square.

We can say, “Every square is a rhombus but all rhombus are not squares.”

Real-life Examples

Rhombus can be found in a variety of things around us, such as finger rings, rhombus-shaped earring, the structure of a window glass pane, etc.

Properties of a Rhombus

Some of the properties of a rhombus are stated below.

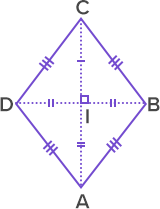
• All sides of a rhombus are equal. Here, AB = BC = CD = DA.
• Diagonals bisect each other at 90°. Here, diagonals AC and BD bisect each other at 90°.
• Opposite sides are parallel in a rhombus. Here, AB ∥ CD and AD ∥ BC.
• Opposite angles are equal in a rhombus. ∠A = ∠C and ∠B = ∠D.
• Adjacent angles add up to 180°.

∠A + ∠B = 180°

  ∠B + ∠C = 180°

  ∠C + ∠D = 180°

  ∠A + ∠D = 180°

• All the interior angles of a rhombus add up to 360°.
• Adjacent angles of a rhombus add up to 180°.
• The diagonals of a rhombus are perpendicular to each other. Here, AC ⟂ BD.
• The diagonals of a rhombus bisect each other. Here, DI = BI and AI = CI.
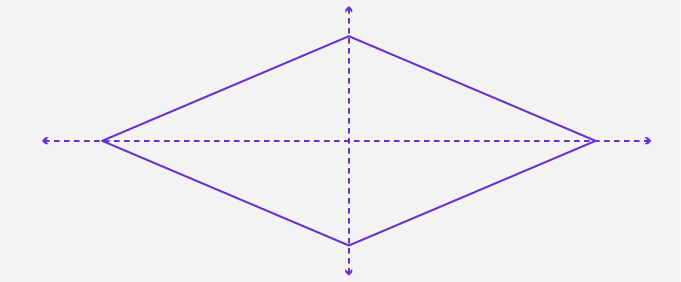
• A rhombus has rotational symmetry of 180 degrees (order 2). That is, a rhombus retains its original orientation when rotated by an angle 180 degrees.
• The diagonals of a rhombus are the only 2 lines of symmetry that a rhombus has. These divide the rhombus into 2 identical halves. 

Area of a Rhombus

The area of a rhombus is the region enclosed by the 4 sides of a rhombus.

There are two ways to find the area of a rhombus.

1. Area of a Rhombus When its Base and Altitude are Known

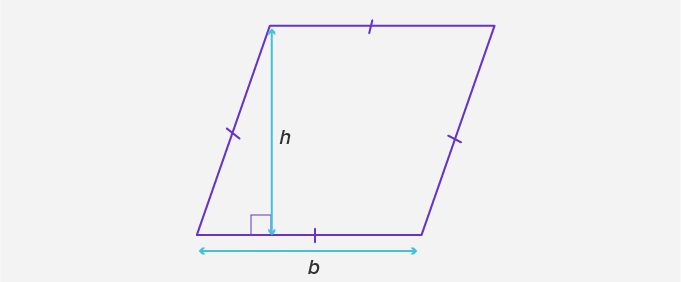
Area of rhombus is calculated by finding the product of its base and corresponding altitude (height).

So, Area of rhombus = base × height = (b × h) square units.

2. Area of a Rhombus When its Diagonals are Known

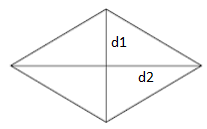
When length of the diagonals of a rhombus are known, then its area is given by half of their product.

So, Area of rhombus = $\frac{(d1\times d2)}{2}$ square units; where d1 and d2 are the diagonals of a rhombus.

Perimeter of Rhombus

The perimeter of a rhombus is the total length of its boundaries. As all the four sides of a rhombus are equal, its perimeter is calculated by multiplying the length of its side by 4.

That is, Perimeter of a rhombus = 4 × a units; where ‘a’ is the length of the side of the rhombus.

Solved Examples on Rhombus

Example 1: The length of two diagonals of rhombus are 18 cm and 12 cm. Find the area of rhombus.

Solution:

Diagonal (d1) = 18 cm

Diagonal (d2) = 12 cm

Area of rhombus = $\frac{(d1\times d2)}{2}$ = $\frac{(18\times 12)}{2}$ sq.cm = 108 sq.cm

Example 2: Find the perimeter of the rhombus with its side measuring 15 cm.

Solution:

Length of side of rhombus (a) = 15 cm

Perimeter of rhombus = 4 × a = 4 × 15 cm = 60 cm

Example 3: The area of a rhombus is 56 sq. cm. If the length of one of its diagonals is 14 cm, find the length of the other diagonal.

Solution:

Area of rhombus = 56 sq.cm

d1 = 14 cm

We know, area of rhombus = $\frac{(d1+d2)}{2}$

 ⇒ 56 = $\frac{(14\times d2)}{2}$

⇒ 56 = 7 × d2

⇒ d2 = 56 ÷ 7 

⇒ d2 = 8 cm

So, the second diagonal of the given rhombus measures 8 cm.

Example 4: In rhombus, ABCD, if ∠A = 60°, find the measure of all other angles.

Solution:

∠A + ∠B = 180° (Adjacent angles adds up to 180°)

60° + ∠B = 180° (Given, ∠A = 60°)

∠B = 180° – 60°

∠B = 120°

∠C = ∠A = 60° (Opposite angles are equal in a rhombus)

∠D = ∠B = 120° (Opposite angles are equal in a rhombus)

Practice Problems on Rhombus

Rhombus Attend this Quiz & Test your knowledge. 1 Which of the following quadrilaterals is definitely a rhombus? Trapezium Rectangle Square Parallelogram CorrectIncorrect Correct answer is: Square All sides of a square are equal, so all squares are rhombus. 2 If the length of one of the sides of the rhombus is 10 cm. What will be the length of the opposite side of the given rhombus? 5 cm 10 cm 20 cm 40 cm CorrectIncorrect Correct answer is: 10 cm All sides of the rhombus are equal in length. 3 What will be the altitude of the rhombus whose area is 320 sq. cm and its side is 40 cm? 4 cm 6 cm 8 cm 10 cm CorrectIncorrect Correct answer is: 8 cm Area = base × altitude ⇒ 320 = 40 × altitude ⇒ altitude = 320 ÷ 40 = 8 cm 4 The area of the floor of a hall equals 500,000 sq. cm. If the floor is to be covered with tiles with each of its diagonal measuring 40 cm and 25 cm, find the number of tiles required. 50 500 1000 5000 CorrectIncorrect Correct answer is: 1000 Area of floor = 500,000 sq. cm Area of each tile = $\frac{(d1\times d2)}{2}$ = $\frac{40\times 25}{2}$ = 500 sq. cm Number of tiles = Area of floor ÷ Area of 1 tile = 500,000 ÷ 500 = 1,000 tiles So, 1,000 tiles are required to cover the floor.

Frequently Asked Questions on Rhombus