Diagonals in Geometry
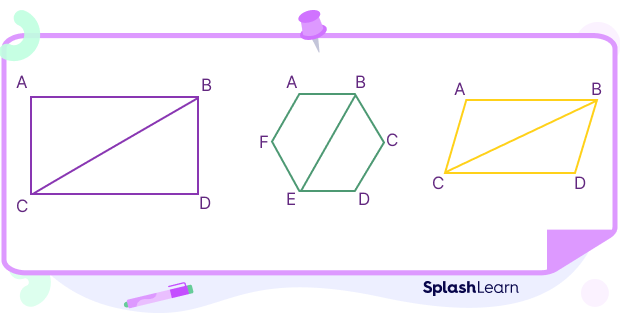
A polygon is defined as a flat or plane, two-dimensional closed shape bounded with straight sides. A diagonal is a line segment connecting the opposite vertices (or corners) of a polygon. In other words, a diagonal is a line segment connecting two non-adjacent vertices of a polygon. It joins the vertices of a polygon, excluding the edges of the figure. The following shapes have a diagonal drawn on them:
History of the Diagonal
The word diagonal comes from the ancient Greek word diagonios, which means “from angle to angle.” Both Euclid and Strabo used it to describe a line that connects two vertices of a cuboid or a rhombus; later, it became known in Latin as diagonus (slanting line).
Diagonals of Polygon
Diagonal Formula
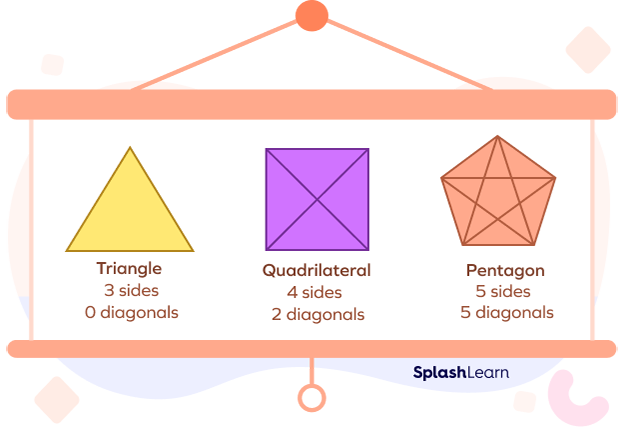
Diagonals for polygons of all shapes and sizes can be made and for every shape; there is a formula to determine the number of diagonals.
The number of diagonals in a polygon with n vertices = $\frac{n(n-3)}{2}$
So, from this formula, we can easily calculate the number of diagonals in a polygon.
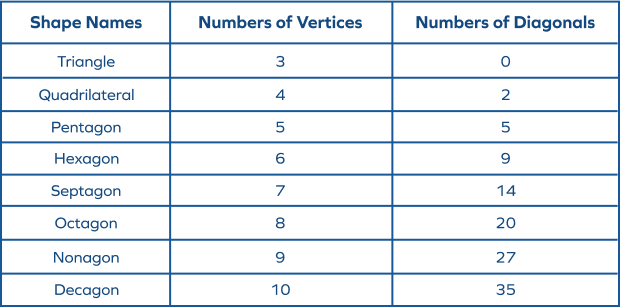
The given table shows the number of diagonals in different polygons:
Diagonals of Solid Shapes
Just like polygons, solid or 3D shapes also have diagonals. Based on the number of edges, the number and properties of diagonals vary for different solids. The following solids have some diagonals drawn on them:
Length of a Diagonal
The length of diagonals of any shape depends on the dimensions of its sides.
Length of Diagonal of Square
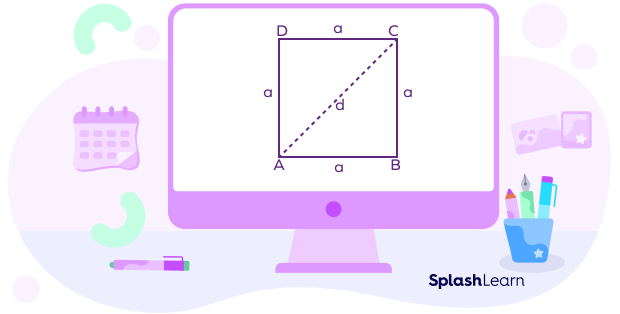
The length of the diagonal of a square can be derived using the Pythagoras theorem. A diagonal of a square divides it into two right-angled triangles. Applying the Pythagoras theorem, we can find the length of the diagonal (d) of a square with side (a) as a$\sqrt{2}$.
Diagonal length of a square with each side a units = a$\sqrt{2}$ units
Length of Diagonal of Rectangle
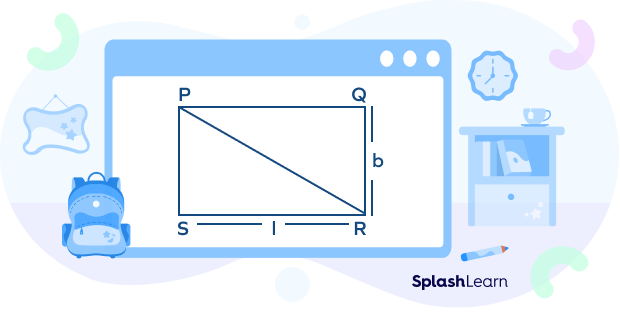
A diagonal of a rectangle divides it into two right-angled triangles. Applying the Pythagoras theorem, we can find the length of diagonal of a rectangle with length (l) and breadth (b) as
d$^{2}$ = l$^{2}$ + b$^{2}$
So, d = $\sqrt{l^{2} + b^{2}}$, where d is diagonal, l is length, and b is the breadth of the rectangle.
Solved Examples on Diagonals
- What is the total number of diagonals in a polygon of 12 sides?
Solution:
The number of diagonals in a polygon with n vertices = $\frac{n(n-3)}{2}$
Therefore, the number of diagonals in a polygon with 12 sides = $\frac{12(12-3)}{2}$ = 54
- What is the length of the diagonal of a square with each side 6 cm long?
Solution:
Side, a = 6 cm
Length of the diagonal = a $\times \sqrt{2}$
= 6 $\times \sqrt{2}$
= 6$\sqrt{2}$ cm
- Rahul is strolling across a rectangular park that is 20 meters long and 15 meters wide. Determine the diagonal of the rectangular park.
Solution:
Length of the rectangular park = 20 m, Breadth of the rectangular park = 15 m
Length of the diagonal = $\sqrt{l^{2} + b^{2}}$
= $\sqrt{20^{2} + 15^{2}}$
= $\sqrt{400 + 225}$
= $\sqrt{625}$
= 25 m
Practice Problems on Diagonals
Diagonal
What is the total number of diagonals in a hexagon?
Number of diagonals in hexagon (6 vertices) = $\frac{6(6-3)}{2}$ = 9
The length of the rectangle is thrice its breadth. Which of the following is the diagonal length if the rectangle's breadth is 2 cm?
Breadth and Length of the rectangle is 2 cm and 6 cm respectively.
Length of the Diagonal = $\sqrt{2^{2} + 6^{2}}$ = $\sqrt{4+36}$ = $\sqrt{40}$ = $2\sqrt{10}$ cm
Which of the following is the perimeter of the square whose diagonal is 6$\sqrt{2}$ cm long?
Diagonal of a square with side length a is a$\sqrt{2}$ . Since a$\sqrt{2}$ = 6$\sqrt{2}$, a must be 6 cm.
Therefore, the perimeter of the square must be 4 × 6 cm or 24 cm.
Frequently Asked Questions on Diagonals
Which polygon has an equal number of sides and diagonals?
A pentagon has five sides and five diagonals. <br>
Number of diagonals in a polygon with n vertices = $\frac{n(n-3)}{2}$ <br>
Number of diagonals in a pentagon = $\frac{5(5-3)}{2}$ = 5
Why does the triangle not have any diagonal?
A polygon’s diagonal is a line connecting a vertex to a non-adjacent vertex. As a result, the simplest polygon, a triangle, seems to have no diagonals. We can’t connect a line from one internal angle to another that isn’t also a side of the triangle.
Which quadrilaterals have diagonals that bisect each other?
When each diagonal of a polygon cuts the other diagonal into two equal parts, they are said to bisect each other. The quadrilaterals with bisecting diagonals are rectangle, square, parallelogram, and rhombus.
















