What Is Parallelogram?
A parallelogram is a special type of quadrilateral that has both pairs of opposite sides parallel and equal.
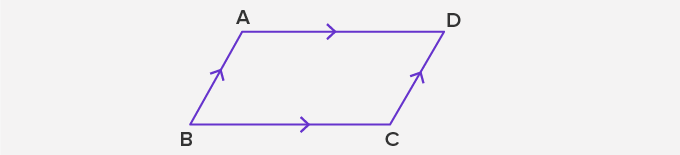
The given figure shows a parallelogram ABCD, which has AB II CD and AD II BC. Also, AD = BC and AB = CD.
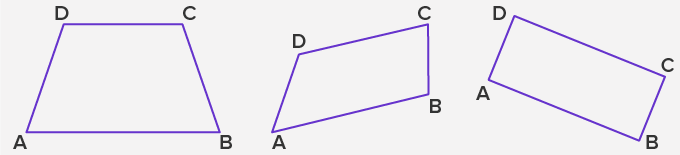
Non-Example:
A trapezium is a non-example of a parallelogram.
Recommended Games
Real-Life Examples of a Parallelogram
When we look around us, we can see multiple parallelogram-like shapes and objects in the form of buildings, tiles, or paper.
Buildings: Many buildings are constructed, keeping in mind the shape of parallelograms. A famous real-life illustration is the Dockland Office Building in Hamburg, Germany.
Tiles: Tiles come in various shapes and sizes. One of the most found tile shapes is a parallelogram.
Eraser: Everyone is familiar with the classic eraser. Erasers, too, come in several shapes and sizes, one of them being that of a parallelogram. The faces of this eraser are in the shape of a parallelogram.

Properties of Parallelograms
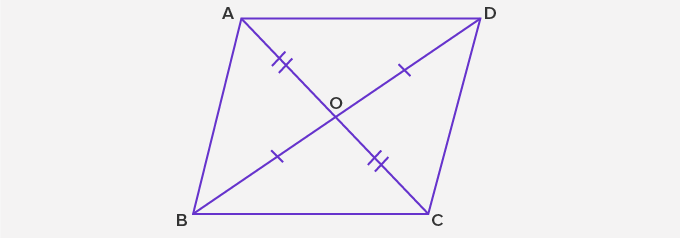
- In a parallelogram, the opposite sides are parallel to each other. Here, AB || CD and AC || BD.
- The opposite sides of a parallelogram are equal in length. Here, AB = CD and AC = BD
- The measurement of opposite angles of a parallelogram is equal. Here, ∠A = ∠C and ∠B = ∠D
- Like all other quadrilaterals, the sum of all the angles of a parallelogram is 360°.
- The adjacent or the adjoining angles of a parallelogram add up to 180°. Therefore, ∠A + ∠B = 180°, ∠B + ∠C = 180°, ∠C + ∠D = 180°, and ∠D + ∠A = 180°.
- The diagonals of a parallelogram bisect each other. Here, OB = OD, and OA = OC.
- The diagonals AC and BD in the figure divide the parallelogram into two congruent triangles.
Types of Parallelograms
There are three unique kinds of parallelograms:
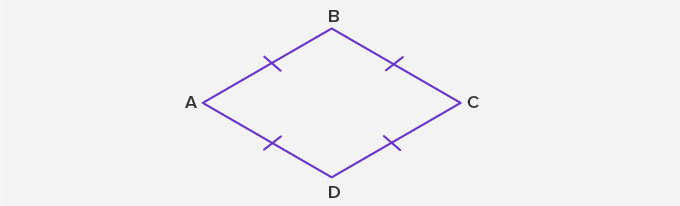
- Rhombus: A rhombus is a parallelogram in which all sides are equal. Here, AB = BC = CD = DA. ABCD is a rhombus.
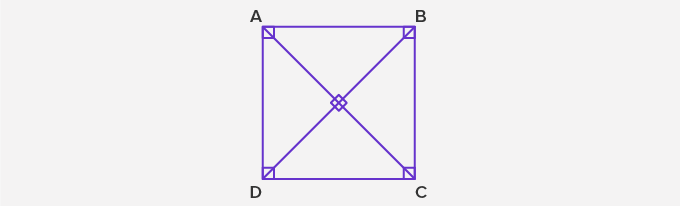
- Square: A square is a parallelogram where all sides and diagonals are equal. The angles are right angles. Here, AB = BC = CD = DA and ∠A = ∠B =∠C =
∠D = 90 degrees and also AD = BC. ABCD is a square.
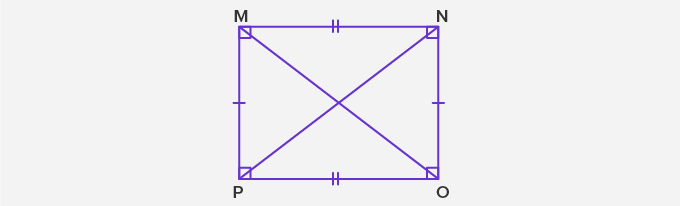
- Rectangle: A rectangle is a parallelogram in which all angles are 90°, and the diagonals are equal. The opposite sides have equal lengths. Here all angles are right angles. Diagonals PN and OM are equal. MNOP is a rectangle.
Area of a Parallelogram
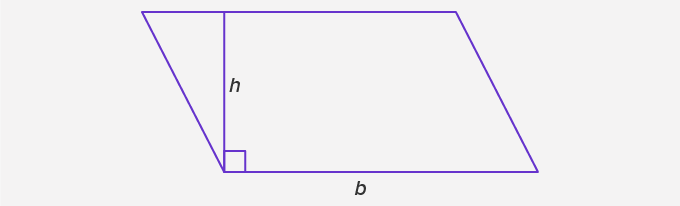
The area of a parallelogram is given by the formula A = bh, where b is the length of the base, and “h” is the height.
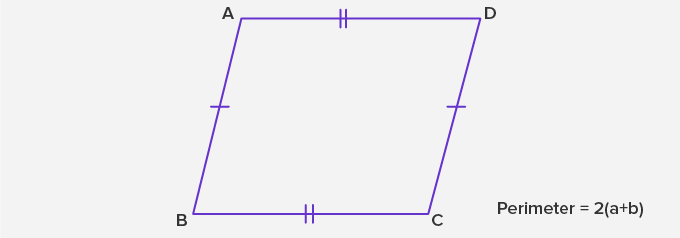
The Perimeter of a Parallelogram
The perimeter of a parallelogram equals the sum of the lengths of the four sides. Since the opposite sides of a parallelogram are equal, its perimeter can also be expressed as 2 x the sum of adjacent sides, i.e., 2 (AB + BC)
SplashLearn is transforming education for elementary school kids from Kindergarten to Grade 5. SplashLearn motivates kids to study math through highly engaging and personalized programs. Available across all digital platforms, it has been used by over 40 million kids worldwide.
Solved Examples On Parallelogram
Example 1
In the figure below, ABCD is a parallelogram where ∠DAB = 75° and ∠CBD = 60°. Calculate ∠BDC.
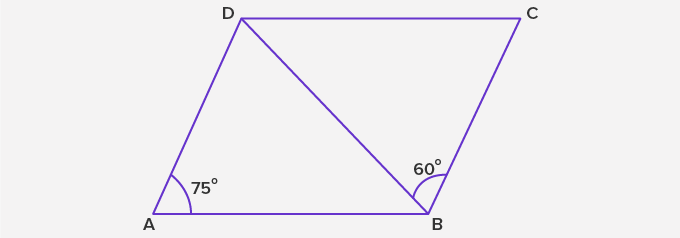
Solution:
As we know, the opposite angles of a parallelogram are equal. Therefore, ∠DCB = ∠DAB = 75°.
We also know that the sum of the angles of a triangle is 180°. Now, consider
∆ BCD. Here, ∠BDC + ∠DCB + ∠CBD = 180°
We know that ∠DCB = ∠DAB = 75°. Therefore,
∠BDC + ∠DCB + ∠CBD = 180°
⇒ ∠BDC + 75° + 60° = 180°
⇒ ∠BDC + 135° = 180°
⇒ ∠BDC = 180° – 135° = 45°
Therefore, ∠BDC = 45°
Example 2
Find the area of this parallelogram with a base of 15 centimeters and a height of 6 centimeters.
Solution:
A = b × h
A = (15 cm) × (6 cm)
A = 90 cm2
Example 3
Two adjacent sides of a parallelogram are 5 cm and 3 cm. Find its perimeter.
Solution:
We know that opposite sides of a parallelogram are equal.
Suppose we have a parallelogram ABCD, then:
AB = CD = 5 cm and
BC = AD = 3 cm
Perimeter of parallelogram = 2 (AB + BC) = 2 (5 + 3) cm
= 16 cm
Practice Problems On Parallelogram
Parallelogram
What is the perimeter of a parallelogram ABCD where the two adjacent sides are 12m and 8m, respectively?
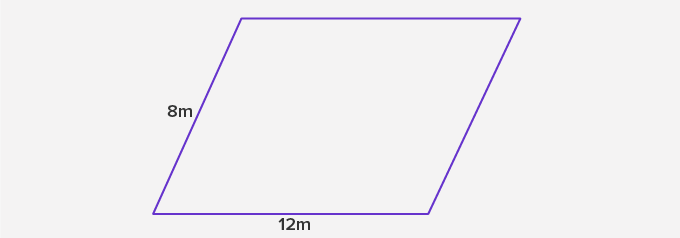
Permieter of a parallelogram = 2 x sum of adjacent sides = 2 (12m + 8m) = 40m
Which of the following is not a parallelogram?
A parallelogram has both the pair of opposite sides as parallel and equal, whereas a trapezium has only one pair of parallel sides and no equal sides.
In a parallelogram ABCD, if ∠A = 60°, then ∠D is equal to
Opposite angles of a parallelogram are equal. So ∠A = ∠C = 60° and also ∠B = ∠D
Also, ∠A + ∠B + ∠C + ∠D = 360°
60° + ∠B + 60° + ∠D = 360°
120° + ∠B + ∠D = 360°
∠B + ∠D = 240° and ∠B = ∠D
Therefore, ∠D = 120°
Frequently Asked Questions On Parallelogram
Is a trapezium a parallelogram?
No, a trapezium is not a parallelogram because there are two pairs of parallel sides in a parallelogram, whereas a trapezium has only one pair of parallel sides.
Are all rectangles parallelograms?
Yes, all rectangles are parallelograms because a rectangle has two sets of parallel sides and two pairs of opposite sides that are equal. Therefore, it abides by all the properties of a parallelogram.
Are all parallelograms rectangles?
No, a parallelogram is not always a rectangle. In a rectangle, all angles must be equal to 90°. But for a parallelogram, no angles need to be equal to 90°.
Do diagonals of a parallelogram always bisect each other?
Yes, diagonals of a parallelogram always bisect each other.
Is it necessary that all sides be equal in a quadrilateral to be a parallelogram?
No, a parallelogram does not have all sides equal. Only opposite sides of a parallelogram are equal.

















