What is Rectangle?
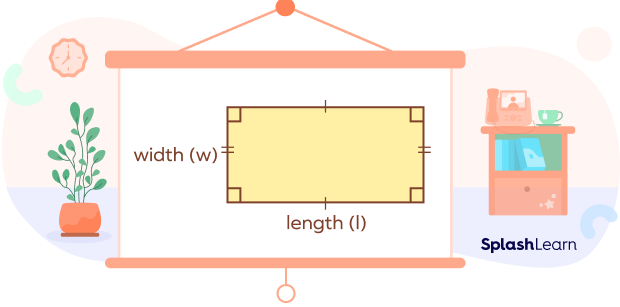
A rectangle is a closed 2-D shape, having 4 sides, 4 corners, and 4 right angles (90°). The opposite sides of a rectangle are equal and parallel. Since, a rectangle is a 2-D shape, it is characterized by two dimensions, length, and width. Length is the longer side of the rectangle and width is the shorter side.
Recommended Games
Rectangles Around Us
Rectangle being the most common shape forms a part of our day to day life. Some real-life examples of the rectangle are given below.

Recommended Worksheets
What Else Can We Call a Rectangle?
- Since, all the angles of a rectangle are equal, we also call it an equiangular quadrilateral. A quadrilateral is a 4-sided closed shape.
- Since, a rectangle has parallel sides, we can also call it a right-angled parallelogram. A parallelogram is a quadrilateral whose opposite sides are equal and parallel. Rectangles are special case of paralleograms.
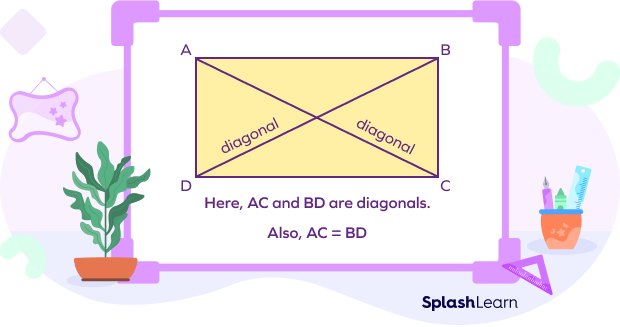
What is a Diagonal of a Rectangle?
The line segments that join the opposite corners of a rectangle are called diagonals. In the given figure, the two diagonals of the rectangle are AC and BD. The diagonals of a rectangle are the same in length. Therefore, AC = BD.
If we know the length and width of a rectangle, we can use Pythagorean Theorem to find the length of its diagonal.
In the given figure, ADB forms a triangle right-angled at A. The diagonal (BD) of the rectangle forms its hypotenuse.
so, using the pythagorean theorem, we get,
diagonal$^{2}$ = length$^{2}$ + width$^{2}$
∴ diagonal = $\sqrt{length^{2} + width^{2}}$
Properties of a Rectangle
The properties of a rectangle are as given below:
- It is a flat and closed shape.
- It has 4 sides, 4 angles, and 4 corners (vertices).
- It has 2 dimensions, namely, length and width
- Every angle of a rectangle measures 90°.
- Opposite sides are equal and parallel.
- It has 2 diagonals of equal length.
Area and Perimeter of a Rectangle
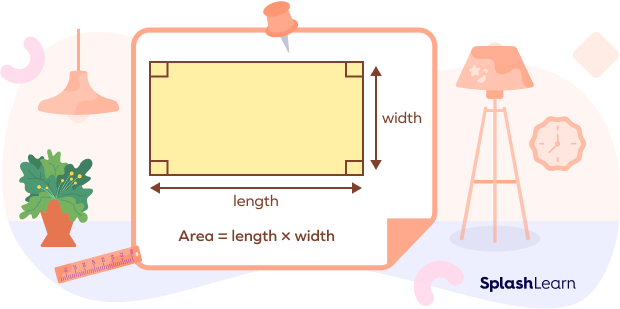
Area of a Rectangle
The space occupied by a rectangle is termed as its area. The area of a rectangle can be calculated by finding the product of its length and width. So,
Area of a rectangle = Length × Width
Since the area of a rectangle is the product of the length and width, it is measured in square units, like, square meters (m2), square inches (in2) and so on.
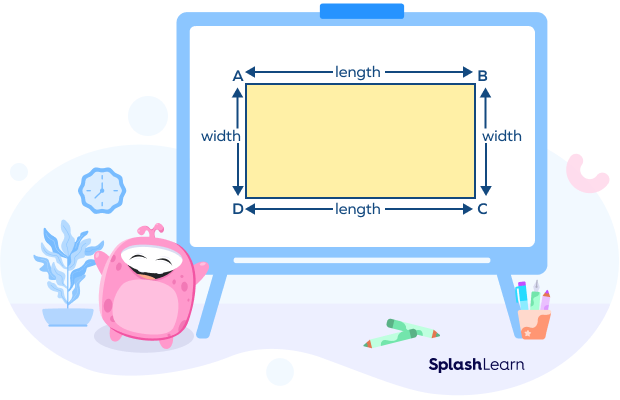
Perimeter of a Rectangle
The perimeter of a rectangle is the sum of the length of its four sides. Let’s find the formula for the perimeter of a rectangle.
Perimeter of a rectangle = length + width + length + width
= 2 × length + 2 × width
= 2 (length + width)
Since, we are adding the units of length to find the perimeter, its unit is also the
The perimeter is measured in the unit of length (inches or feet or metre and so on) because we add the length of the sides to find the answer.
Fun Facts
- All rectangles are parallelograms, but all parallelograms are not rectangles
- The diagonals of a rectangle divide the rectangle into four triangles
- Every square is a rectangle, but every rectangle is not a square
Solved Examples On Rectangle
- Identify rectangles in the given figures.
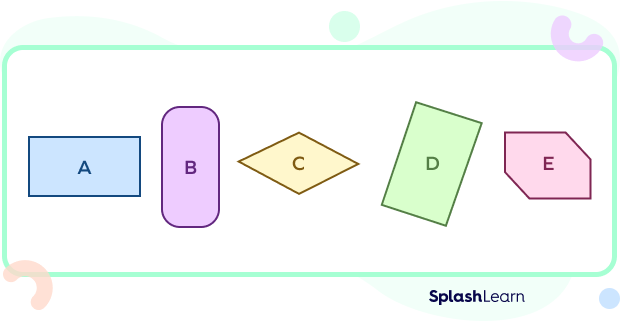
Solution:
Shape A and D are rectangles because they have opposite sides equal and parallel and all four right angles.
- Identify the length, width and diagonal in the given rectangle.
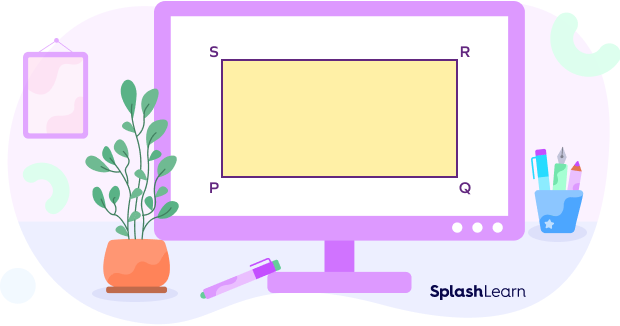
Solution:
Length → PQ and RS
Width → SP and RQ
Diagonals → PR and QS
- The length and width of a rectangle are 7 inches and 21 inches respectively. Find its perimeter.
Solution:
Perimeter of a rectangle = 2 × (Length + Width)
= 2 × (7 + 21) inches
= 2 × (28) inches
= 56 inches
- The length and width of a rectangle are 0.3 m and 15 cm. Find its area.
Solution:
Length = 0.3 m and Width = 15 cm
The length and width of the rectangle are in different so, so we convert one of them. Let’s convert length into centimeters by multiplying it by 100 because 1 m = 100 cm.
So, length = 0.3 ✕ 100 cm = 30 cm
Area = length ✕ width = 30 cm ✕ 15 cm = 450 cm2.
- Find the length of the diagonal of a rectangle whose sides are 8 inches and 5 inches.
Solution:
Length of the diagonal = $\sqrt{length^{2} + width^{2}} = \sqrt{8^{2} + 6^{2}} = \sqrt{64+36} = \sqrt{100} = \sqrt{10 ✕ 10}$ = 10 inches
Practice Problems On Rectangle
Rectangle
What is the area of a rectangular cardboard 1 m long and 30 cm wide?
Length of the cardboard = 1 m = 100 cm and width = 30 cm
Area of rectangular cardboard = 100 cm ✕ 30 cm = 3,000 sq. cm
What is the perimeter of a rectangle with length 16 feet and width 7 feet?
Perimeter = 2 × (16 + 7) cm = 2 × 23 feet = 46 feet
What is the width of the rectangle whose length and area are 8 cm and 32 cm2 respectively?
Area = Length × Width
So, Width = Area ÷ Length of the rectangle = 32 ÷ 8 = 4 cm.
Frequently Asked Questions On Rectangle
What is the definition of a rectangle?
A rectangle is a closed 2-D shape, having 4 sides, 4 corners, and 4 right angles (90°).The opposite sides of a rectangle are equal and parallel.
What are some real-life examples of a rectangle?
Some real-life examples of a rectangle include books, door, table top, blackboard etc.
What is the difference between a rectangle and a parallelogram.
All sides of a square are equal whereas opposite sides of a rectangle are equal and parallel.
Why are all rectangles not squares?
All rectangles are not squares because by definition of a rectangle, its opposite sides must be equal but Its adjacent may or may be be equal. So, only rectangles with equal adjacent sides are squares.
























