Square – Introduction
Take a look at the images given below. You might have come across objects like a photo frame, or a craft paper in day-to-day life. Can you identify what is common in them?
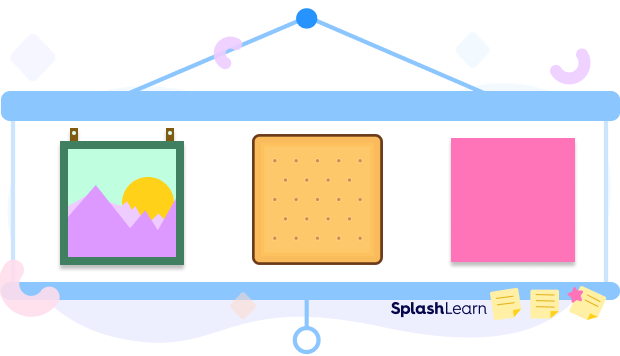
All of them have a square shape.
Recommended Games
Definition of Square in Math
A square is a regular polygon having four equal sides and equal angles that measure 90° each.
Recommended Worksheets
What is a Square in Math?
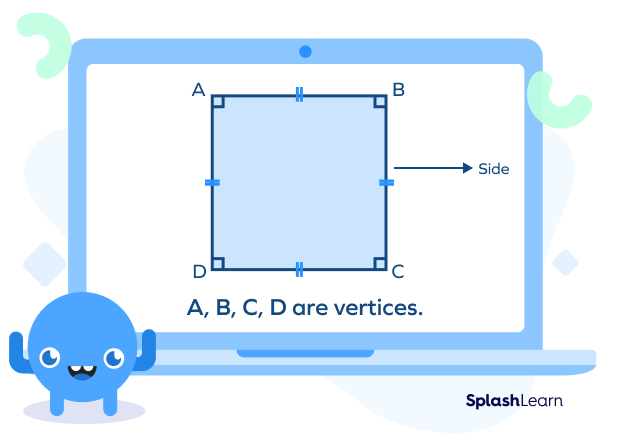
A square is a two-dimensional closed shape with 4 equal sides and 4 vertices. Its opposite sides are parallel to each other. We can also think of a square as a rectangle with equal length and breadth.
Looking around, you can find many things that resemble the square shape. Common examples of this shape include a chessboard, craft papers, bread slice, photo frame, pizza box, a wall clock, etc.

Properties of a Square
- It has 4 sides and 4 vertices.
- Its sides are equal in length.
- All interior angles are equal and right angles, which means that each angle measures 90°.
- The sum of all the interior angles is 360°.
- Its two diagonals bisect each other at right angles.
Area and Perimeter of a Square
Area represents space occupied by a shape or figure whereas perimeter is the length of the outer boundary of the shape. Let’s discuss the formula for finding the area and perimeter of a square.
Area
The area of a two-dimensional shape is defined as the amount of space covered by the shape if we were to keep it on a flat table.
For a square of side length “s” units, the area is given by the formula:
Area $= \text{side} \times \text{side} = \text{S}^2$
The area is expressed in square units, such as $\text{cm}^2$, $\text{cm}^2$, etc.
Perimeter
The perimeter of a two-dimensional shape is defined as the total length of its boundary.
For a square of side length “s” units, the perimeter is given by the formula:
Perimeter $= \text{side} + \text{side} + \text{side} + \text{side} = 4$ $\text{x}$ $\text{s}$
The perimeter is expressed in linear units, such as cm, inches, m, etc.
Solved Examples On Square
Example 1: The side of a square paper is 12 feet. Find the area of the paper.
Solution:
We know that the area of a square is given by $\text{s}^2$, where $\text{s} =$ length of the side.
For the given square, s $= 12$ feet
Therefore, the area of the square paper is given by:
Area $= \text{s}^2 = 12 \times 12 = 144$ sq. ft.
Example 2: If the perimeter of a square measures 68 cm, what is the measure of its side?
Solution:
We know that the perimeter of a square is given by 4 x side.
It is given that the perimeter is 68 cm.
Therefore, 4 x side $= 68$
Which means, side $= \frac{68}{4} = 17$ cm
Example 3: What is the perimeter of a square that has a side of 15 meters?
Solution: We know that the perimeter of a square is given by 4 x s, where s represents the length of each side.
It is given that the side s $= 15$ meters.
Therefore, perimeter $= 4 \times 15 = 60$ meters.
Practice Problems On Square
Square
If the side of a square chess board is 20 cm in length, find the board's perimeter.
We know that the perimeter of a square is given by 4 x s,
where s represents the length of each side.
It is given that the side s $= 20$ cm.
Therefore, the perimeter $= 4 x 20 = 80$ cm.
What is the measure of an interior angle of a square?
Since all the interior angles of a square are right angles, the measure of each one of them is 90 degrees.
What is the area of a square with a side length of 25 cm?
We know that the area of a square is given by $\text{s}^2$, where $\text{s} =$ length of the side.
It is given that the side $\text{s} = 25$ cm.
Therefore,
Area $= \text{s}^2 = 25 \times 25 = 625$ sq. cm.
Frequently Asked Questions On Square
How to identify a polygon as a square?
A polygon that is made of four equal sides, with all the interior angles measuring 90 degrees, is a square.
Is the side of a square and its diagonal the same length?
No, the side of a square and its diagonal aren’t of the same length. The diagonal of a square is greater in length than its side.
If two squares have the same perimeter, will they have the same area?
Yes, if two squares have the same perimeter, it means that they also have sides of the same length. This, in turn, implies that they also have the same area.



























