Diagonal of a Square – Definition, Formula, Properties, Examples

What Is the Diagonal of a Square?

Diagonals of a square are the line segments joining opposite vertices.

A flat, closed shape with four equal sides, four vertices (like craft paper, a photo frame), and four right angles is known as a square. Take a look at the square craft paper shown below. Let’s connect two opposite corners. The two lines are called diagonals of a square.

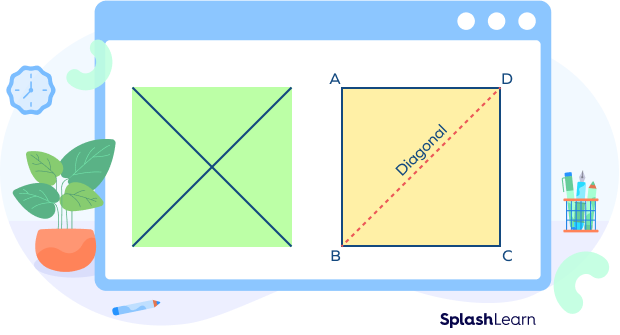
Diagonal of a Square Definition

The diagonal of a square is a line that connects one corner to the opposite corner through the center. In other words, we can say that the diagonal is the slant line that connects the square’s opposite corners.

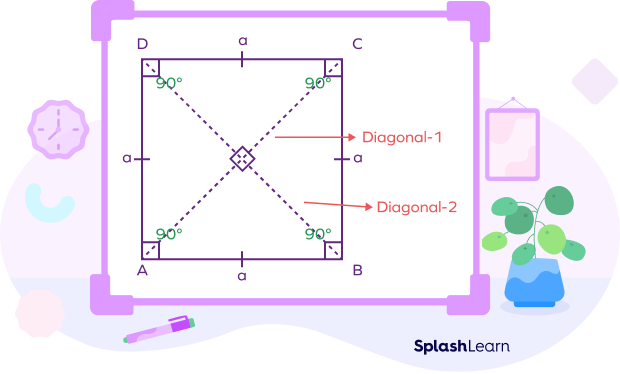
A square has two diagonals that are equal in length. They bisect each other at right angles.

Properties of the Diagonal of a Square

• The diagonal of a square is a line segment that connects any two non-adjacent vertices (corners).

Here, AC and BD are diagonals.

• The diagonals of a square are equal in length.

$AC = BD$

• The square is divided into two congruent right-angle isosceles triangles by its diagonal.

• Two diagonals of a square bisect each other at right angles.

• When the diagonals meet the vertices of a square, they form a 45-degree angle. In other words, they bisect each pair of opposite angles.

• Pythagoras’ theorem can also be used to determine the length of the diagonals of a square.

Diagonal of a Square Formula

The formula for the diagonal of a square is given by the product of side length and the square root of 2.

Mathematically, the diagonal of a square formula is given by

$d = a\times\sqrt{2} = \sqrt{2} a$

where, 

$d =$ length of diagonal of a square 

$a =$ side length of the square.

Derivation of Diagonal of Square Formula

Let’s derive the diagonal of a square formula.

Let us assume that the side length of a square is “a” and the length of the diagonal is “d.”

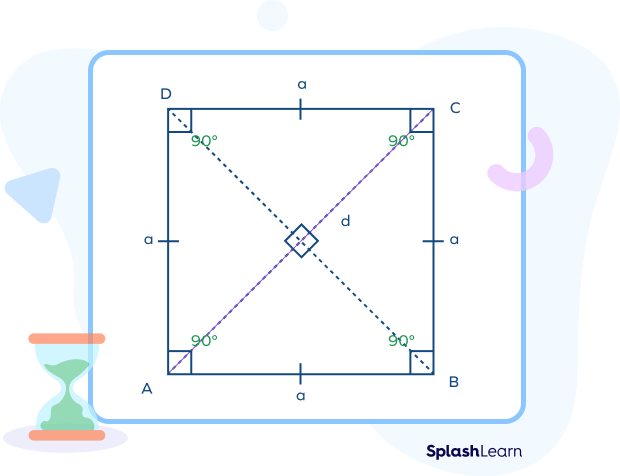
In the above figure, a square is divided into two right-angle triangles. Let’s consider triangle ABC.

In $\Delta ABC,\; \angleB = 90^\circ$. 

Note that the diagonal AC acts as a hypotenuse of the right triangle ABC.

So, now in $\Delta ABC$ apply Pythagoras’ theorem,

$AC^2 = AB^2 + BC^2$

$d^2 = a^2 + a^2$

$d^2 = 2a^2$

$d = \sqrt{2a^2}$

$d = a\sqrt{2}$

Hence, diagonal “d” of square is given by $d = a\sqrt{2}$

where “d” is the diagonal length and “a” is the side-length of the square.

How to Find the Diagonal of a Square

How to calculate the length of diagonal of a square? What is the diagonal measurement of a square? Finding the diagonal of a square is simple once you know the formula! Use the diagonal of a square formula. Multiply the length of the side by $\sqrt{2}$.

Length of the diagonal of a square $=$ Length of the side of the square $\times\sqrt{2}$

To get an estimate, we can use $\sqrt{2}\simeq 1.41$.

Methods to Calculate Diagonal of Square

The diagonal of a square can be calculated in three different ways.

Method 1: When the Side-Length of Square Is Given

If the length of one side of the square is known to us, then we can simply calculate the diagonal of a square using the formula $d = a\sqrt{2}$.

Where, d = length of diagonal of a square and a $=$ side length of the square.

Method 2: When the Perimeter of Square Is Given

If the perimeter of a square is given or known to us, then follow the below steps

• First find the side length (a) of the square by using the perimeter of the square formula. 

Perimeter of a square$ = 4\times a$.

Side of the square $= \frac{Perimeter}{4}$

• Calculate the diagonal of the square using the formula: $d = a\sqrt{2}$

Method 3: When the Area of a Square Is Given

If the area of a square is given or known to us, then follow the below steps:

• First find the side length (a) of the square by using the area of square formula. 

Area of a square $= a^2$

Side of the square $= \sqrt{Area} = a$

• Calculate the diagonal of the square using the formula $d = a\sqrt{2}$.

Facts about Diagonals of a Square

• The diagonal of a square is longer than its side.

• A square has four lines of symmetry, one vertical, one horizontal, and two diagonal lines.

Conclusion

In this article, we learned about the diagonal of a square formula, its properties, formula, derivation, different methods to calculate the length of a diagonal if the side length is given, and related facts, examples, and practice problems based on the same.

Solved Examples on Diagonals of a Square

1.  Find the diagonal length of a square with 18 inches of side.

Solution:

The side length of the square “a” $= 18$ inches.

According to the diagonal of square formula,

The diagonal length “d” of the square $= a\sqrt{2} = 18\times\sqrt{2} = 18\times1.414 = 25.42$

Hence, the diagonal length of the square is 25.42 inches.

2. The length of the diagonal of a square is $15\sqrt{2}$ inches. Find the side length of its side.

Solution:

The diagonal length of the square $= d = 15\sqrt{2}$ inches.

Let us consider the side length of the square to be “a.”

The diagonal length “d” of the square $= a\sqrt{2}$

$15\times\sqrt{2} = a\sqrt{2}$

Comparing both sides, we get

$a = 15$

Hence, the side length of the square is 15 inches.

3. Find the diagonal length of a square field with a perimeter of 124 feet.

Solution:

The perimeter of the square $= 124$ feet

Let us consider the side length of the carrom board to be “a.”

As we know, the perimeter of the square $= 4a$

$124 = 4a$

$a = \frac{124}{4} = 31$

Thus, $a = 31$ feet

Diagonal length $= d = a\sqrt{2} = 31\times\sqrt{2} = 43.83$ feet.

Hence, the diagonal length of the square field is 43.83 feet.

4. Find the length of the diagonal of a craft paper if its area is 196 square units.

Solution:

The Area of the craft paper $= 196$ square units

As we know craft paper is in the shape of a square.

The area of a square $= a^2 = 196$

Side length $= a = \sqrt{196} = 14$ units.

The diagonal length of the square $= d = a\sqrt{2} = 14\times\sqrt{2} = 19.8$ units.

Hence, the length of the diagonal of the craft paper is 19.8 units.

Practice Problems on Diagonals of a Square

Frequently Asked Questions on Diagonals of a Square