Perimeter of a Square – Introduction
In geometry, the perimeter of a shape is defined as the total length of its boundary. The perimeter of a square is determined by adding the length of all the sides. It is measured in linear units of measurement like centimeters, meters, inches, or feet.
Recommended Games
What is the Perimeter of a Square?
The perimeter of a square is the total length of all the sides of the square. Hence, we can find the perimeter of a square by adding all its four sides.
All the sides of a square are equal. So, the perimeter of a square is calculated by adding the side of a square four times.
Recommended Worksheets
Perimeter of a Square Formula
To calculate the perimeter of a square, we use the following formula:
P $= 4 \times$ side $=$ 4a
Derivation of Perimeter of Square Formula
| Perimeter of general quadrilateral | $= $Sum of the sides |
| $= a + b + c + d$ where a, b, c, and d are sides of the quadrilateral |
Since the sides of a square are equal, that means, $a = b = c = d$
This means,
| Perimeter of square | $= a + a + a + a$ |
| $= 4 \times a$ |
If we have a square with each side measuring 14 feet, then the perimeter of a square is given by $4 \times 14$ feet $= 56$ feet.
How to Find the Perimeter of a Square?
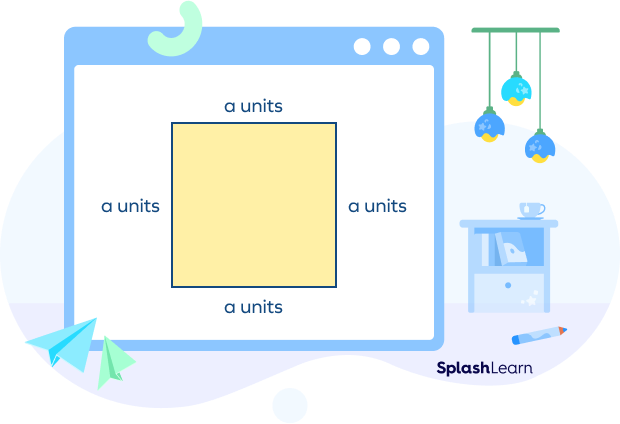
We can find the perimeter of a square with side ‘a’ units by adding the lengths of all sides.
So, we add the side length ‘a’ four times.
Perimeter of a square $= (a + a + a + a)$ units
Perimeter of a square $= (4\times a)$ units
Finding Perimeter of a Square when the Side is Unknown
Other than the side, we can find the perimeter of a square if we know its area. Let’s find out how.
Let’s consider a square with area A sq. units.
We know that area $= side^2$
So, using the area we can find the side of the square as $\sqrt{A}$.
And then we can use the measurement of the side to find the perimeter of the square.
Let us suppose we have to find the area of the square whose area is $36 \text{cm}^2$.
To find the perimeter of a square using the area, we can use the steps given below:
- Step 1: Find the side length using the area with the formula side $=$ A. In this example, side $= \sqrt{36} = 6$ cm
- Step 2: Apply the perimeter formula of the square, i.e., $4 \times$ side $= 4 \times 6 = 24$ cm
We can directly use the area to find the perimeter using this formula.
Perimeter of the square $= 4 \times (\sqrt{area}) = 4\sqrt{area}$ units.
Solved Examples On Perimeter of a Square
1. What will be the perimeter of the square whose side is 10 cm?
Solution: Here, the side of the square $= 10$ cm
We know that perimeter of a square $= 4 \times$ side
So, the perimeter of the square with side $10$ cm $= 4 \times 10 = 40$ cm
2. If the area of the square is $144$ m2, what will be the perimeter?
Solution: Here, the area of square $= 144$ m2
We know that perimeter of the square whose area is given $= 4\sqrt{area}$
Perimeter of the square $= 4 \times \sqrt{144} = 4 \times 12$ m $= 48$ m
3. If the perimeter of a square is 56 cm, what will be the side of the square?
Solution: Here, the perimeter of square $= 56$ cm
We know that side of the square when perimeter is given = Perimeter$\div 4$So, the side of a square with perimeter 56 cm $= 56\div4 = 14$ cm
Practice Problems On Perimeter of a Square
Perimeter of a Square
Andy wants to frame 4 pictures. The pictures are square shaped, each side equal to 7 cm. Find the total length of the wooden sticks required to make the frames.
Side of 1 picture $= 7$ cm
Frame required for one picture $=$ Perimeter of the 1 picture $= 4 \times 7 = 28$ cm
Frame required for 4 pictures $= 4 \times 28 = 112$ cm
Mary is building a square-shaped enclosure for her rabbit. Each side of the enclosure measures 15 m. Find the length of fence required, if Mary wants to fence from all 4 sides.
Side of the square enclosure $= 15$ m
Fence required for enclosure = Perimeter of the square enclosure $= 4 \times 15 = 60$ m
The area of the square field is $81 \text{ft}^2$. What will be the cost of fencing the field if 1 foot costs $\$$2.5?
Area of the square field $= 81 \text{ft}^2$
Perimeter of the square $= 4\sqrt{area} = 4 \times \sqrt{81} = 4 \times 9 \text{ft} = 36 \text{ft}$
Frequently Asked Questions On Perimeter of a Square
How is the perimeter of a square different from the area of the square?
Perimeter of the square is the total length of the boundary of a square. On the other hand, the area of the square is the space occupied by the boundary of the square.
What is the use of the perimeter in daily lives?
We often use the concept of perimeter in real life. For example, when we want to put a fence around the backyard, we find its perimeter to know the length of wire we will need.
Why is the unit of perimeter the same as the unit of its side?
Perimeter is the sum of all the sides of the shape. This means it represents the total length of the boundary. So, its unit will also be a unit of length same as the unit of the sides of the shape.



























