What Is a Meter in Math?
Today, Jo had a medical test at her school. After the examination, she went to her classroom, where her peers discussed their height. “My height is 126 cm,” exclaimed Tom. “Mine is 51 inches,” said Lily. “I’m 3.4 feet,” claimed Harry. Jo was confused. She knew her height only in meters.

Recommended Games
Meter Definition
The meter is the standard unit of measuring length in the International System of Units (SI). Its symbol is “m” and it is one of the seven base units of the SI system.
What does ‘m’ stand for in math?
We use it to express length or distance. For instance, the length of the Eiffel Tower is 330 m.

You might have noticed that while talking about their heights, Tom uses centimeters, Lily uses inches, and Harry uses feet. While miles and yards may be used to measure the length of a park, meters or feet are used to measure the height of a building or a mountain peak.
But why is it given such importance around the world? The answer is simple. Inches and feet are two customary length units and are not the same everywhere. For instance, one inch is 2.54 cm in the US, 3.33 cm in China, and 2.61 cm in Norway. Therefore, the SI units and the metric system were created; they remain the same throughout the world.
In the metric system, too, the meter is the most important unit. Why? Let’s take centimeters. “Centi” means one-tenth. One centimeter is one-hundredth of a meter, where the meter is the reference unit. In other words, all the units in the metric system are multiples or submultiples of a meter.
Recommended Worksheets
Fun Fact!
The meter is the reference unit for other units in the metric system. But what is the length of a meter? From pendulums to meter bars, we have come a long way in defining a meter. Today, a meter is the distance traveled by light in 129,97,92,458 of a second.
Let’s now look back and see what was the definition of meter in the past.
- Before 1793, a meter was the length of a second pendulum.
- In 1793, it was one ten-millionth of the distance from the equator to the North Pole along the great circle.
- From 1795 to 1960, standard meter bars were used as a reference to define the length of a meter.
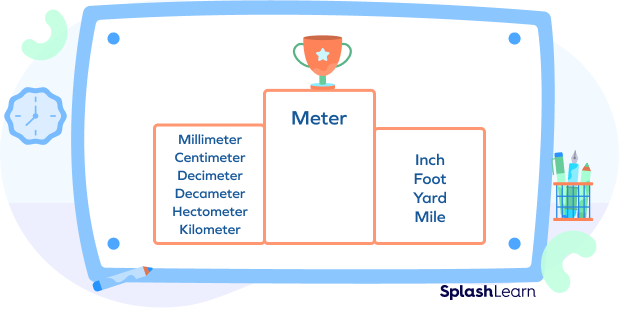
Meter and Other Units of Measuring Length
We saw that Tom, Lily, and Harry used different units to express their height. Now, who is the tallest? Because it is difficult to compare heights in different units, we have to convert all into any one unit and compare them.
Since we saw that the meter is the most important unit of length, let’s see how we can convert different units into it. For that, let’s make a conversion table.
| Units | Meaning | Relationship with one meter |
| Millimeter | “Milli” means one-thousandth. Therefore, a millimeter is one-thousandth of a meter. | 1 mm $= 0.001$ m |
| Centimeter | “Centi” means one-hundredth | 1 cm $= 0.01$ m |
| Decimeter | “Deci” means one-tenth | 1 dm $= 0.1$ m |
| Decameter | “Deca” means ten times | 1 dam $= 10$ m |
| Hectometer | “Hecto” means hundred times | 1 hm $= 100$ m |
| Kilometer | “Kilo” means thousand times | 1 km $= 1,000$ m |
Now, what is the relationship between a meter and customary units of length? The International Yard and Pound Agreement in 1959 defined one yard as 0.9144 m.
We know that 1 yd $= 3$ ft $= 36$ in (as 1 ft $= 12$ in)
So, 0.9144 m $= 3$ ft, 1 ft $= 0.3048$ m
Also, 0.9144 m $= 36$ in, 1 in $= 0.0254$ m
Similarly, 1 mi $= 1760$ yd. So, 1 mi $= 1760 \times 0.9144 = 1,609.344$ m
So, the relationship between meters and customary units of length are:
| Units | Relationship with meters |
| Inch | 1 in $= 0.0254$ m |
| Foot | 1 ft $= 0.3048$ m |
| Yard | 1 yd $= 0.9144$ m |
| Mile | 1 mi $= 1609.344$ m |
Solved Examples
1. Express Tom’s height in meters.

Solution: Tom’s height is 126 cm.
We know that 1 m $= 100$ cm.
Tabulating what we know, we get:
| 1 m | 100 cm |
| x m | 126 cm |
On cross-multiplying,
$100x = 126$
$x = 1.26$ m
Therefore, Tom’s height is 1.26 m.
2. Express Lily’s height in meters.

Solution: Lily’s height is 51 inches.
We know that 1 in $= 0.0254$ m. Tabulating what we know, we get:
| 1 in | 0.0254 m |
| 51 in | x m |
On cross multiplying,
$0.0254 \times 51 = x$
$x = 1.29$ m.
Therefore, Lily’s height is 1.29 m.
3. Express Harry’s height in meters.

Solution: Harry’s height is 3.4 ft.
We know that 1 ft $= 0.3048$ m. Tabulating what we know, we get:
| 1 ft | 0.3048 m |
| 3.4 ft | x m |
On cross multiplying,
$x = 3.4 \times 0.3048 = 1.03$ m.
Therefore, Harry’s height is 1.03 m.
Practice Problems
Meter
Express 1.24 mi in ‘m’.
We know that 1 mi $= 1609.344$ m
On cross multiplying,
$x = 1609.344 \times 1.24 = 1995.5$ m ~ 2000 m.

The side of a square with an area of 1 sq. m is:

Area of a square $= \text{side} \times \text{side}$
Let the side be y
$1 = y \times y$
$1 = y^2$
$y = 1$
Side of the cube $= 1$ m $= 100$ cm.
The height of a tree is 0.15 decametres. Its height in ‘m’ is:

We know that 1 dam $= 10$ m. Tabulating what we know, we get:
On cross multiplying,
$x = 0.15 \times 10 = 1.5$ m
Therefore, the height of the tree is 1.5 m.

Frequently Asked Questions
The meter became legal in the US in 1866, although it’s still not standard to use the meter.
What is the relationship between meter and liters?
One cubic meter equals 1000 liters. Understand that 1 cubic meter is the volume of a cube having 1 m side length. So, we can say that a cube with side 1 m can hold 1000 liters of water.
How many meters are there in a statute mile?
A statute mile is 1609 m.




































