Irregular Polygons Introduction
We know that a polygon is a two-dimensional enclosed figure made by joining three or more straight lines. A regular polygon is a type of a polygon that has equal sides and all interior angles of equal measure. If any one of the conditions is not met, it becomes an irregular polygon. Check out the irregular polygon shapes based on three conditions.
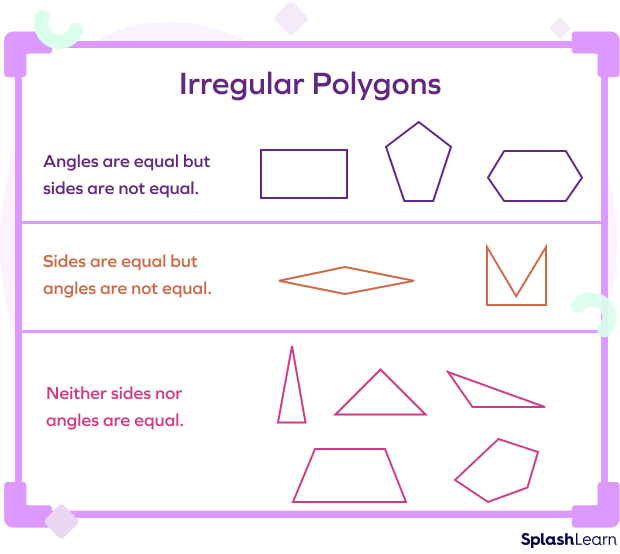
Note that non-polygon shapes are the shapes that do not fulfill the criterion of a polygon. For example: Circle
Recommended Games
What Are Irregular Polygons?
Irregular polygons are polygons that do not have equal sides and equal angles.
Common examples of irregular polygons are a scalene triangle, kite, rectangle.
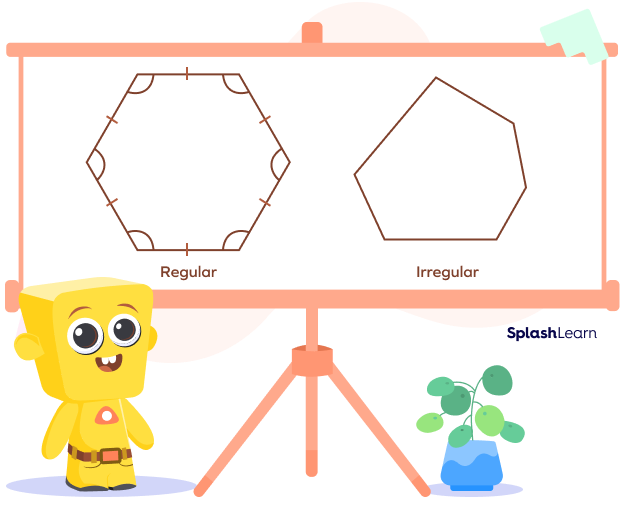
The image below shows the difference between a regular hexagon and an irregular hexagon.
Irregular Polygons: Definition
A polygon is said to be an irregular polygon or non-regular polygon if all the sides are not equal in length and and all the interior angles may not be of equal measure.
How to Classify Irregular Polygons
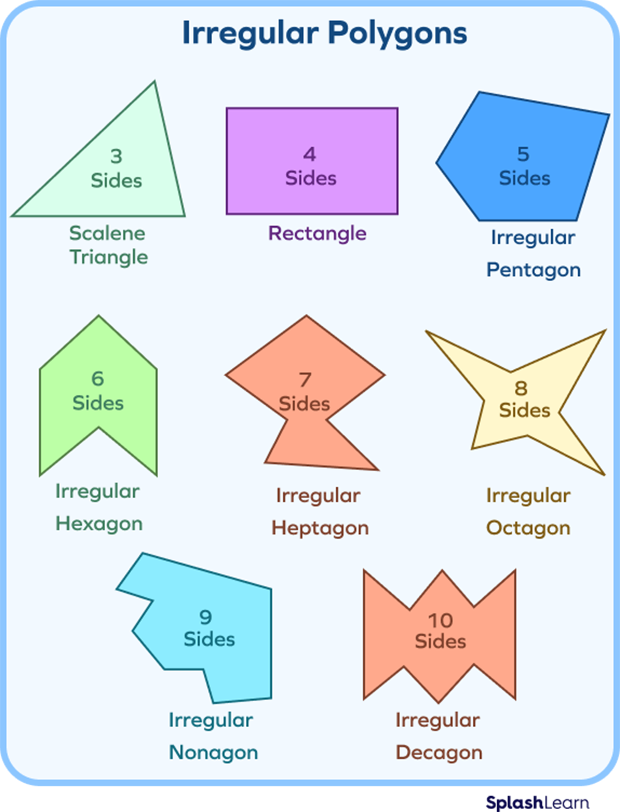
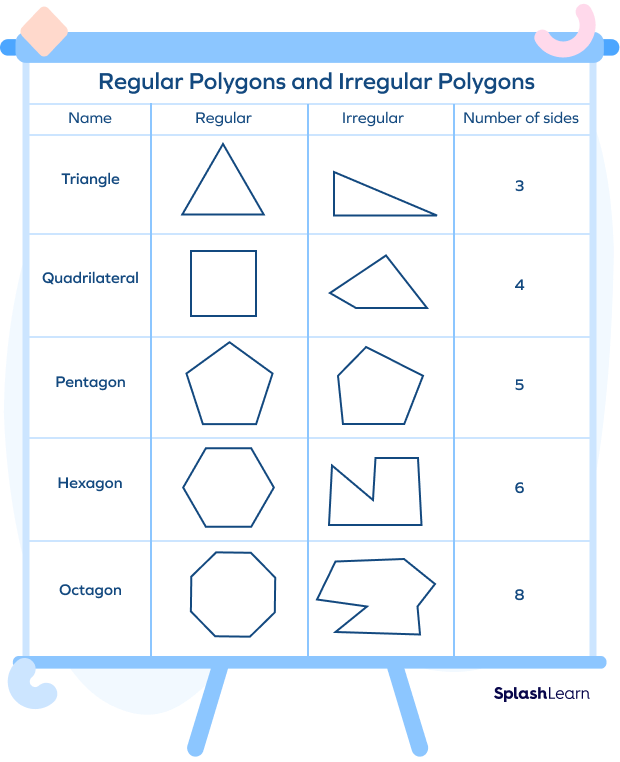
We can classify irregular polygons based on the number of sides. A three-sided polygon is a triangle, a four-sided polygon is a quadrilateral, a five-sided polygon is a pentagon, and so on. Here are a few examples showing the names of irregular polygons and the number of sides:
Properties of Irregular Polygons
Let’s see some properties of irregular polygons.
- First, a regular polygon has equal sides and equal angles. If the polygon fails to meet one of these two conditions, it becomes an irregular polygon.
- Second, there are irregular polygons having equal sides but unequal angles and vice versa.
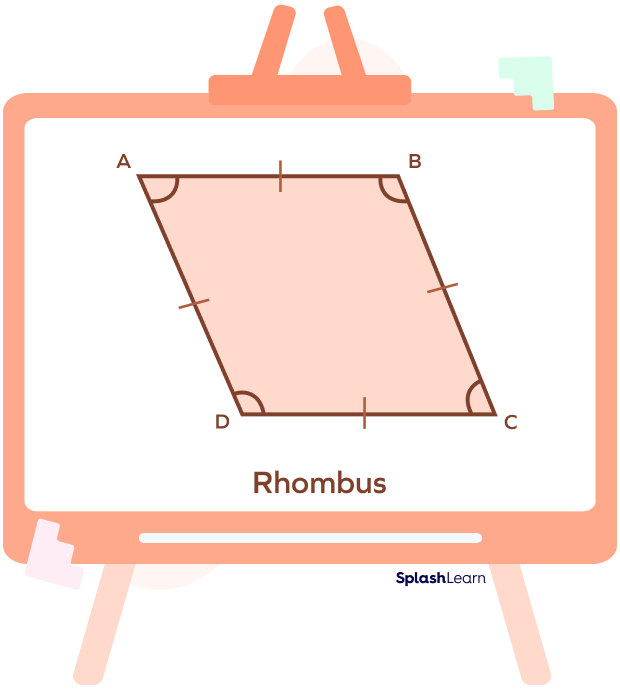
- In the figure shown below, the shape is a rhombus. Is a rhombus a polygon? Yes, because it is a closed figure made of four line segments. A rhombus is an irregular polygon with equal sides and unequal angles. Its opposite angles are equal but all angles do not have the same measure.
In the above figure, shape B is a rectangle. Now, is a rectangle a polygon? Yes, it is, as it is a closed figure made of line segments. However, it is an irregular polygon with equal angles (90 degrees each) and unequal sides.
Common Types of Irregular Polygons
We will discuss some common irregular polygon examples along with their important properties.
Scalene Triangle
A scalene triangle has three unequal sides. So, it is an irregular polygon.
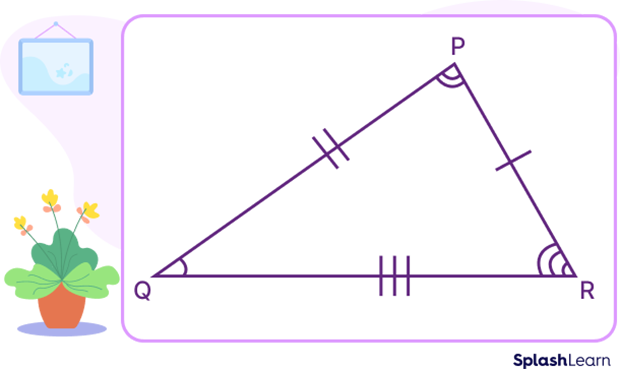
In the figure, the scalene triangle PQR is an irregular polygon as PQ, QR, and PR are of different lengths.
Isosceles Triangle
An isosceles triangle has two equal sides $(\text{AC} = \text{AB})$ and two equal angles (angle C $=$ angle B). Since the third side and the third angle are not equal to the other two, it is an irregular polygon.

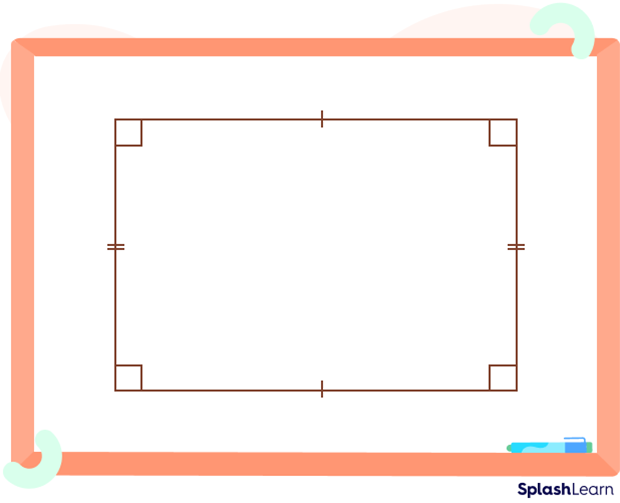
Rectangle
A rectangle ABCD has congruent angles (all angles are right angles), but it does not have equal sides. Since only the opposite sides are equal, a rectangle is an irregular polygon.
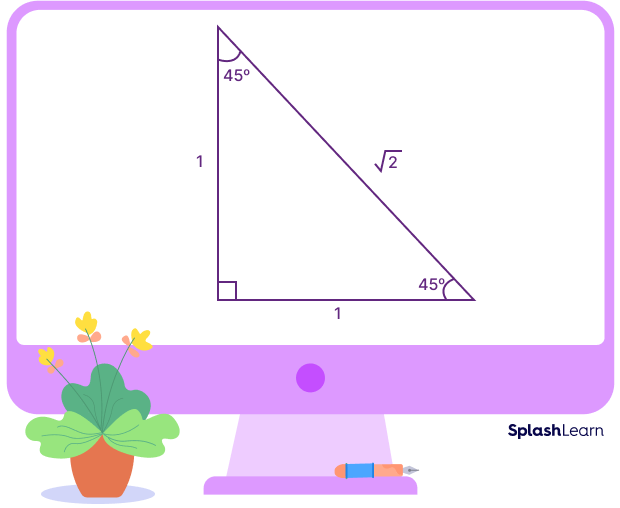
Right Triangle
In the right triangle ABC, if the angle B is right angle, the angles A and B will be acute angles (the sum of all angles of a triangle is 180 degrees). Therefore, the three angles cannot be congruent. So, it is an irregular polygon. The following image shows an example of one such right triangle.
Irregular Pentagon
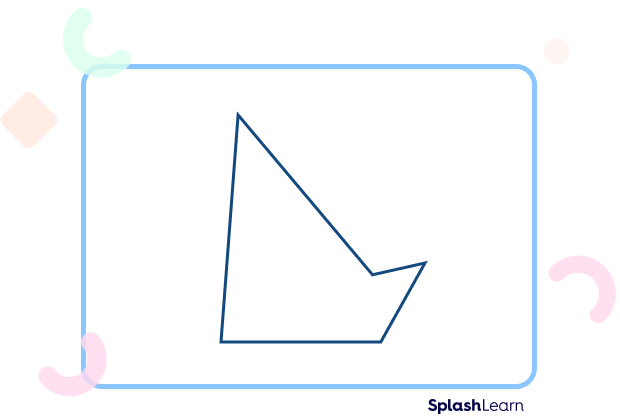
An irregular pentagon is a polygon with five unequal sides. Since it does not have equal sides, it is an irregular polygon.
Irregular Hexagon
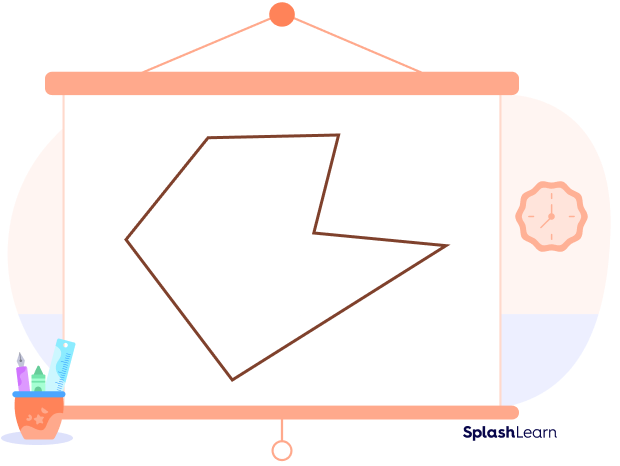
An irregular hexagon (or a non regular hexagon) has six unequal sides. So, a non-regular hexagon is an irregular polygon.
Formulas Associated with Irregular Polygons
There are three formulas related to irregular polygons: area formula, perimeter formula, and angle-sum formula.
Area of Irregular Polygons
Since irregular polygons come in different shapes and sizes, we do not have a standard formula for finding the area of an irregular polygon. So, we can divide it into regular polygons for which the area can be calculated and then we can add them to get the area of an irregular polygon.
In the following figure, the irregular polygon can be divided into two triangles PQM and RSN, and a rectangle PQRS.
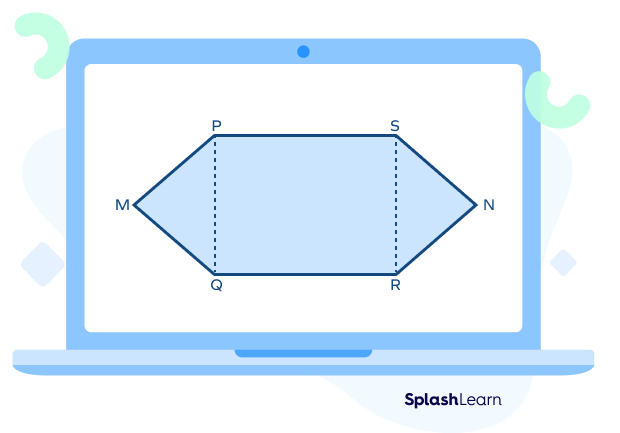
So, the area of the given irregular polygon $=$ Area of $\angle$PQM $+$ Area of $\angle$RSN $+$ Area of rectangle PQRS
We can find the area of a triangle, provided that the base and height is known, by the formula:
Area of a triangle $= \frac{1}{2}$ base $\times$ height.
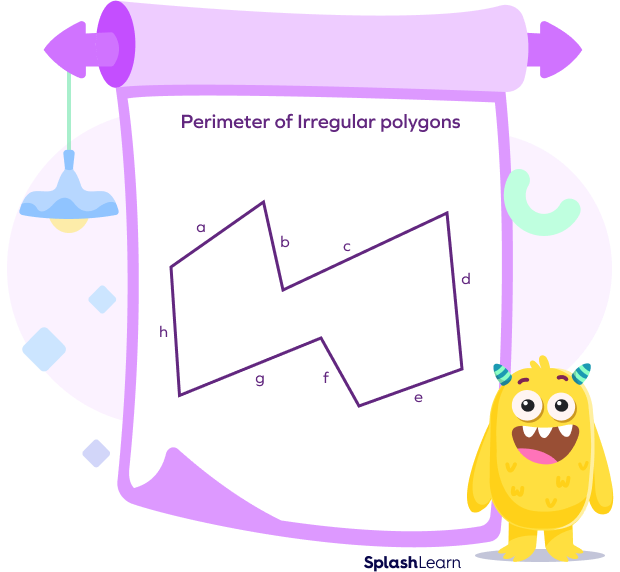
Perimeter of Irregular Polygons
To find the perimeter of an irregular polygon, we have to add up the length of all its sides.
Consider the irregular polygon given below. The side lengths are a, b, c, d, e, f, g, h.
Perimeter $= a + b + c + d + e + f + g + h$
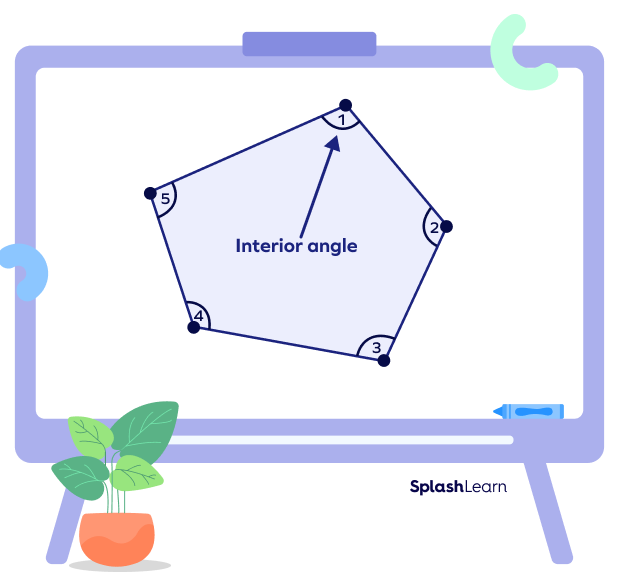
Interior Angles and Exterior Angles
When you extend a side of an irregular polygon, the angle formed between the extended side and its adjacent side is the exterior angle. On the other hand, interior angles are angles between a polygon’s two adjacent sides.
Sum of Interior Angles of Irregular Polygons
The interior angle-sum formula for an irregular polygon is the same as the sum of interior angle in a regular polygon.
Sum of interior angles in a n-sided polygon $= (n − 2) 180^{\circ}$, where n is the number of sides of the irregular polygon.
Example: What is the sum of the interior angles in a pentagon?
Solution: A pentagon has 5 sides.
So, $n = 5$
The sum of interior angles of a regular polygon $= (5 − 2) \times 180^{\circ}$
$= (5 − 2) \times 180^{\circ}$
$= 3 \times 180$
$= 540^{\circ}$
Therefore, the sum of interior angles of a pentagon is $540^{\circ}$.
Sum of Exterior Angles of Irregular Polygons
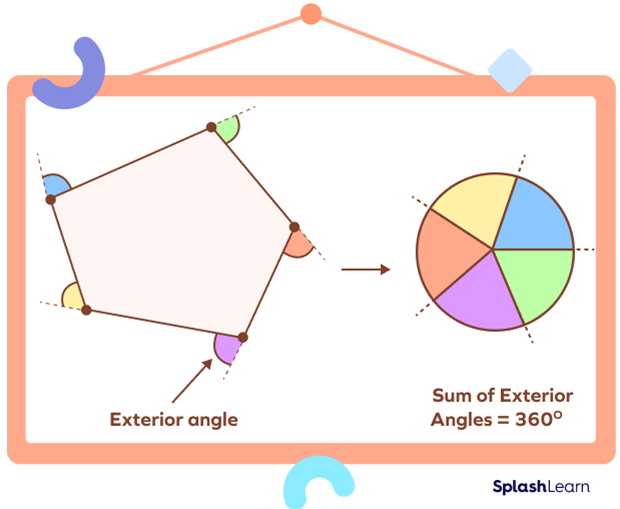
For any polygon, regular or non-regular, the sum of its exterior angles is 360 degrees.
Regular Polygons vs. Irregular Polygons
Let’s now compare and contrast regular and irregular polygons.
- All sides of a regular polygon are congruent.
Irregular polygons generally don’t have equal sides.
Rhombus is an example of an irregular polygon; it has equal sides, but unequal angles.
- Regular polygons have equal interior/exterior angles.
In irregular polygons, the measure of all interior/ exterior angles is not equal.
A rectangle is an example of an irregular polygon where all the angles are equal but all sides are not of equal length.
- Regular polygons have equal sides and equal angles. Conversely, irregular polygons can either have equal sides or equal angles or none.
Solved Examples
1. Find the perimeter of the below figure:
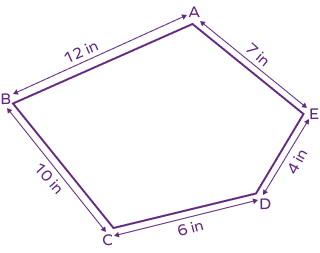
Solution:
The perimeter of the irregular pentagon $ABCDE = AB + BC + CD + DE + AE$
$= 12 + 10 + 6 + 4 + 7$
$= 39$ inches
2. Find the area of the below right triangle ABC.
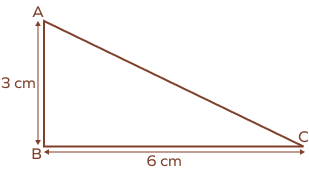
Solution:
Area of the right triangle ABC $= \frac{1}{2} \times$ base $\times$ height
$= \frac{1}{2} \times$ BC $\times$ AB
$= \frac{1}{2} \times 6 \times 3$
$= 9$ $\text{cm}^{2}$.
3. How many exterior angles are there in an irregular octagon?
Solution: An irregular octagon has eight sides and eight interior angles. Therefore, it has eight exterior angles because the number of interior angles of a polygon is equal to its exterior angles.
4. Find the sum of the interior angles of a polygon with eleven sides.
Solution: The sum of interior angles of an n-gon is $(n − 2) \times 180^{\circ}$.
Here, $n = 11$.
So, interior angle sum $= 9 \times 180^{\circ} = 1620^{\circ}$ degrees.
5. If the sum of the interior angles of an irregular polygon with “n” sides is 1800 degrees, what is n?
Solution: Given the sum of the interior angles of an n-gon $= 1800^{\circ}$
$(n − 2) × 180^{\circ} = 1800^{\circ}$
$n − 2 = 10$
So, $n = 12$.
Therefore, the polygon has 12 sides.
Practice Problems
Irregular Polygons
The sum of interior angles of an irregular octagon is:
Sum of interior angles of an irregular polygon $= (n - 2) \times 180^{\circ}$
An octagon has 8 sides. So, $n = 8$
$(n - 2) \times 180^{\circ} = (8 - 2) \times 180^{\circ} = 6 \times 180^{\circ} = 1080^{\circ}$
The sum of exterior angles of an irregular triangle is:
The sum of exterior angles of all polygons is $360^{\circ}$.
The rhombus is irregular since it has
All sides of a rhombus are equal. Its opposite angles are equal.
A rectangle is irregular because:
A rectangle is an irregular polygon. All angles of a rectangle are right angles, and thus congruent. However, all sides of a rectangle are not equal; only opposite sides are congruent.
Which of the following triangles is not an irregular polygon?
Equilateral triangle has all sides congruent and all angles measure $60^{\circ}$. So, it is a regular polygon.
Frequently Asked Questions
What are non-polygon shapes?
Non-polygon shapes are figures that do not satisfy the conditions of being polygon. Examples can be a circle and open shapes.
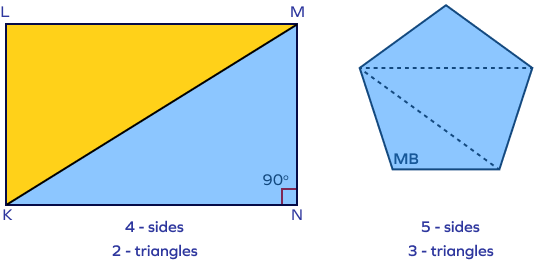
How many triangles are required to form a polygon?
The number of triangles required to form a polygon is equal to the number of sides of a polygon minus two. If the polygon has “n” sides, then the number of triangles in a polygon is $(n – 2)$. For examples, to form a rectangle (which has 4 sides), we need $4 – 2 = 2$ triangles.
What is the difference between an equilateral irregular polygon and an equiangular irregular polygon?
Equilateral irregular polygons are irregular polygons that have equal sides but not equal angles. Conversely, equiangular irregular polygons are irregular polygons with equal angles but not equal sides.
Is a parallelogram a regular polygon?
Parallelograms like rhombus and rectangles are irregular polygons, whereas a square, also a parallelogram, is a regular polygon.
What is the sum of an irregular polygon’s interior and exterior angles at the same corner?
The interior angle and exterior angle of an irregular polygon at the same corner have a sum of 180 degrees (as it falls on a straight line).






















