Equiangular Triangle: Introduction
Equiangular triangle is a triangle in which angles are congruent and all sides are of equal length. It is often called an equilateral triangle. It is a regular polygon with three equal sides and the angles of the same measure.
Recommended Games
Equiangular Triangle: Definition
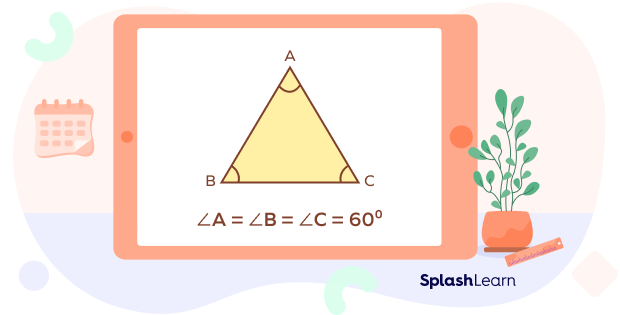
A triangle with three equal interior angles is called an equiangular triangle. In an equiangular triangle, the measure of each of its interior angles is 60 ̊.
Recommended Worksheets
What Is an Equiangular Triangle?
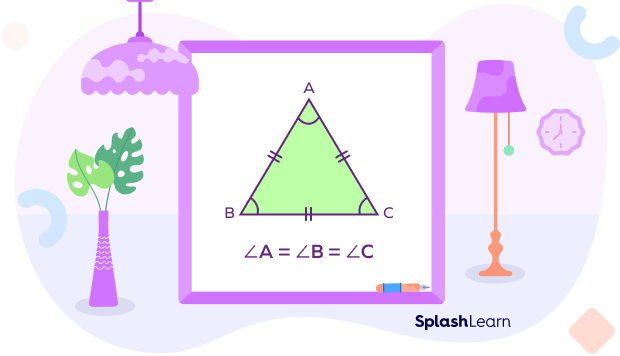
In an equiangular triangle, all interior angles are of equal measure. Thus, all its three sides are also of equal length. It is the same as an equilateral triangle.
Non-examples of Equiangular Triangle
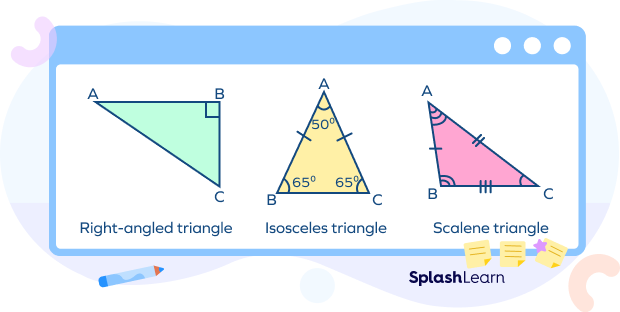
In the given non-examples, all the figures are of triangles, but none of them is an equiangular triangle because:
- In a right-angled triangle, one of the interior angles is $60^\circ$.
- In an isosceles triangle, only two interior angles are equal.
- In a scalene triangle, none of the interior angles is equal.
For a triangle to be equiangular all its three interior angles must be equal, that is, each angle should measure $60^\circ$.
Properties of Equiangular Triangles
Triangles have different classifications depending on their properties, angles, and sides. We have different triangles, such as an isosceles triangle or a right triangle. An equiangular triangle has its own properties based on the angles and sides. The properties of an equiangular triangle are:
- An equiangular triangle has all the three sides congruent to each other.
- All three angles are equal to each other and measure at $60^\circ$ each.
- Since the angles of an equiangular triangle are always $60^\circ$, the triangle is always an acute-angled triangle.
- The radius of an incircle in an equiangular triangle is considered exactly half of the radius of a circumcircle.
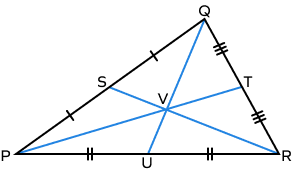
- In an equiangular triangle, an orthocenter and centroid are all considered to be the same points.
How to Construct an Equiangular Triangle?
An equiangular triangle can be constructed just by using a compass and a ruler. Since the sides of the triangle are equal in length, construction becomes very simple. Here are the steps to draw an equiangular triangle:
Step 1: Draw a line segment AB, which will be considered as the length of the sides of the triangle.
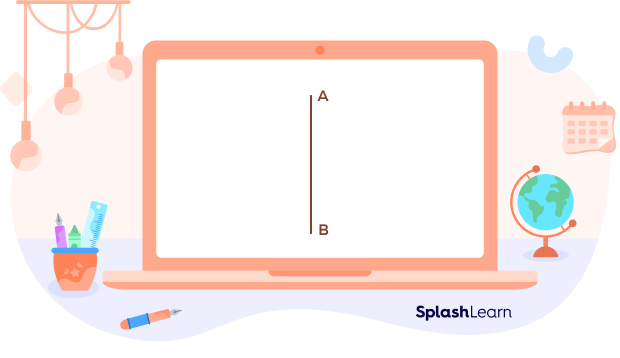
Step 2: Mark a point X anywhere that will be one vertex of the triangle.
Step 3: Measure the length of line segment AB with a compass. With one point of the compass at A and the drawing part of the compass at B.
Step 4: With the obtained length, keeping the compass at point X marks two arcs from the drawing end without changing the length of the compass.
Step 5: These two arcs will be considered the other two vertices of the triangle.
Step 6: On the second arc, mark a point Y. It could be any of two arcs.
Step 7: Place the compass on point Y, and draw arcs crossing the third arc creating the point Z.
Step 8: Using a ruler, join all the points creating an equiangular triangle.
Perimeter of an Equiangular Triangle
Perimeter of an equiangular triangle is considered as the sum of all sides or three times of a side since all the sides are equal to each other. Hence, the formula to calculate the perimeter is given as:
Perimeter $= 3 \times a$,
where a is the side.
Area of Equiangular Triangle
The area of an equiangular triangle is the space covered within the perimeter or three sides of the equiangular triangle and is expressed in square units. Some important units used to express the area are sq. in, sq. m, sq. cm, sq yd, etc. The formula to calculate the area of an equiangular triangle is given as:
Area $= \sqrt{\frac{3}{4}} (side)^2$ square units
Conclusion
In this article, we learned about equiangular triangles. We saw their properties and understood ways of construction. Let us now look at some examples and solve practice problems based on area and perimeters.
Solved Example
1. What is the angle opposite to the side AB if ABC is an equiangular triangle?
Solution:
All the angles of an equiangular triangle measure the same, i.e., $60^\circ$.
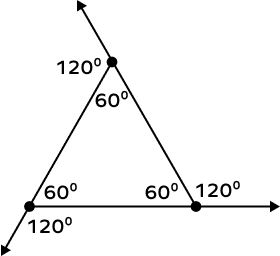
2. What is the measure of exterior angle of an equiangular triangle?
Solution:
The measure of exterior angle of an equiangular triangle is:
We know that sum of angle on a strength line is $180^\circ$,
Now
$Interior angle + Exterior angle = 180^\circ$
$60^\circ + Exterior angle = 180^\circ$
$Exterior angle = 180^\circ – 60^\circ$
$Exterior angle = 120^\circ$
3. What is the sum of angles of an equiangular triangle?
Solution:
The sum of angles of a triangle is always 180 degrees.
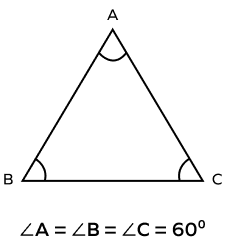
$\angle \text{A} + \angle \text{B} + \angle \text{C} = 60^\circ + 60^\circ + 60^\circ = 180^\circ$
4. In an isosceles triangle, the equal sides measure 4 inches and all the angles measure $60^\circ$. Find out the length of the other side.
Solution:
We observe that since all the angles measure $60^\circ$. So, the triangle is not isosceles but equiangular.
Hence, the other side measures the same as given two equal sides, i.e., 4 inches.
5. What is the perimeter of an equiangular triangle of sides measuring 5 inches?
Solution:
Perimeter of equiangular triangle $= 3 \times side$
$= 3 \times 5$ inches
$= 15$ inches
Practice Problems
Equiangular Triangle - Definition with Examples
What is the perimeter of an equilateral triangle with a side equal to 10 cm?
Perimeter $= 3 \times \text{sides of equilateral triangle}$
Perimeter $= 3 \times 10 = 30 cm$
What is the perimeter of an equiangular triangle where each side is 6 inches?
The formula to calculate the perimeter is:
Perimeter of equilateral triangle $= 3a$, where a is the side.
Given, $a = 6$ inches.
Thus, perimeter $= 3 \times 6= 18$ inches.
Therefore, the perimeter of the equiangular triangle is 18 inches.
What is the area of the equilateral triangle ABC, where AB $=$ AC $=$ BC $= 9$ cm?
By the formula, we know;
Area $= \sqrt{\frac{3}{4}}$ $a^2$
Given a $= 4 cm$
Hence, by putting the value we get;
Area $= \sqrt{\frac{3}{4}}$ $(4 cm)^2$
Area $= \sqrt{\frac{3}{4}}$ $16 cm^2$
Area $= 6.92$ sq. cm
What is the altitude of an equilateral triangle whose sides are equal to 12 cm.
By the formula, we know,
Height of an equilateral triangle $= \sqrt{\frac{3a}{2}}$
Since, $a = 12 cm$
Hence,
h $= \sqrt{3} \times \frac{12}{2}$
h $= 6\sqrt{3}$
Abel is eating a large triangular-shaped pizza where the lengths of the sides are 7 in. Help Abel find the area of the pizza.
The length of the sides $= 7$ in.
Since the sides of the pizza have equal lengths, we can say that it is an equiangular triangle. Hence, using the area formula we get,
Area $= \frac{\sqrt{3}}{4}$ $a^2$
Area $= \frac{\sqrt{3}}{4}$ $(7)^2$
Area $= \frac{\sqrt{3}}{4}$ $49^2$
Area $= 21.21$
Hence, the area of the large pizza eaten by Abel is 21.21 sq. in.
Frequently Asked Questions
What is the formula to find the height of an equiangular triangle?
The formula to find the height of equilateral triangle is:Height, $h = \sqrt{\frac{3a}{2}}$, where a is the side of the equilateral triangle.
Are all equiangular triangles congruent?
An equiangular triangle has three equal angles with congruent sides opposite them making all three sides congruent. Hence, equiangular triangles are congruent.
What is another name of the equiangular triangle?
The other name of an equiangular triangle is an equilateral triangle since both the triangles have similar properties, such as sides are equal and all three angles are measured at $60^\circ$.
What is an orthocenter?
The orthocenter is the point where all the three altitudes of the triangle intersect each other.
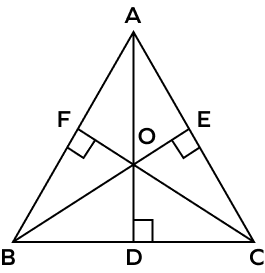
What is a centroid?
The centroid is the point in which the three medians of the triangle intersect is known as the centroid of a triangle.
Do equilateral and equiangular triangles mean the same thing?
Yes! Every equiangular triangle is also equilateral and vice-versa.
What is equiangular quadrilateral?
The quadrilateral in which all the interior angles are congruent is called an equiangular quadrilateral. Example: Square



























