There are many operations in mathematics, such as addition, subtraction, multiplication, and division. They help us evaluate mathematical expressions.

Consider the following expression: 4+ 5 × 32 – 2
The expression consists of many operations. But which part do you calculate first?
You may start from the left and get one answer. But your friend may begin from the right and get a completely different answer!

Note: Both the methods given above are incorrect.
Hence, to avoid confusion, a standard rule was set to perform such calculations. This rule is known as the order of operations.
What Is the Order of Operations in Math?
If you have an expression where all the operations are the same (example: only addition, only subtraction, only multiplication, or only division) then the correct way to solve it would be from left to right. But for expressions with multiple operations, we need to follow the order of operations.
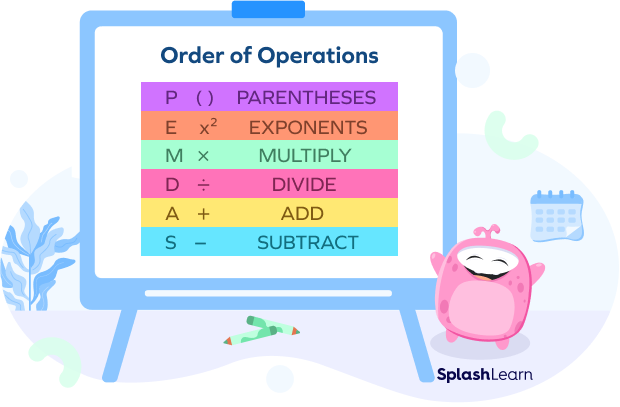
The order of operations is the rule that tells us the sequence in which we should solve an expression with multiple operations.
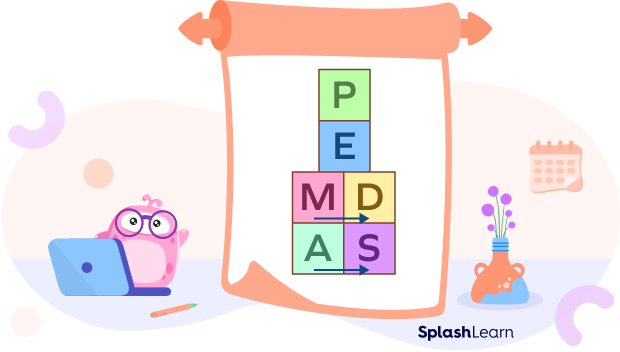
A way to remember that order is PEMDAS. Each letter in PEMDAS stands for a mathematical operation.
Recommended Games
Order of Operations Steps:
Parentheses
The first step is to solve the operation within parentheses or brackets. Parentheses are used to group things together. Work out all groupings from inside to out.
Exponents
Work out the exponential expressions after the parentheses.
Multiplication and Division
Next, moving from left to right, multiply and/or divide, whichever comes first.
Addition and Subtraction
Lastly, moving from left to right, add and/or subtract, whichever comes first.
Recommended Worksheets
Why Follow the Order of Operations?
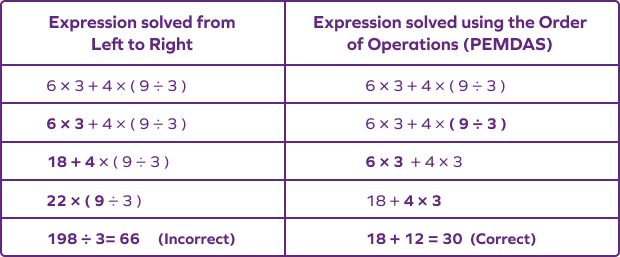
We follow the rules of the order of operations to solve expressions so that everyone arrives at the same answer.
Here’s an example of how we can get different answers if the correct order of operations is NOT followed:
Solved Examples On Order Of Operations
Example 1: Solve: 2 + 6 × (4 + 5) ÷ 3 – 5 using PEMDAS.
Solution:
Step 1 – Parentheses : 2+6 × (4 + 5) ÷ 3 – 5 = 2 + 6 × 9 ÷ 3 – 5
Step 2 – Multiplication: 2 + 6 × 9 ÷ 3 – 5 = 2 + 54 ÷ 3 – 5
Step 3 – Division: 2 + 54 ÷ 3 – 5 = 2 + 18 – 5
Step 4 – Addition: 2 + 18 – 5 = 20 – 5
Step 5 – Subtraction: 20 – 5 = 15
Example 2: Solve 4 – 5 ÷ (8 – 3) × 2 + 5 using PEMDAS.
Solution:
Step 1 – Parentheses: 4 – 5 ÷ (8 – 3) × 2 + 5 = 4 – 5 ÷ 5 × 2 + 5
Step 2 – Division: 4 – 5 ÷ 5 × 2 + 5 = 4 – 1 × 2 + 5
Step 3 – Multiplication: 4 – 1 × 2 + 5 = 4 – 2 + 5
Step 4 – Subtraction: 4 – 2 + 5 = 2 + 5
Step 5 – Addition: 2 + 5 = 7
Example 3: Solve 100 ÷ (6 + 7 × 2) – 5 using PEMDAS.
Solution:
Step 1 – Multiplication inside parentheses: 100 ÷ (6 + 7 × 2) – 5= 100 ÷ (6 + 14) – 5
Step 2 – Addition inside parentheses: 100 ÷ (6 + 14) – 5 = 100 ÷ 20 – 5
Step 3 – Division: 100 ÷ 20 – 5 = 5 – 5 Step 4 – Subtraction: 5 – 5 = 0
Practice Problems On Order Of Operations
Order Of Operations - Definition With Examples
Simplify 4+ (5 ×3² + 2) using PEMDAS.
4 + (5 × 3² + 2)
= 4 + (5 × 9 + 2
) = 4 + (45 + 2)
= 4 + 47
= 51
Simplify 9 – 24 ÷ 8 × 2 + 3 using PEMDAS.
9 – 24 ÷ 8 × 2 + 3
= 9 – 3 × 2 + 3 (Notice that we did division before multiplication because we should go from left to right.)
= 9 – 6 + 3
= 3 + 3 (Notice that we did subtraction before addition because we should go from left to right.)
= 6
Simplify [(32 ÷ 4) + 3] × 2 using PEMDAS.
[(32 ÷ 4) + 3] × 2
= [8 + 3] × 2
= 11 × 2
= 22
Simplify $(3 × 5² ÷ 5)$ – $(16 - 10)$ using PEMDAS.
$(3 × 5² ÷ 5)$ – $(16 – 10)$
= $(3 × 25 ÷ 5)$ – $(16 – 10)$
= $(75 ÷ 5)$ – $(6)$
= 15 – 6
= 9
Frequently Asked Questions On Order Of Operations
What is the order of operations in math?
The order of operations are the rules that tell us the sequence in which we should solve an expression with multiple operations.
The order is PEMDAS: Parentheses, Exponents, Multiplication, and Division (from left to right), Addition and Subtraction (from left to right).
Is there a trick we can use to remember the order of operations?
Yes. You can use the phrase “Please Excuse My Dear Aunt Sally” to remember PEMDAS.
Can we perform subtraction before addition?
Yes, addition and subtraction are at the same level according to the PEMDAS rule. So, without brackets, we do the math from left to right if we are only dealing with addition and subtraction. For example, 9 – 6 + 3 = 3 + 3 = 6.
Can we perform division before multiplication?
Yes, multiplication and division are at the same level according to the PEMDAS rule. So, without brackets, we do the math from left to right if we are only dealing with multiplication and division. For example, 24 ÷ 8 × 2 = 3 × 2 = 6.
Are PEMDAS and BODMAS the same?
Yes. Both PEMDAS and BODMAS are acronyms for remembering the order of operations. They are different names for the same rule. What they call PEMDAS in the US is called BODMAS in the UK, Australia, India and various other countries.
NOTE – Related Readings:




































