What Does “Evaluate Expressions” Mean in Math?
To evaluate simply means finding the value of something. In mathematics, the term “evaluate” refers to finding the numerical value or result of a mathematical expression or equation.
For example, to evaluate the expression “5 + 3” means to perform the addition and find the sum, which is 8.
Evaluating algebraic expressions refers to solving them to determine the specific numeric answer. In order to evaluate an algebraic expression, you need to replace each variable with a numerical value and then carry out the necessary mathematical operations.
In essence, evaluating in math is about calculating and obtaining a numerical value or solution for a given mathematical statement or problem.
Recommended Games
What Is an Algebraic Expression?
Algebraic expressions are mathematical expressions that are made of constants, variables, and algebraic operations.
Recommended Worksheets
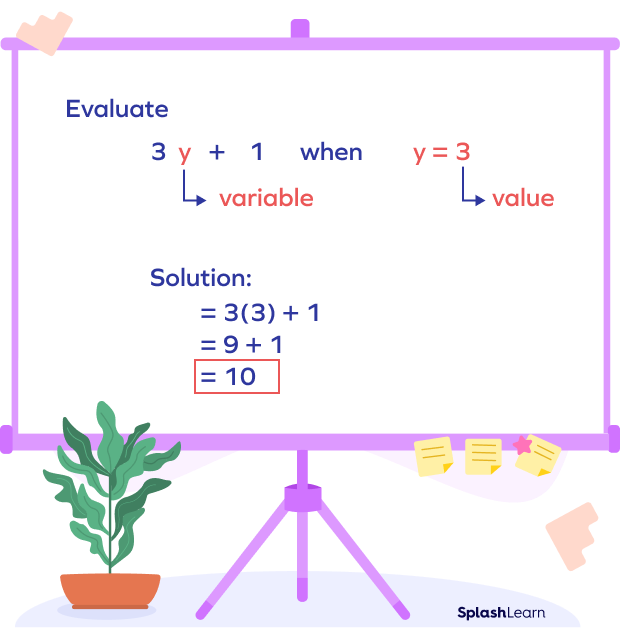
How to Evaluate Expressions in Math
Evaluating an algebraic expression means determining the value of the expression for the given value of each variable in the expression. Replace each variable in the expression with the specified value, and then simplify the resulting expression by specifying the order of operations.
Example 1: Consider an algebraic expression x+5, Let’s evaluate it for x=7.
Substitute the value of x in the expression.
7+5=12.
Example 2: Consider an algebraic expression y2-5y+2. Let’s evaluate it at y=-1.
Substituting y=-1 in the expression, we get
(-1)2-5(-1)+2=1+5+2=8
What Are Terms, Coefficients, Variables, and Constants?
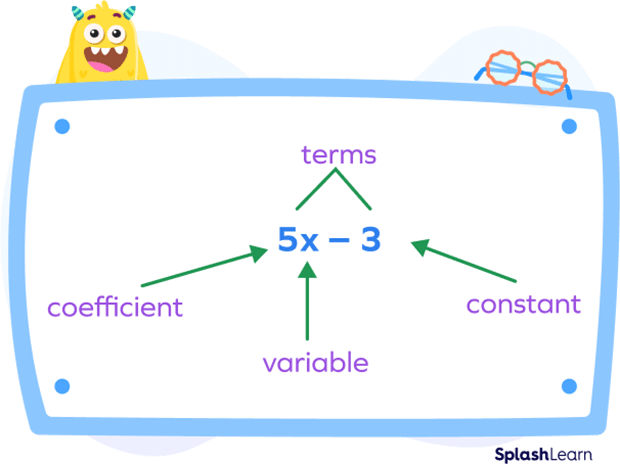
- Terms:
In algebra, an algebraic expression is formed by a term or a group of terms together. Terms are single numbers, variables, or the product of a number and variables.
It can be a single mathematical expression or component that can consist of numbers, variables, or a combination of both, along with any mathematical operations.
Examples of terms: In an algebraic expression x + 2y + 10, there are three terms: x, 2y, and 10.
- Like Terms:
The terms whose variables and their exponent power are the same are called like terms. However, the coefficients of these variables can be different.
These like terms can be combined to simplify the expression to derive the answer.
Example of like terms: 10y and 3y are like terms.
- Variables:
A variable refers to a letter of the alphabet or a symbol used to denote an unknown number, value, or quantity.
- Coefficients:
A coefficient is a number or any symbol representing a constant value that is multiplied by the variable of a single term or the terms of a polynomial. It is usually a number, but sometimes may be replaced by a letter in an expression. In simple words, it is the numerical value that is a multiplier of the variable.
Example: In the expression ax2 + bx + c, x is the variable, ‘a’ is the coefficient of x2, and ‘b’ is the coefficient of x.
In an expression, 5y + 7, the coefficient of y is 5.
How to Simplify Expressions by Combining Like Terms
We can only perform the operations like addition and subtraction when there are two or more like terms.
Example: Consider the expression 4x+2y -5x+6y+8y. Evaluate it for x=2 and y=-1.
If we put x=2 and y=-1 directly in the expression, it will be time-consuming.
Instead, we will first combine the like terms and simplify the expression.
4x+2y -5x+6y+8y
= (4x -5x)+(6y+8y+2y)
=-x+16y
Thus, the simplified expression is -x+16y.
We can easily evaluate it for x=2 and y=-1.
-2+16(-1)=-2-16=-18
Equality, Expressions, and Evaluation
- Equality: It allows us to equate two expressions or values using the equal sign (=).
- Expressions: Expressions are mathematical phrases composed of variables, constants, and operations.
- Evaluation: It is the process of calculating the value of an expression or equation.
Equality is the link that connects expressions and evaluation. It enables us to solve equations, determine variable values, and find the result of mathematical expressions.
How to Translate Word Phrases to Algebraic Expressions
Sometimes we have to write algebraic expressions based on word phrases. The following table will help you understand the translation.
| Operation | Phrase | Expression |
|---|---|---|
Addition | a plus b | a + b |
| the sum of a and b | ||
| a increased by b | ||
| total of a and b | ||
| b added to a | ||
Subtraction | a minus b | a – b |
| difference of a and b | ||
| b subtracted from a | ||
| a decreased by b | ||
Multiplication | a times b | a × b |
| Product of a and b | ||
Division | a divided by b | a $\div$ b |
| the quotient of a and b | ||
| the ratio of a and b | ||
| b by a |
Example: 5 subtracted from the product of 2a and 3b.
- Product of 2a and 3b:
2a × 3b = 6ab
- Subtract 5 from 6ab:
6ab – 5.
Conclusion
In this article, we learned how to evaluate algebraic expressions. We also discussed important concepts associated with evaluating expressions. Let’s solve a few examples and practice MCQs for better comprehension.
Solved Examples on Evaluating Expressions
1. Evaluate the expression 3y – 8 at y = – 4.
Solution:
Substituting y = – 4 in 3y – 8.
3 × (- 4) – 8 = – 12 – 8 = – 20
2. Evaluate the expression 2x2 – 8x – 9 at x = – 1.
Solution:
Substituting x = – 1 in 2x2 – 8x – 9.
2(- 1)2 – 8( – 1)- 9 = 2 + 8- 9 = 1
3. Simplify 3x – 9y + 2x + 4y and evaluate it at x = 0 and y = – 1.
Solution:
3x – 9y + 2x + 4y
Combining the like terms, we get
(3x + 2x) + (- 9y + 4y) = 5x – 5y
Substituting x = 0 and y = – 1
5 × 0 – 5 × (- 1) = 0 + 5 = 5
4. Identify terms, coefficients, variables, and constants.
14a2b – 2ab – 6y2 + 17
Solution:
The terms are 14a2 b,- 2ab,- 6y2 and 17.
Variables are a, b, and y.
Coefficient of a2b is 14.
Coefficient of ab is -2.
Coefficient of y2 is -6.
17 is the constant.
5. Determine the like terms:
-7xy2 + 4xy + 16z3 – 21 + z3 + 8xy + 20x2 y – 8 + 12xy
Solution:
Pairs of like terms are:
- -7xy2 and 20xy2
- 4xy and 8xy
- 16z3 and z3
- -21 and –8
- 8xy and 12xy
6. Convert the following word phrases into algebraic expressions.
ab subtracted from the product of 7x and 8y2.
Solution:
Product of 7x and 8y2 = 7x8y2 = 56 xy2
On subtracting ab from 56xy2, we get 56xy2 – ab.
Practice Problems on Evaluating Expressions
Evaluate Expressions - Definition, Solved Examples, Facts, FAQs
What will be the value of 2x - 9 at x = 0?
Substituting x = 0 in 2x - 9, we get
$2 \times 0 \;-\; 9 = 0 \;-\; 9 = \;-\; 9$
On evaluating the expression xy + 16 + 7x - 6y at x = 1 and y = - 1, we get
Substituting x=1 and y=-1 in xy+16+7x-6y,
$\left[1 \times (-\;1)\right] + 16 + \left[7 \times 1\right] + \left[(-\; 6) \times (-\; 1)\right]$
=- 1 + 16 + 7 + 6
= 28
Simplify: ab - 9xy - 16 ab + 2xy
On combining like terms, we get
(ab - 16ab) + (-9xy + 2xy) = - 15ab - 7xy
In the algebraic expression $-6a^{2}b + 8x\; -\; 7y + 16 \;-\; a^{2}b \;-\; 5xy$, the like terms are:
The like terms have the same variables raised to the same power.
So, the like terms are $-\;6a^{2}b;\;-\;a^{2}b$.
Convert the following word problem into algebraic expression. 12 added to the quotient of x and y and the sum multiplied by 3.
Quotient of x and $y = \frac{x}{y}$.
12 added to $\frac{x}{y}$ gives $\frac{x}{y} + 12$.
3 multiplied to $\frac{x}{y} + 12$ gives $3\left[\frac{x}{y} + 36\right]$.
Frequently Asked Questions about Evaluating Expressions
What is the difference between evaluating expressions and simplifying expressions?
Finding the value of an expression by substitution of values for given variables is known as evaluation. The process of reducing an expression to a simplified form which is easier to work with is known as simplification.
What are unlike terms in an algebraic expression?
Unlike terms are the terms whose variable-part does not match. They either have different variables with same power, or same variables with different power, or different variables with different power.
What is the difference between algebraic expression and equation?
An algebraic expression is either a constant, a variable, or a combination of constants and variables involving algebraic operations. On the other hand, an algebraic equation is made up of two algebraic expressions connected by an equal sign.
Why is it important to use the order of operations to evaluate algebraic expressions?
Addition, subtraction, multiplication, and division are the mathematical operations. The order of operations is important because it guarantees that people can all read and solve a problem in the way.
Why is the simplification of an expression important?
Simplification of expressions is a handy mathematics skill because it gives us a chance to change complex or awkward expressions into simpler forms.
























