Definition of Equilateral Triangle
In geometry, an equilateral triangle is a triangle whose all three sides are of equal length. The sides of an equilateral triangle are congruent, which means that all sides are of equal length. All the interior angles are equal(60 degrees) too.
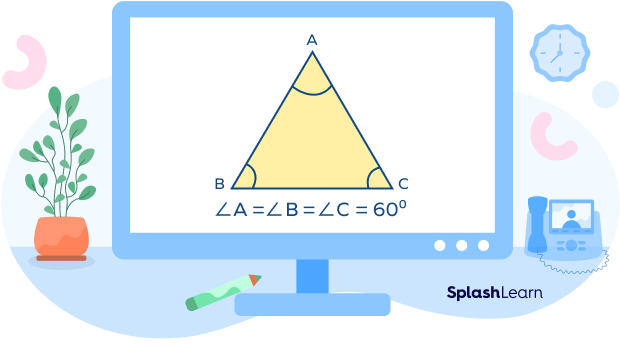
The term equilateral is made up of ‘equi,’ which means equal, and ‘lateral,’ which means side. So, a triangle with equal sides is known as an equilateral triangle.
Recommended Games
History of Equilateral Triangles
The traces of triangles can be found all over the world, especially in construction. The ancient Egyptians were fond of them. The faces of the famous Pyramids of Egypt are triangular. The pyramids of Giza are the most famous pyramids built by the Egyptians in the second century B.C. Egyptians thought that the triangular shape of the pyramid symbolized the seat of their Sun God, Ra, on earth.
Recommended Worksheets
Equilateral Triangles used in Real Life
- The traffic sign boards we see on the road are in the shape of equilateral triangles. Next time you go out for a car ride, notice that all the three sides of a signboard seem to be of equal length.

- The racks used to set a pool table with pool balls are equilateral triangles. They fit a total of 15 balls, creating a perfect equilateral triangle.
- Nachos, a common snack, are also triangular. Some of them are indeed equilateral.

What are NOT Equilateral Triangles?
- The face of a traffic cone is not an equilateral triangle because all three sides are not equal. A traffic cone has elongated sides with a smaller base.
- Sails on a sailing boat are not equilateral triangles since the sides are not equal in length. Two of the sides are longer than the remaining side.
Properties of Equilateral Triangles
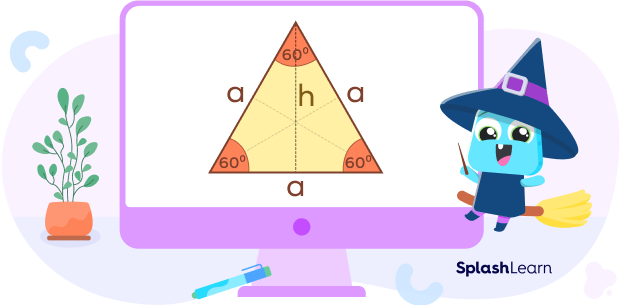
- All sides are of the same length ‘a’
- All interior angles are equal to 60 degrees.
- An equilateral triangle is symmetrical, which means if you fold it to join its vertices, it will fold with the two halves perfectly overlapping each other.
Perimeter and Area of Equilateral Triangle
- You can calculate the perimeter (length of the whole boundary) of an equilateral triangle by adding the lengths of all three sides. In an equilateral triangle of side length ‘a’, the lengths of the sides are equal. So perimeter of equilateral triangle = a + a + a = 3.a
- The area of an equilateral triangle can be calculated using the formula, Area = $\frac{\sqrt{3}}{4})\times a^2$; where a is the side of an equilateral triangle.
Fun Facts about an equilateral triangle
- The faces of the Pyramids of Giza in Egypt are one of the world’s oldest and largest examples of equilateral triangles. They were built in the 26th century B.C. and are perfectly equilateral.
- An equilateral triangle is a special isosceles triangle having all the three sides equal.
Solved Examples
Q1. What will be the perimeter of an equilateral triangle, assuming that all its sides are 30 inches in length?
Solution:
You know that the perimeter of an equilateral triangle is 3 times the side length. It is given in the question that side length = 30 inches.
Therefore, the perimeter of an equilateral triangle will be 3 × 30 = 90 inches.
Q2. What will be the perimeter and semi perimeter of an equilateral triangle whose side measurement is 10 units?
Solution:
You know the perimeter of an equilateral triangle is 3 times the side length, and the semi-perimeter is half the perimeter.
Put in the values: side length = 10 units.
Therefore, the perimeter of the equilateral triangle will be 3 × 10 = 30 units and
the semi-perimeter of an equilateral triangle will be $\frac{30}{2}$ = 15 units.
Q3. What will be the area of the equilateral triangle PQR if PQ = QR = RP = 2 cm?
Solution:
Apply the formula, area = $\frac{\sqrt{3}}{4}\times side^2$
As per the question, side length = 2 cm
Therefore,
Area = $\frac{\sqrt{3}}{4}\times side^2 = \frac{\sqrt{3}}{4}\times 2^2 = \sqrt{3} cm$
Practice Problems
Equilateral Triangles
What is the area of an equilateral triangle whose side measures 10 cm?
$\frac{\sqrt{3}}{4}\times10^{2}$ = $\frac{\sqrt{3}}{4}\times10\times10$ = $\sqrt{3} \times5\times5$ = 25 $\sqrt{3}cm^{2}$
What is the area of an equilateral triangle whose perimeter is 12 cm?
Area of the equilateral triangle = $\frac{\sqrt{3}}{4}\times \frac{12}{3}\times \frac{12}{3}$ = $\frac{\sqrt{3}}{4}\times 4\times 4$ = $4\sqrt{3} cm^{2}$
Find the area of an equilateral triangle if the sides lengths measure 20 inches.
Area of Equilateral Triangle = $\frac{\sqrt{3}}{4}\times side^{2}$ = $\frac{\sqrt{3}}{4} \times 20^{2}$ = $100\sqrt{3}$ square inches
Frequently Asked Questions
What do we mean by equilateral?
The term equilateral is made up of ‘equi,’ which means equal, and ‘lateral,’ which means side. So if a shape has all the sides of the same length it is called equilateral.
What are the properties of an equilateral triangle?
The three properties of an equilateral triangle are:
- All three sides are equal.
- All three angles are congruent.
- The figure has three lines of symmetry.
How do you know if a triangle is equilateral?
You can know that a triangle is equilateral by measuring its sides. If they are of equal lengths, then the triangle is equilateral.
Can a right triangle be equilateral?
An equilateral triangle can never be a right angled as a right-angled triangle has one of the angles as 90° whereas an equilateral triangle has all angles equal to 60°
Is an equilateral triangle isosceles?
An equilateral triangle is a special case of an isosceles triangle having not just two, but all three sides and angles equal.



























