Triangle
A triangle is a three-sided closed figure. It is one of the basic shapes in geometry which has 3 sides and 3 vertices. The triangle can be classified as equilateral, isoscles or scalene on the basis of the length of it’s sides.
Recommended Games
What is the Perimeter of a Triangle?
The perimeter of a polygon is the total length of the boundary. For a triangle, we can find it by adding the lengths of its three sides.
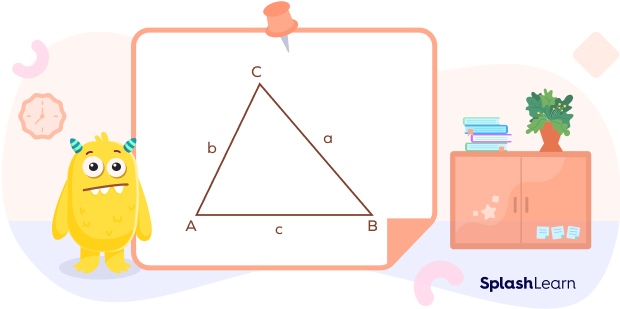
So, if ABC is a triangle. We find the perimeter of triangle ABC by adding the length of all three sides.
Perimeter of △ABC = AB + BC + CA = a + b + c
Let’s understand this by using a real-life example.
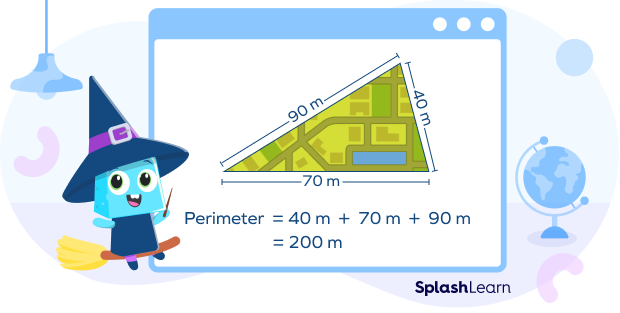
Suppose we have a triangular park. We need to find the length of the fence required to cover the park. How do we find that?
We can find the length of the fencing required for a triangular park by finding the perimeter of the triangle.
Let’s take another example.
A serving tray as shown forms an equilateral triangle – that is, a triangle with three equal sides. Let each side be 20 cm long.
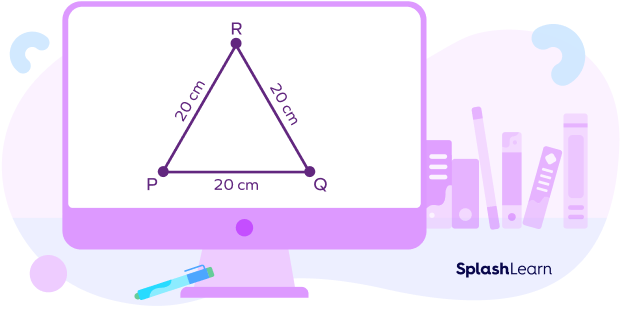
To find the total length of a decorative lace to be pasted on outside borders, one needs to find the perimeter of the triangle. Since all the three sides of the triangle are of equal length, we can find the perimeter by multiplying the length of each side by 3.
20 + 20 + 20 = 3 × 20 = 60 cm.
Thus, we can see that the perimeter of an equilateral triangle is 3 times the length of each side.
Recommended Worksheets
What is the Area of a Triangle?
The area of a two-dimensional shape is the space occupied by the shape. This area can be found by dividing the shape into unit squares and determining the number of unit squares in the shape as each unit square occupies one square unit space.
Consider a rectangle with length of 4 cm and width of 3 cm. It can be filled with 3 rows and 4 columns of unit squares and therefore the area is 3 times 4 or 12 square centimeters. That is, the area of a rectangle is the product of its length and width.
A rectangle can be divided into two congruent triangles.
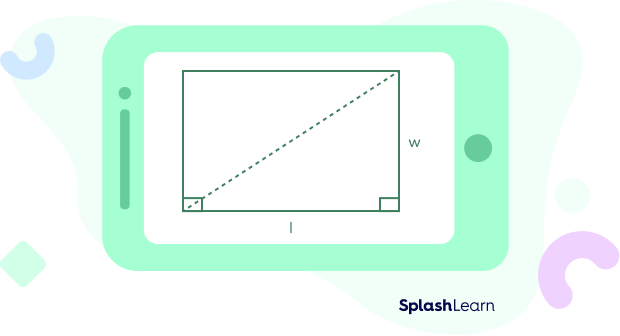
So, the area of each triangle is half the area of the rectangle. That is 12 × l × w, where l stands for length of the rectangle and w stands for width of the rectangle.
Consider a scalene triangle △ABC. Note that, to write the area of a triangle as half the area of a rectangle, we need to have the height perpendicular to the base. So, draw a perpendicular from a vertex to the opposite side.
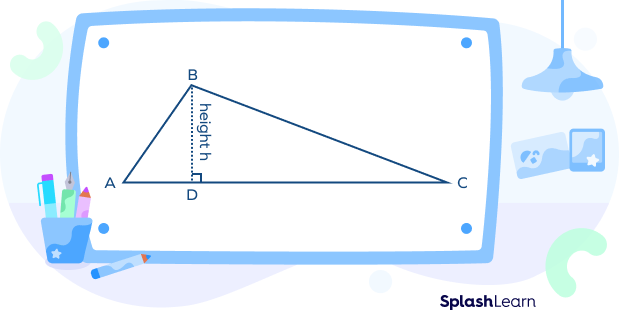
Here, BD is the perpendicular drawn from vertex B to the opposite side AC.
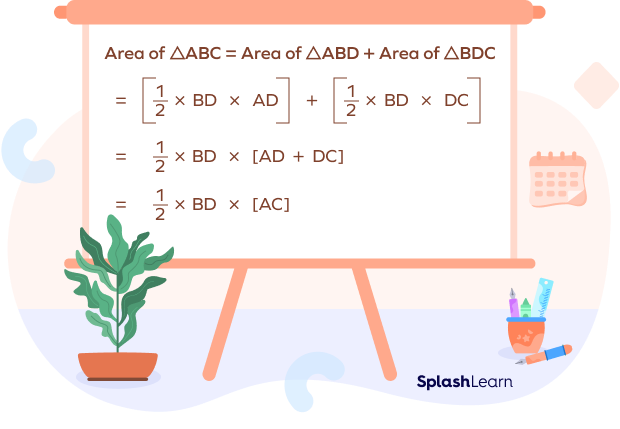
Thus, the area of a triangle is half the product of its base and height.
Area of a triangle = ½ × base × height.
Fun Facts
- A triangle is the simplest polygon with three sides. All other polygons have more than three sides.
- The word perimeter is taken from Greek words meaning “around measure.”
- The area A of an equilateral triangle of side length s cm can be calculated using the formula A=34× s2. The value of 3 is about 1.73. Thus, the approximate becomes, A = 0.4325 s2.
Solved Examples on Area and Perimeter of Triangle
- The sides of a triangle have the following lengths:
10 cm, 14 cm, and 12 cm
Find the perimeter of the triangle.
Solution. We know that the perimeter of a triangle is the sum of all its sides. Hence,
perimeter = 10 cm + 14 cm + 12 cm = 36 cm.
- An equilateral triangle has one side of length 6 cm. Find the perimeter of the triangle.
Solution. As all sides of an equilateral triangle are equal in length, its perimeter can be calculated as shown:
Perimeter = 6 cm + 6 cm + 6 cm = 18 cm
- The perimeter of a triangle is 25 cm. Two of its sides measure 4 cm and 10 cm. Find the length of the third side.
Solution. Perimeter is the sum of all sides. We can find the third side by subtracting the measures of the other two sides from the given perimeter.
Length of the third side = 25 cm – (4 cm + 10 cm) = 11 cm
- The height of a triangle is 4 cm, and its base is 5 cm. Find its area.
Solution. We know that the area of a triangle is given by 12 x base x height. Hence,
Area = 12 × 4 × 5 = 10 cm sq.
Practice Problems on Area and Perimeter of Triangle
Area and Perimeter Of A Triangle
What is the perimeter of a triangle with sides lengths 3 cm, 6 cm, and 4 cm?
Perimeter = 3 cm + 6 cm + 4 cm = 13 cm
The side of an equilateral triangle is 3 cm in length. Find the perimeter of the triangle.
Perimeter = 3 cm + 3 cm + 3 cm = 9 cm
The perimeter of a triangle is 15 cm. The lengths of the two sides are 5 cm and 4 cm. Find the length of the third side.
Length of the third side = 15 cm – 5 cm – 4 cm = 6 cm
The sides of a triangle are 4 cm, 4 cm, and 3 cm. Find the perimeter.
4 cm + 4 cm + 3 cm = 11 cm.
The base of a triangle is 8 cm. Its height is 6 cm. What is the area?
Area = $\frac{1}{2}\times 8\times 6$ = 24 cm sq.
Frequently Asked Questions on Area and Perimeter of Triangle
What is the formula for the perimeter of a triangle?
The formula for the perimeter of a triangle is the sum of the length of all the sides of a triangle. For example, if the side lengths of a triangle are 3 cm, 4 cm, and 5 cm, then the perimeter of the triangle will be 3 + 4 + 5 = 12 cm.
Does area increase as perimeter increases?
An increase in perimeter of a figure always increases the area of the figure.
What is the perimeter of an isosceles triangle?
The perimeter of an isosceles triangle is 2 x side + base.
How do we define the area of a triangle?
The area of a triangle is space occupied within it’s boundary. It can be calculated as half the product of its base and height.
What is the similarity between the perimeter and area?
Both area and perimeter define the size of a shape.




































