What Is the Perimeter of a Triangle?
The perimeter of a triangle is the sum of all its sides. In other words, the perimeter of a triangle is the total length of its boundary.
A triangle is a polygon, a closed, 2-dimensional shape with three sides, three angles, and three vertices. Its perimeter is calculated by adding the length of all the sides. A perimeter of a 2D shape is measured in linear units of measurement like inches, feet, yards, etc.
Recommended Games
Perimeter of a Triangle: Definition
The perimeter of a triangle can be defined as the sum of all sides of a triangle.
A triangle has three sides.
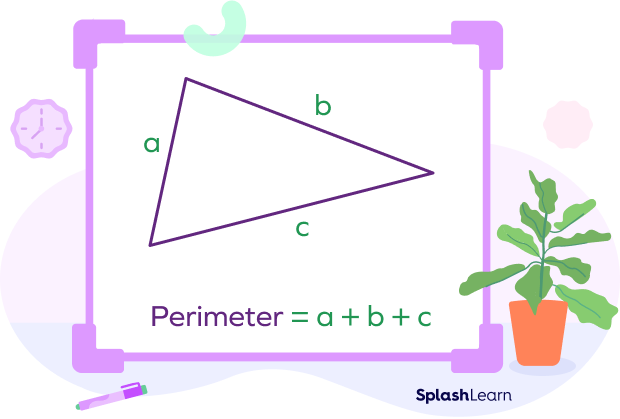
Perimeter of a Triangle $=$ Sum of three sides of the triangle
Recommended Worksheets
Perimeter of a Triangle Formula
What is the formula for the perimeter of a triangle? Let’s find out.
Let a, b, and c be the lengths of the three sides of a triangle.
Perimeter of triangle $= a + b + c$
How to Find the Perimeter of a Triangle
Step 1: Note down the lengths of all three sides of the given triangle. Ensure that the lengths are in the same unit.
Step 2: Add the lengths of the three sides.
Step 3: The sum represents the perimeter of the given triangle. Assign the same unit to the perimeter as the length of the sides.
Perimeter of an Equilateral Triangle
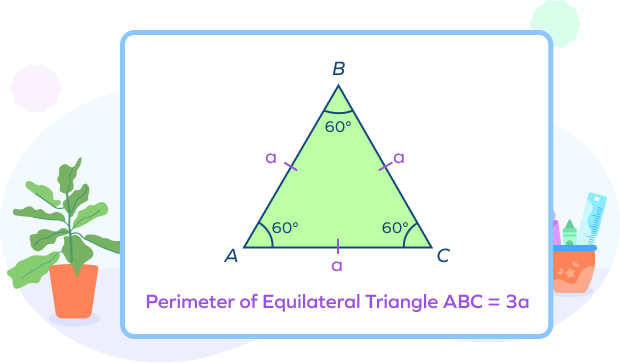
A triangle with three equal sides and three congruent angles $(60^\circ)$ is known as an equilateral triangle.
Consider an equilateral triangle ABC whose each side measures “a” units.
Perimeter of an equilateral triangle $= a + a + a = 3a$
So, how do you find the perimeter of a triangle with three equal sides? Simply multiply the length of the side by 3!
Perimeter of an Isosceles Triangle
A triangle with two equal sides is known as an isosceles triangle.
Since two sides of a triangle are equal, we have $a = b$
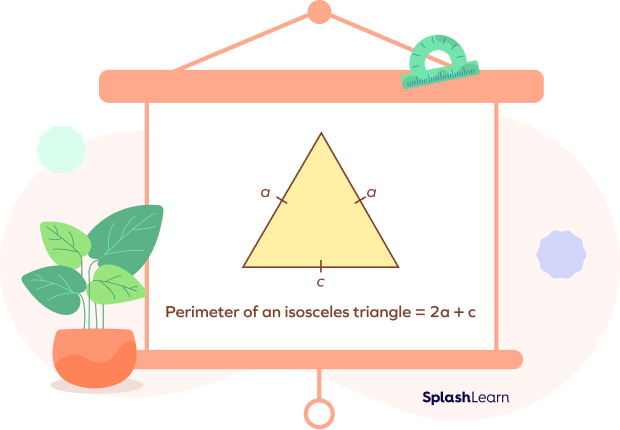
Perimeter of an isosceles triangle $= a + a + c = 2a + c$
Perimeter of a Scalene Triangle
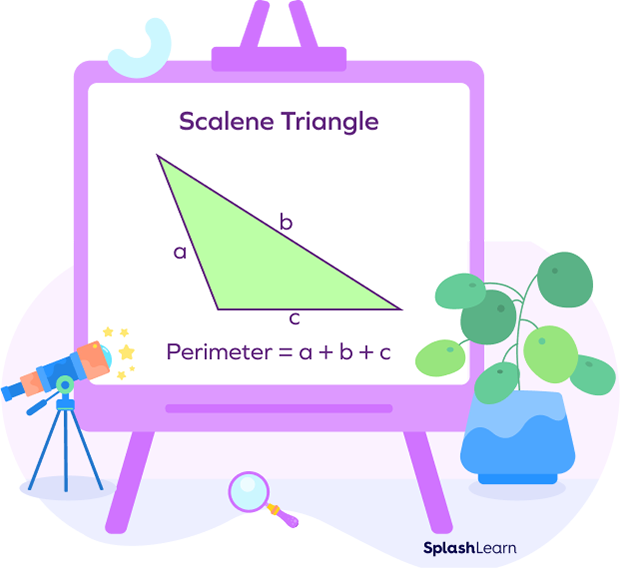
A triangle in which all the sides have different lengths is known as a scalene triangle.
If the lengths of three sides are given by a, b, and c, then
Perimeter $= a + b + c$
Perimeter of a Right-angled Triangle
A triangle in which one interior angle is $90^\circ$ is called a right triangle. The side opposite to the $90^\circ$ angle is called a hypotenuse. The other two sides are termed as “legs” of the right triangle. A right triangle has a base (b), hypotenuse (h), and perpendicular (p) as its sides.
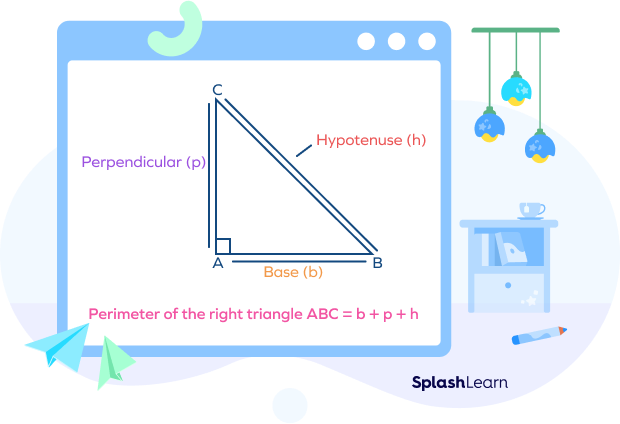
Going by Pythagoras’ theorem, we know that
$h^2 = p^2 + b^2$
Therefore, the perimeter of a right angle triangle $= b + p + h$
$= b + p + \sqrt{p^2 + b^2}$
Perimeter of an Isosceles Right Triangle
A right triangle in which the base and the height (two legs) are of equal length is called an isosceles right triangle.
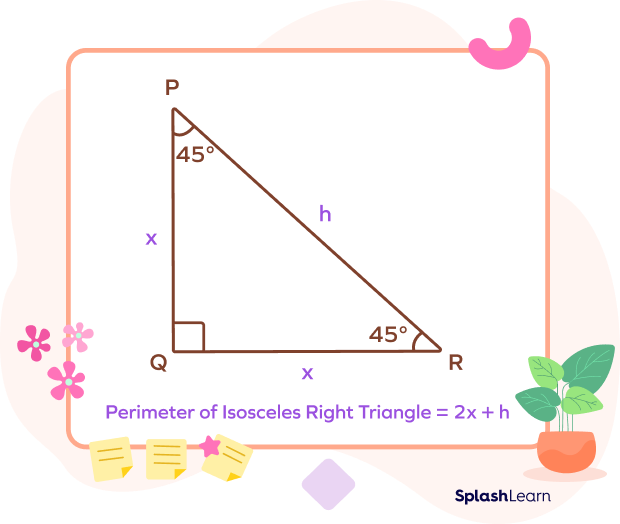
Applications of Perimeter of a Triangle
Take a look at the triangular park. Supposing we have to fence it along the outer boundary, we need to find the length of the fence required to cover the park. How do we do that? The length of the fence required can be calculated by finding the total length of the boundary (perimeter) of the triangle.

Solved Examples on Perimeter of a Triangle
1. Find the perimeter of an equilateral triangle with side 6 inches.
Solution:
Side of an equilateral triangle $= a = 6$ inches
Perimeter of an equilateral triangle $= 3a$
$=3 \times 6$
$= 18$ inches
2. What is the perimeter of an isosceles triangle whose equal sides are 4 feet each and the unequal side is 6 feet?
Solution:
Let equal sides be $a = 4$ feet and non equal side be $b = 6$ feet
Perimeter of the given isosceles triangle $= 2a+b$
$=(2 \times 4)+ 6$
$= 14$ feet
3. If the perimeter of the given triangle is 34 feet, what is the length of the missing side?
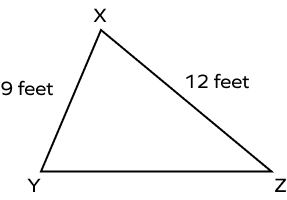
Solution:
In the $\Delta XYZ$, we have
$XY = 9$ feet
$XZ = 12$ feet
Perimeter $= 34$ feet …given
Perimeter of the triangle $= XY + YZ + XZ$
$34 = 9 + 12 + YZ$
$34 = YZ + 21$
$YZ = 13$ feet
4. What is the value of x if the perimeter of the triangle PQR is 40 units? Also, find the length of three sides.

Solution:
Perimeter of triangle $PQR = PQ + QR + PR$
$40 = x + x + 4 + x + 6$
$40 = 3x + 10$
$3x = 30$
$x = 10$
Let’s find the length of the sides.
$PQ = x = 10$ units
$QR = x + 6 = 10 + 6 = 16$ units
$PR = x + 4 = 10 + 4 = 14$ units
5. If the base and height of a right isosceles triangle is 6 inches each, what would be its perimeter?
Solution: $b = p = 6$ inches
$h^2 = p^2 + b^2$
$h = \sqrt{p^2 + b^2} = \sqrt{6^2 + 6^2} = \sqrt{36+36} = \sqrt{72} = 6\sqrt{2}$ inches
Perimeter of a right triangle$ = b + p + h = 6 + 6 + 6\sqrt{2} = (12 + 6\sqrt{2})$ inches
Practice Problems on Perimeter of a Triangle
Perimeter of a Triangle – Definition, Formula, Examples, FAQs
What is the perimeter of $\Delta ABC$?

Perimeter of an isosceles triangle $= 3 + 3 + 4 = 6 + 4 = 10$ inches
The perimeter of an equilateral triangle is 45 inches. What is the side of the triangle?
Let the side of an equilateral triangle be a inches
Perimeter of an equilateral triangle = 3a = 45 inches
$3a = 45$
$a = \frac{45}{3} = 15$ inches
If the perimeter of a scalene triangle is 32 feet. If the two sides are 12 feet and 7 feet, then what is the third side?
Let $a = 12$ feet, $b = 7$ feet and $c = ?$ feet
Perimeter of the triangle $= a + b + c$
$32 = 12 + 7 + c$
$c = 32\;-\;12\;-\;7 = 32\;-\;19 = 13$ feet
Find the perimeter of a right angled isosceles triangle whose two sides are 4 inches each.
$b = p = 4$ inches
$h^2 = p^2 + b^2$
$h = \sqrt{p^2 + b^2} = \sqrt{4^2 + 4^2} = \sqrt{16 + 16} = \sqrt{32} = 4\sqrt{2}$ inches
Perimeter of a right triangle $= b + p + h = 4 + 4 + 4\sqrt{2} = (8 + 4\sqrt{2})$ inches
Frequently Asked Questions on Perimeter of a Triangle
What is the difference between area and perimeter?
Area is the region bounded within the sides of a 2D shape, whereas perimeter is the total length of the boundary of the shape.
What is the formula for the area of a triangle?
Area of a Triangle $= \frac{1}{2} \times base \times height$
What is the semiperimeter of a triangle?
Semiperimeter is the half of the perimeter of a triangle. If the sides of a triangle are a,b and c, then the semiperimeter $= \frac{a + b + c}{2}$




























