What Is an Isosceles Right Triangle?
An isosceles right triangle is a right-angled triangle whose base and height (legs) are equal in length. It is a type of special isosceles triangle where one interior angle is a right angle and the remaining two angles are thus congruent since the angles opposite to the equal sides are equal.
It is also known by the name of right-angled isosceles triangle or a right isosceles triangle.
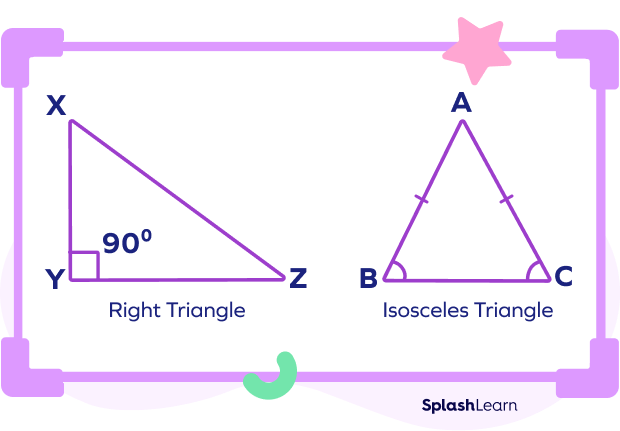
When you combine these two properties together, you get an isosceles right triangle.
Isosceles Right Triangle: Definition
An isosceles right triangle is a type of right triangle whose legs (base and height) are equal in length.
Since the two sides of the right triangle are equal in measure, the corresponding angles are also equal. Therefore, in an isosceles right triangle, two sides and the two acute angles are equal.
Thus, the interior angles of an isosceles right triangle are $90^{\circ},\; 45^{\circ},\;45^{\circ}$.

Recommended Games
Isosceles Right Triangle Hypotenuse
The hypotenuse of a right angled triangle is the longest side of the triangle, which is opposite to the right angle.
It is equal to exactly $√2$ times the length of the congruent sides of the triangle. If the length of each of the equal sides is x units, then the length of the hypotenuse of the isosceles right triangle will be equal to $\sqrt{2x}$ units.
This property is derived using the Pythagoras’ theorem. Here’s a right triangle, $\Delta PQR$:

Recommended Worksheets
How to Find the Hypotenuse of an Isosceles Triangle
To find the hypotenuse of an isosceles right triangle, we use the Pythagorean theorem.
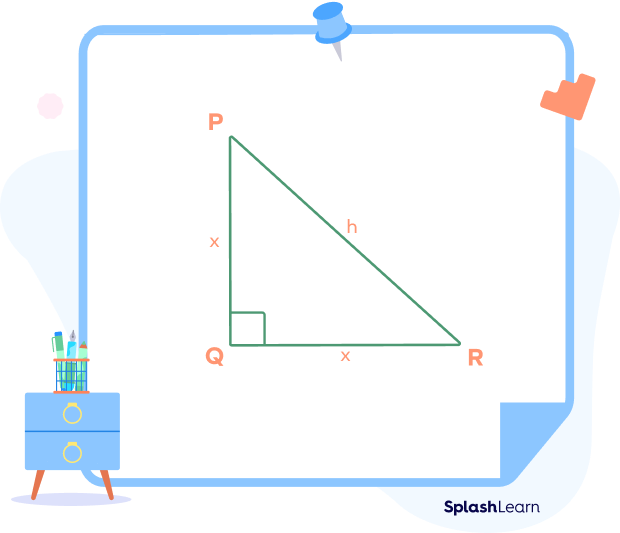
We know that in an isosceles right triangle, two sides are of equal length.
Now, if we assume both the sides to be equal to x units, the hypotenuse can be calculated as:
$Hypotenuse^{2} = x^{2} + x^{2}$ _______________(By Pythagoras’ theorem)
$Hypotenuse^{2} = 2x^{2}$
$Hypotenuse= \sqrt{2x^{2}}$
$Hypotenuse= \sqrt{2}x$
We can use the above derived result as it is without applying the Pythagoras’ theorem every time. The length of the hypotenuse of an isosceles right triangle will always be equal to $√2$ times the length of the equal sides of the triangle.
Isosceles Right Triangle Formulas
We just discussed the formula to find the hypotenuse of an isosceles right triangle. It is given by
Hypotenuse $= \sqrt{2} \times$ Length of congruent sides
Now let’s discuss the formulas to find the perimeter and area of the right angled isosceles triangle.
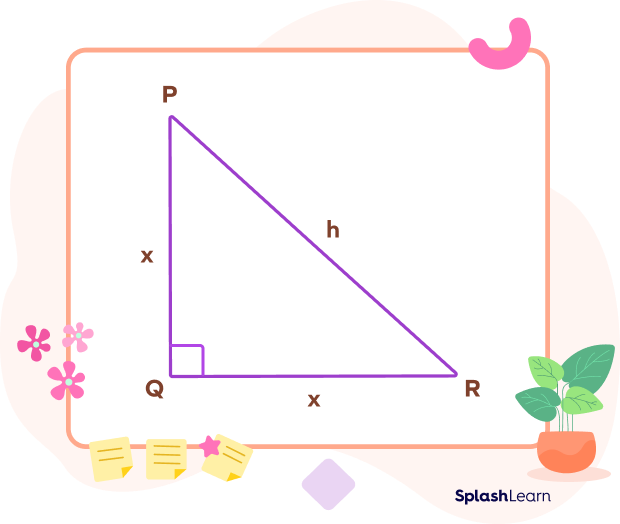
Area of an Isosceles Right Triangle
Area of a triangle $= \frac{1}{2} \times$ Base $\times$ Height.
In $\Delta PQR ,\; PQ = QR = x$, where PQ is the height and QR is the base.
The area of the isosceles right triangle $= \frac{1}{2} \times PQ \times QR$
$= \frac{x \times x}{2}$
$= \frac{x^{2}}{2}$ sq. units.
Therefore, the area of the isosceles right triangle formula is $\frac{x^{2}}{2}$, where “x” is equal to the congruent side length.
Perimeter of an Isosceles Right Triangle
Perimeter of a triangle $=$ Sum of lengths of all its sides
Perimeter of isosceles right triangle $\Delta PQR = PQ + QR + PR$
$PQ = QR = x$ units
$PR = h$ units
Perimeter of the isosceles right triangle formula $= x + x + h = (2x + h)$ units.
Therefore, the perimeter of the isosceles right triangle formula is $2x + h$, where “x” represents the length of congruent sides and “h” is equal to the length of the hypotenuse.
Isosceles Right Triangle Properties
- It has one interior angle, which is equal to $90^{\circ}$.
- The sides or legs are perpendicular to each other and are also known as the base and the height. They are congruent.
- The other two angles of an isosceles right triangle are acute angles and are congruent to each other. They are equal to $45^{\circ}$ each.
- The sum of all the interior angles measures $180^{\circ}$.
- If we draw an altitude from the right angle vertex to the hypotenuse (the opposite side), then it is the perpendicular bisector of the hypotenuse.
- The area of an isosceles right triangle is equal to $12 \times$ Base $\times$ Height square units.
Fun Facts!
- Since the two sides of an isosceles right triangle are equal, the angles are also equal. And both the angles measure 45 degrees.
- Right angle is always the largest angle in a right triangle.
- There can’t be any obtuse angles in a right triangle.
Conclusion
In this article, we explored the properties of the isosceles right triangle. Let’s solve some practice problems for better understanding.
Solved Examples on Isosceles Right
1. The equal sides of an isosceles right triangle are 5 units each. Calculate the length of its hypotenuse.
Solution:
We know that the formula to calculate the hypotenuse of an isosceles right triangle is:
Hypotenuse $= \sqrt{2\; x}$
where, “x” is the length of the congruent side.
The equal sides measure 5 units.
Therefore, the hypotenuse will be equal to $\sqrt{2 \times 5} = 7.071$ units.
2. The length of the base of an isosceles right triangle is 10 units. What will be the area of this triangle?
Solution:
We know that the formula to calculate the area of an isosceles right triangle is:
$\frac{x^{2}}{2}$ square units, where x is the measure of the congruent side of the triangle.
Area $= \frac{10^{2}}{2} = \frac{100}{2} = 50$ square units.
3. The area of an isosceles right triangle is 72 square units. What is the measure of its base?
Solution:
We know that the formula to calculate the area of an isosceles right triangle is:
$\frac{x^{2}}{2}$ square units, where x is the measure of the congruent side of the triangle.
Given that the area of the triangle is 72 square units.
Putting this value in the formula:
$\frac{x^{2}}{2} = 72$
$x^{2} = 72 \times 2 = 144$
$x = \sqrt{144}$
$x = 12$ units.
Therefore, the measure of the base of an isosceles right triangle with area equal to 72 square units is 12 units.
4. The height of a right isosceles triangle is 8 units. What will be its perimeter?
Solution:
The perimeter of an isosceles right triangle $= (2x + h)$ units.
x is equal to the length of the congruent side
h is the measure of the hypotenuse.
The height of this isosceles right triangle is 8 units.
Here,
$Hypotenuse = \sqrt{2x}$
$h = \sqrt{2 \times 8} = 11.3137$ units
$Perimeter = 2x + h = (2 \times 8) + 11.3137 = 27.3137$ units.
5. The perimeter of an isosceles right triangle is equal to $10 + 5\sqrt{2}$ units. If the non-congruent side is equal to $5\sqrt{2}$ units then, find the measure of the congruent sides.
Solution:
We know that the formula to calculate the perimeter of an isosceles right triangle is: $(2x + h)$ units.
Where, x is equal to the length of the congruent side and h is the measure of the hypotenuse.
$Perimeter = 10 + 5\sqrt{2}$ units
Hypotenuse $= 5\sqrt{2}$ units
Putting this in the above formula:
$10 + 5\sqrt{2} = 2x + 5\sqrt{2}$
$10 = 2x$
$x = 5$ units.
Therefore, the congruent side is equal to 5 units.
Practice Problems on Isosceles Right Triangle
Isosceles Right Triangle: Definition with Examples
The equal sides of an isosceles right triangle are 7 units each. What is the length of its hypotenuse?
Hypotenuse $= \sqrt{2x}$
where, x is the length of the congruent side.
Given that, the equal sides measure 7 units.
Therefore, the hypotenuse will be equal to $\sqrt{2 \times 7} = 9.8994 \approx 10$ units.
The length of the base of an isosceles right triangle is 10 units. What will be the area of this triangle?
Area of an isosceles right triangle $= \frac{x^{2}}{2}$ square units, where x is the length of the congruent sides of the triangle.
Here, $x = 10$ units. Area $= \frac{10^{2}}{2} = \frac{100}{2} = 50$ square units.
The area of an isosceles right triangle is 32 square units. What is the measure of its base?
Area of an isosceles right triangle = x22 square units, where x is the length of the congruent sides of the triangle.
$\frac{x^{2}}{2} = 32$
$x^{2} = 32 \times 2 = 64$
$x = \sqrt{64}$
$x = 8\;$ units
Therefore, the measure of the base of an isosceles right triangle with area equal to 32 square units is 8 units.
The area of the isosceles right triangle whose base and height equal 1 unit is ____________.
Area of isosceles right triangle $= \frac{x^{2}}{2} = \frac{1}{2}$ sq. units
The hypotenuse of the isosceles right triangle whose equal sides are given by x units is
The hypotenuse of the isosceles right triangle is given by $\sqrt{2x}$, where x represents the length of the congruent sides.
Frequently Asked Questions on Isosceles Right Triangle
Are all isosceles right triangles $45^{\circ}\;-\;45^{\circ}\;-\;90^{\circ}$?
Yes, all the isosceles right triangles have interior angles measuring $45^{\circ},\; 45^{\circ},\;$ and $90^{\circ}$. This is because one angle has to be a right angle (90 degree), and consequently, the other two angles have to be equal as the opposite sides are equal.
What are the types of triangles based on length of sides?
- Isosceles triangle: Two sides are congruent.
- Equilateral triangle: All sides are congruent.
- Scalene triangle: All sides are of different lengths.
What is an acute angled triangle?
A triangle that has all angles measuring less than 90 degrees is called an acute-angled triangle.
What is an obtuse angled triangle?
A triangle that has one of its angles going beyond 90 degrees, is called an obtuse-angled triangle.
What are three types of isosceles triangles?
Isosceles triangles can be classified into three types: 1) acute isosceles triangle, 2) obtuse isosceles triangle, and 3) right isosceles triangles.




























