What Is an Isosceles Triangle?
A triangle with two sides of equal length is an isosceles triangle.
Examples of Isosceles Triangle:
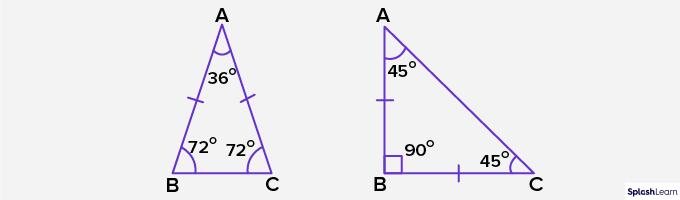
Non-example of Isosceles Triangle:
Examples of Isosceles Triangles in Real Life:
Many things in the world have the shape of an isosceles triangle. Some popular examples of these triangles in real life are:
Recommended Games
Parts of an Isosceles Triangle
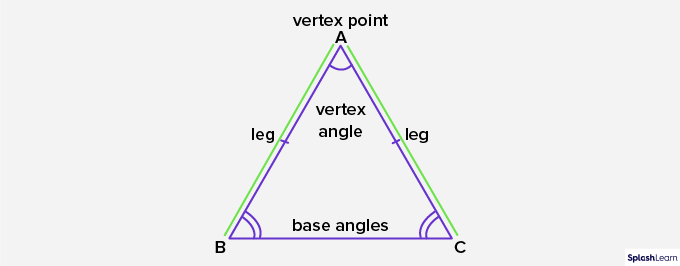
Source: Parts of an isosceles triangle
1. Legs: The two equal sides of an isosceles triangle are called “legs.” In triangle ABC, sides AB and BC are the two legs of the isosceles triangle.
2. Base: The ‘base’ of an isosceles triangle is the third and unequal side. Here, side BC is the base of the isosceles triangle ABC.
3. Vertex angle: The vertex angle is formed by two equal sides of an isosceles triangle. ∠BAC is the vertex angle of the isosceles triangle.
4. Base angles: The ‘base angles’ are the angles that involve the base of an isosceles triangle. ∠ABC and ∠ACB are the two base angles of the isosceles triangle.
Properties of an Isosceles Triangle
Here is a list of some properties of isosceles triangles:
- In an isosceles triangle, if two sides are equal, then the angles opposite to the two sides correspond to each other and are also always equal.
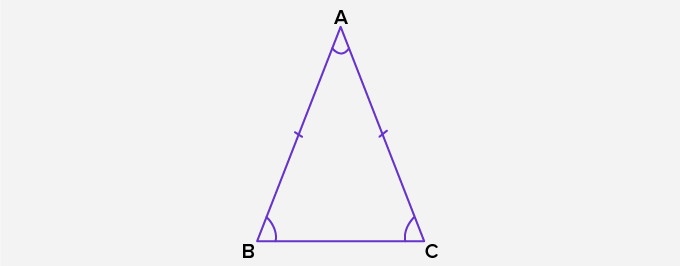
In the given isosceles triangle ABC, the two angles ∠B and ∠C, opposite to the equal sides AB and BC, are equal to each other.
- The sum of three angles of an isosceles triangle is always 180°.
Types of Isosceles Triangles
Generally, isosceles triangles are classified into three different types:
- Isosceles acute triangle: An isosceles acute triangle is a triangle in which all three angles are less than 90 degrees, and at least two of its angles are equal in measurement. One example of isosceles acute triangle angles is 50°, 50°, and 80°.
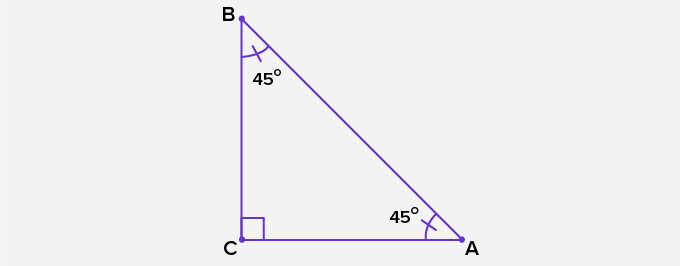
- Isosceles right triangle: This is a right triangle with two legs (and their corresponding angles) of equal measure.
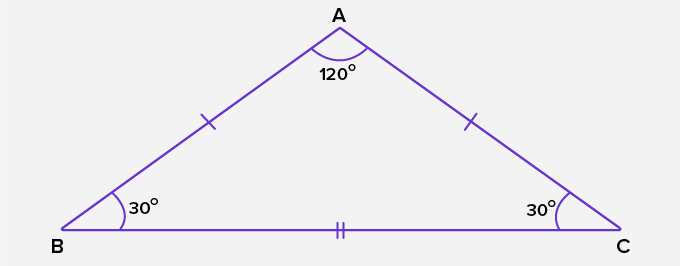
- Isosceles obtuse triangle: An isosceles obtuse triangle is a triangle in which one of the three angles is obtuse (lies between 90 degrees and 180 degrees), and the other two acute angles are equal in measurement. One example of isosceles obtuse triangle angles is 30°, 30°, and 120°.
Recommended Worksheets
Isosceles Triangle Formulas
- Area of an Isosceles Triangle: The area of an isosceles triangle is given by the following formula:
Area = $\frac{1}{2}$ × base × height
A = $\frac{1}{2}$ × b × H
- Perimeter of an Isosceles Triangle: The perimeter of the isosceles triangle is given by
Perimeter = Sum of equal sides + base
Perimeter = 2a + b
Here, ‘a’ refers to the length of the equal sides of the isosceles triangle, and ‘b’ refers to the length of the third unequal side.
Solved Examples on Isosceles Triangle
Example 1: What is the height of an isosceles triangle with an area of 12 sq. cm and a base of 6 cm?
Solution:
Area of isosceles triangle = ½ × base × height
12 = ½ × 6 × height
12 = 3 × height
Height = 4 cm
Example 2: How do you calculate the perimeter of an isosceles triangle with two sides of length ‘a’ cm each and a third side of length ‘b’ cm?
Solution:
Perimeter of an isosceles triangle = sum of its sides
Perimeter of an isosceles triangle = (a + a + b) cm
Perimeter = (2a + b) cm
Example 3: Find the perimeter of an isosceles triangle if the base is 16 cm and the equal sides are 24 cm each.
Solution:
The formula of the perimeter of an isosceles triangle is
P = 2a + b
Here, a (length of equal sides) = 24 cm and b (base) = 16 cm
Therefore, the perimeter of an isosceles triangle = P= 2(24) + 16 = 64 cm
Hence, the perimeter is 64 cm.
Practice Problems on Isosceles Triangles
Isosceles Triangles
What is the height of an isosceles triangle with an area of 10 sq. cm and a base of 5 cm?
Area of an isosceles triangle = $\frac{1}{2}$ × base × height
10 cm2 = 12 × 5 cm × height
Height = 4 cm
In ΔABC, if ∠A = ∠B, then
Given: ∠A = ∠B
Sides opposite to equal angles are also equal.
In ΔABC, side BC is opposite to ∠A, and side AC is opposite to angle B.
Therefore, AC = BC.
What is the area of the given isosceles triangle?
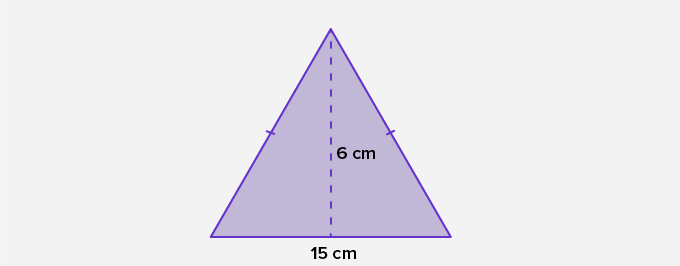
Area of an isosceles triangle = $\frac{1}{2}$ × base × height = $\frac{1}{2}$ × 15 cm × 6 cm = 45 cm2
Frequently Asked Questions about Isosceles Triangle
How do we know if a triangle is isosceles?
A triangle is said to be an isosceles triangle if any of its two sides are equal. Let’s take a triangle that has AB, BC, and CA as its three sides. If any of these are true—AB = BC, BC = CA or CA = AB—then the triangle is isosceles.
Can a right triangle also be an isosceles triangle?
Yes, a right triangle or right-angle triangle can be an isosceles triangle. An isosceles right triangle will have 1 right angle and 2 other angles as equal angles.
Can you find all the angles of an isosceles triangle if you know one of the equal angles?
Yes! We know that the sum of all angles of a triangle is equal to 180 degrees. If we know the two equal angles, we can easily add them and subtract the sum from 180 degrees to find the third angle.
What are some of the properties of an isosceles triangle?
- It has two sides of equal length.
- The angles opposite to the equal sides are also equal in measure.



























