Sides of Equal Length

Sides of Equal Length – Introduction

Mathematics is not just about numbers, it also includes the study of different shapes like circles, squares, ovals, cylinders, triangles, rectangles, and many more.

It involves finding the measurement of sides or the accurate angles of the shapes. 

Today, we will discuss shapes that have sides of equal length. We will learn the factors that make them different from each other and their respective names. Let’s get started!

What Are Sides of Equal Length?

Sides of equal length mean that they measure the same. In simple words, the sides of a shape that have the same length are the sides of equal length.

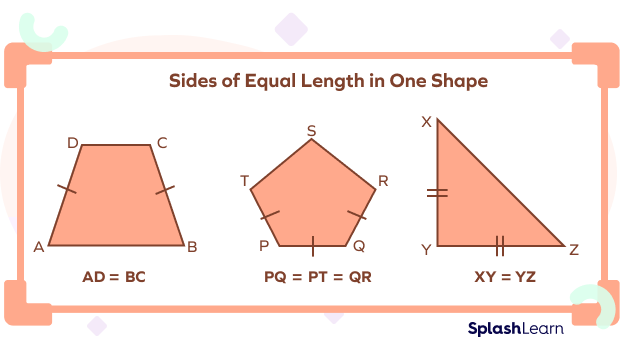
Sides that are equal in length are also known as congruent sides. These sides could be part of one single shape or different shapes. Let’s see some examples of figures with sides of equal lengths. 

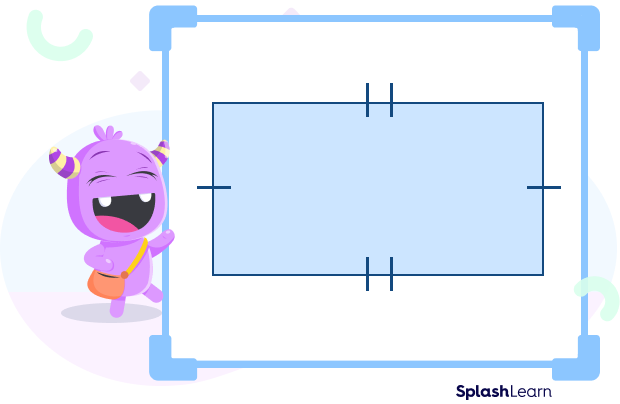
In the rectangle below, the opposite sides are congruent to each other. 

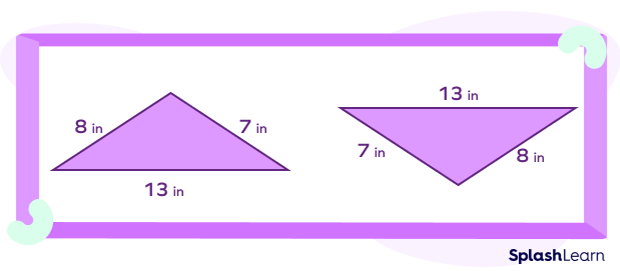
In the two triangles below, the sides are congruent to each other. 

Sides of Equal Length in One Shape

Triangles 

Based on the length of the sides, triangles can be categorized as scalene, isosceles, and equilateral triangles.

• Scalene triangle:

It is a triangle in which each side is of a different length.

• Isosceles triangle:

It is a triangle in which two sides are of equal length. The angle falling between the equal sides is known as the vertex angle. The angles opposite to the two equal sides of a triangle will always be equal. Similarly, if two angles of a triangle are equal, then their corresponding opposite sides will also be of equal length.

• Equilateral triangle:

It is a triangle in which all three sides are of equal length. Each angle of an equilateral triangle measures 60°. Hence, it is also termed an equiangular triangle.

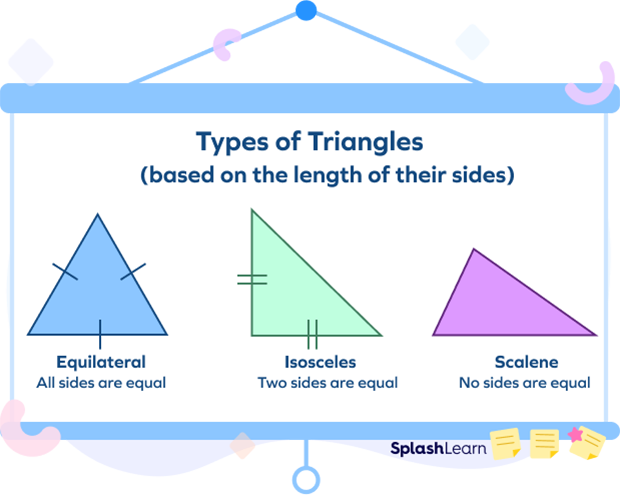
So, triangles with equal sides could either be isosceles or equilateral.

Quadrilaterals 

Quadrilaterals are polygons with four sides. They can also have all or some of their sides equal. Different categorizations are listed below:

1. All sides equal 

In these quadrilaterals, all four sides are equal. They are also known as regular quadrilaterals. Examples of regular quadrilaterals are a square and a rhombus. 

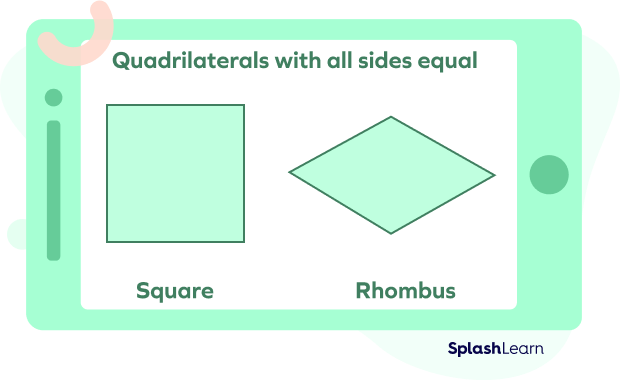
2. Three equal sides 

In these quadrilaterals, three sides are equal. 

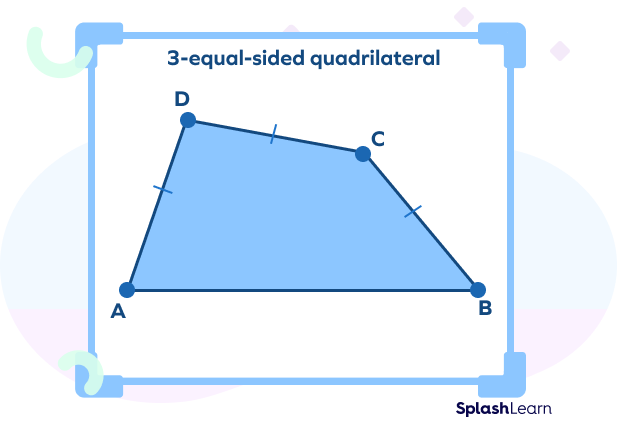
3. One pair of equal sides 

In these quadrilaterals, there is one pair of equal sides. The sides may be either opposite or adjacent to each other.

1. Opposite sides are equal: an example of this is an isosceles trapezium

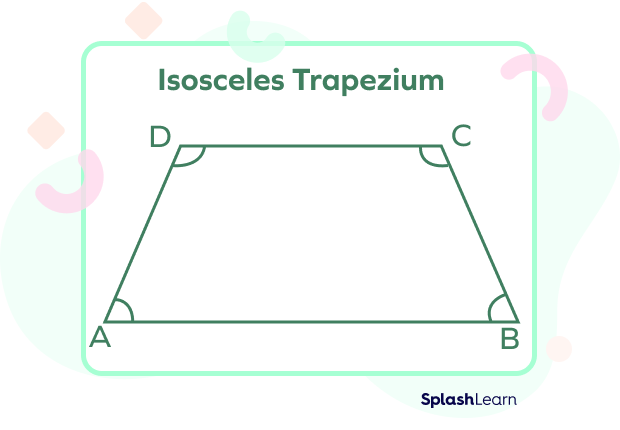
2. Adjacent sides are equal: an example of this is an irregular quadrilateral with two adjacent sides equal. 

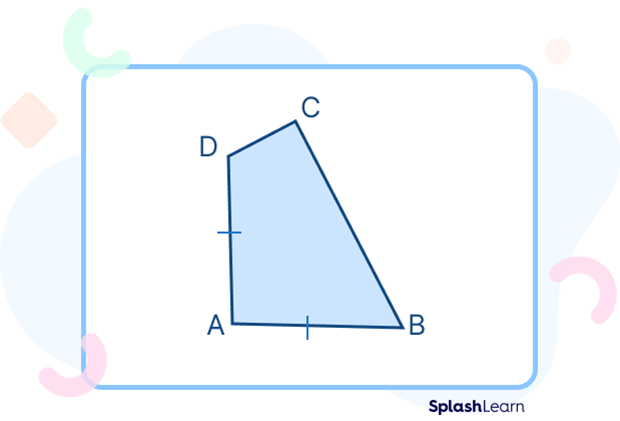
4. Two pairs of equal sides 
5. Equal sides are opposite: Examples are a rectangle and a parallelogram. 

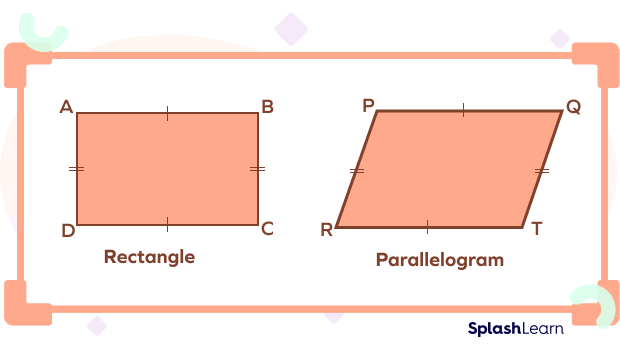
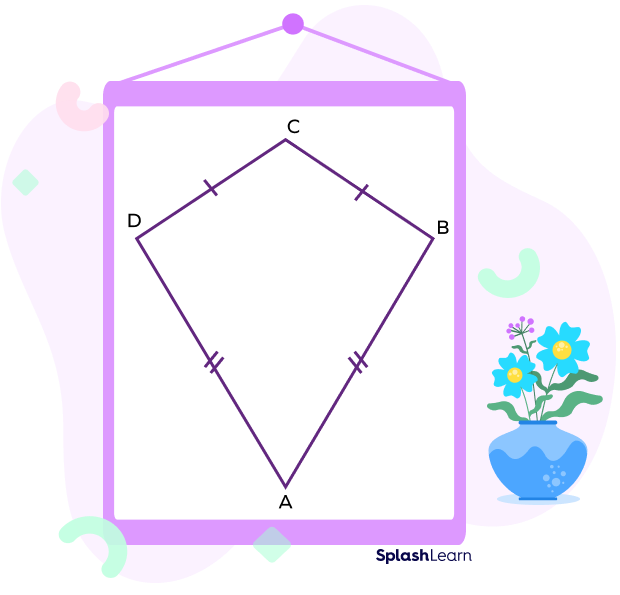
2. Equal sides are adjacent: An example is a kite.

Polygons 

Polygons are two-dimensional closed figures consisting of only straight sides. Polygons can have any number of sides. This means triangles and quadrilaterals are also polygons. Polygons can also have all or some of their sides equal. 

1. Regular Polygons: 

Polygons with all sides and all interior angles equal are known as regular polygons. All their angles are also equal. Note that instead of having all equal sides, a rhombus is not a regular polygon because all its interior angles are not equal.

2. Irregular Polygons: 

Polygons with all sides not equal are known as regular polygons. They may have some sides of equal length but not all. So, even if rectangles and parallelograms have opposite sides equal, they are irregular polygons.

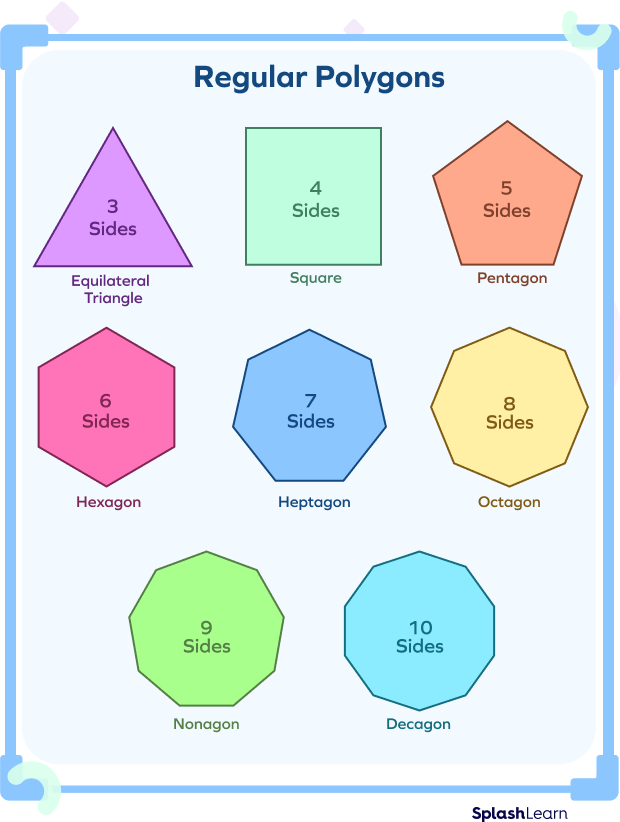
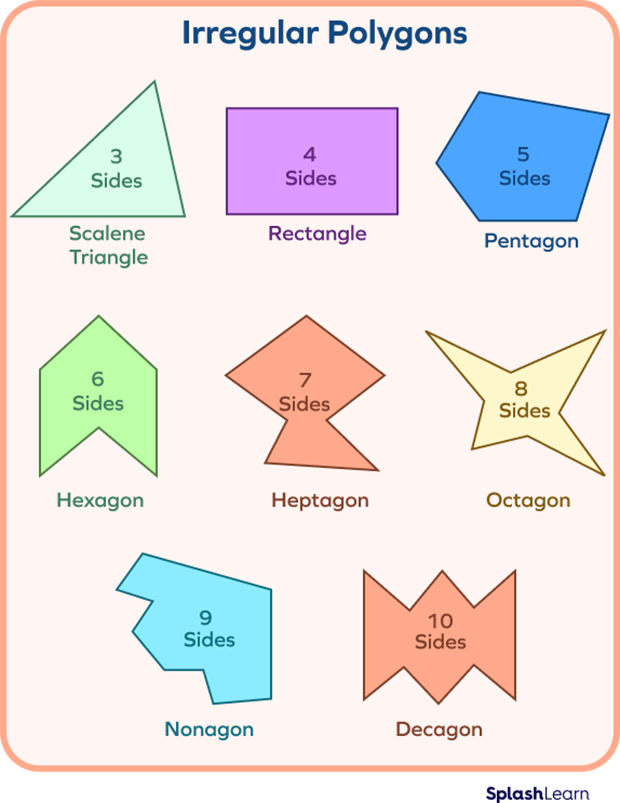
Sides of Equal Length in Different Shapes

When comparing different shapes, if a side of one shape is equal to the side of another, the sides are said to be congruent.

If all the sides of one shape are equal to all the sides in the other shape and the angles are also the same, the two shapes are said to be congruent.

For example, two triangles are said to be congruent if all their corresponding sides and angles are equal. 

Criteria for Congruence in Triangles

We need not measure all the sides and angles of two triangles to check if they are congruent or not. If they follow any one of the given criteria, then they are congruent. 

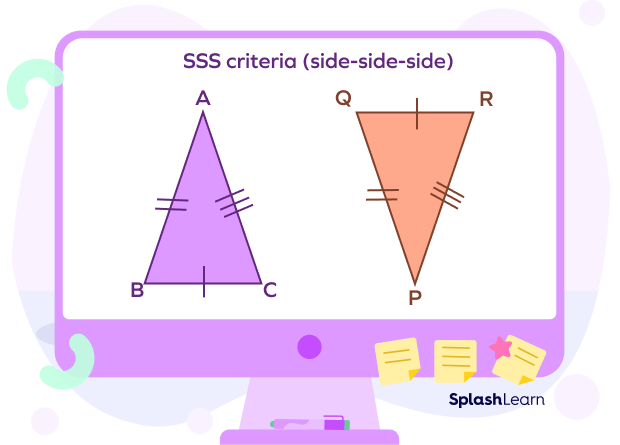
1. SSS criteria (side-side-side)

Two triangles $\Delta\text{ABC}$ and $\Delta\text{PQR}$ are said to be congruent by SSS criteria if their corresponding sides are equal. 

• AB $=$ PQ
• BC $=$ QR
• AC $=$ PR

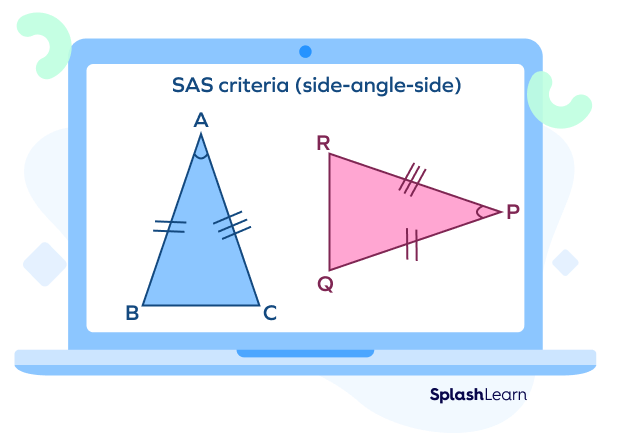
2. SAS criteria (side-angle-side)

Two triangles $\Delta{ABC}$ and $\Delta{PQR}$ are said to be congruent by SAS criteria if two of their corresponding sides and the angle between them are equal. 

• AB $=$ PQ
• ∠A $=$ ∠P
• AC $=$ PR

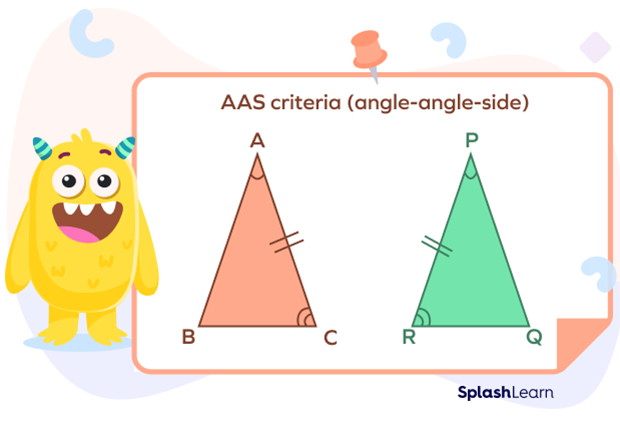
3. AAS criteria (angle-angle-side)

Two triangles $\Delta\text{ABC}$ and $\Delta\text{PQR}$ are said to be congruent by AAS criteria if any two of their corresponding angles and any one side are equal. 

• ∠A $=$ ∠P
• ∠C $=$ ∠R
• AC $=$ PR

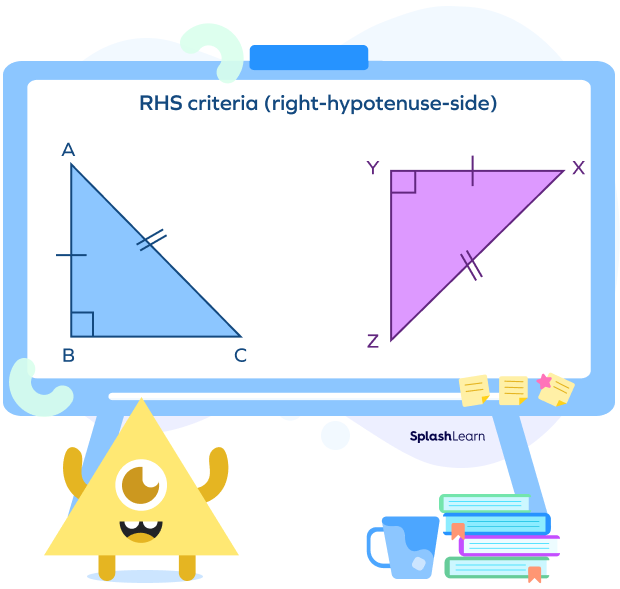
4. RHS criteria (right-hypotenuse-side)

Two right triangles $\Delta\text{ABC}$ and $\Delta\text{XYZ}$ are said to be congruent by RHS criteria if their corresponding hypotenuse and one pair of corresponding sides are equal. 

• ∠B $=$ ∠Y (right angle)
• AC $=$ XZ (hypotenuse)
• AB $=$ XY (side)

Conclusion

In some shapes, all sides are equal, while in others, none of the sides is equal. Also, there are shapes that have only some equal sides. We can compare the sides and angles of different shapes to find congruent sides and congruent shapes. 

Solved Examples 

1. Name three shapes that have all sides of equal length.

Solution: Three shapes that have all sides of equal length are a rhombus, a square, and an equilateral triangle.

2. Find the perimeter of a regular hexagon if one of its sides equals 9 inches. 

Solution: A regular hexagon has 6 sides of equal length.

Since the side equals 9 inches, the perimeter will be: 

$6 \times 9 = 54$ inches. 

3. If two sides of a triangle are equal, what kind of triangle is it? 

Solution: It is an isosceles triangle. An isosceles triangle has two equal sides.  

4. If one side of a parallelogram is 10 inches and the other side is 6 inches, what is the total perimeter? 

Solution: In a parallelogram, the opposite sides are equal to each other.

If one side is 10 inches and the other side is 6 inches, the total perimeter will be:

$10 + 10 + 6 + 6 = 32$ inches.

Practice Problems

Frequently Asked Questions