What Is the Perimeter of a Polygon?
The total distance of the boundary of a polygon is known as the perimeter of a polygon. It is the sum of all the sides of a polygon.
Meaning of Perimeter
In geometry, the perimeter of any 2D shape or figure is defined as the total length of its boundary. The perimeter of a 2D shape is calculated by adding the length of all the sides or the edges enclosing the shape. It is measured in linear units of measurement like inches, feet, meters, centimeters, etc.
Polygon
In geometry, a polygon can be defined as a plane flat, two-dimensional closed shape which is bounded with straight sides. If any side is curved, it is not a polygon. The points where two sides meet are the vertices (or corners) of a polygon.
Examples of a polygon:
There are two types of polygons.
- Regular Polygons: A polygon that has equal sides as well as equal interior angles is known as a regular polygon. Examples: equilateral triangle, square.
- Irregular Polygons: A polygon that is neither equilateral nor equiangular is known as an irregular polygon. Examples: rectangle, scalene triangle.
Recommended Games
Perimeter of a Polygon Formula
Perimeter of a polygon is the total length of all sides of a polygon. .
Perimeter of a Polygon $=$ Sum of all sides
So, how can we find the perimeter of a polygon? First ensure that all the side-lengths have the same unit. If the lengths of sides are given in different units, then first convert them to the same unit. Finally, add lengths of all sides to find the perimeter.
Let’s look at an example to understand.
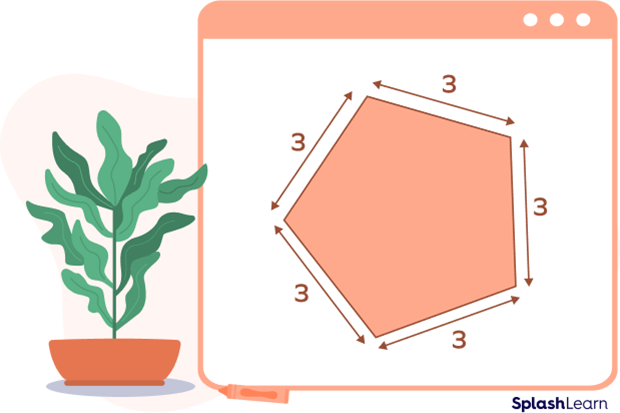
Example: In the given regular pentagon, the length of each side is 3 units. Its perimeter is calculated by adding the length of all sides.
Perimeter $= 3 + 3 + 3 + 3 + 3 = 15$ units
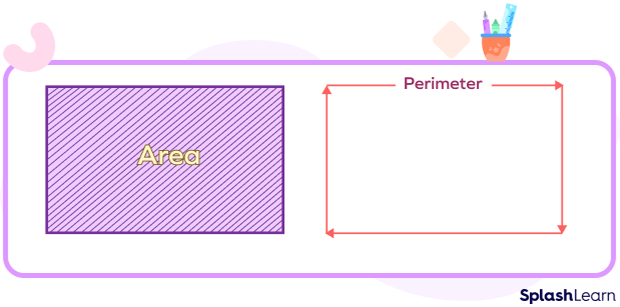
Difference between Area and Perimeter of a Polygon
| Area of a Polygon | Perimeter of a Polygon |
|---|---|
| Area of a polygon is the region bounded within the sides of the polygon. | Perimeter of a polygon is the total length of its boundary. |
| Formula for the area of a polygon is different for different polygons.Examples:Area of a square $= (Side)^{2}$Area of a rectangle $= $length $\times$ width | We can give the generalized formula to find the perimeter of a polygon as: Perimeter of a polygon $=$ Sum of all sides |
| The area of polygons is expressed in square units like $in^{2},\; ft^{2},\; m^{2},\; cm^{2}$, etc. | The perimeter is expressed in linear units like in, ft, m, cm, etc. |
The diagram illustrates the difference between the area and perimeter of a rectangle.
Perimeter of Regular Polygons
In regular polygons, the length of each side is the same. To find the perimeter, we simply multiply the side-length by the number of sides.
Perimeter of regular polygon $=$ (number of sides of regular polygon) $×$ (length of one side)
Example 1: Find the perimeter of a regular hexagon whose each side is 7 feet long.
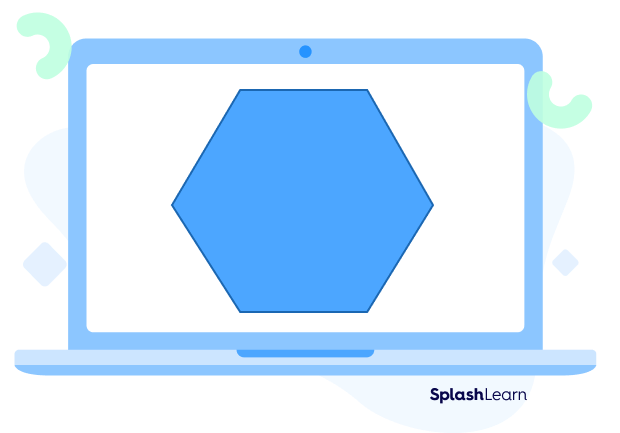
Solution:
Length of one side $= 7$ feet
Number of sides $= 6$ (as it is a hexagon).
Perimeter $=$ (number of sides) $\times$ (length of one side)
Perimeter $= 6 \times (7\; feet)$
Perimeter $= 42$ feet
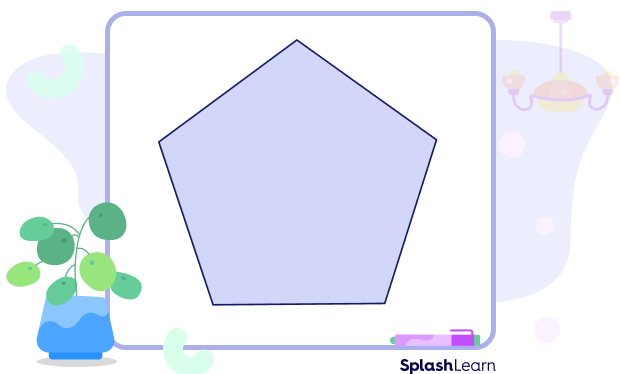
Example 2: Each side of a pentagon equals to 6 inches. Find the perimeter of the pentagon.
Solution:
All the sides of the pentagon are equal. Therefore, it is a regular polygon.
The perimeter of a regular polygon $=$ (length of one side) $\times$ number of sides
Perimeter of a regular pentagon $= 6\; cm \times 5 = 30$ cm
Perimeter Formulas of Some Common Regular Polygons
| Regular Polygons | Perimeter of Regular Polygon |
|---|---|
| Equilateral Triangle | $3 \times$ (Length of one side) |
| Square | $4 \times$ (Length of one side) |
| Regular Pentagon | $5 \times$ (Length of one side) |
| Regular Hexagon | $6 \times$ (Length of one side) |
Perimeter of Irregular Polygons
To calculate the perimeter of irregular polygons, we just add the lengths of all sides of the polygon.
Example 1: Find the perimeter of the given polygon.
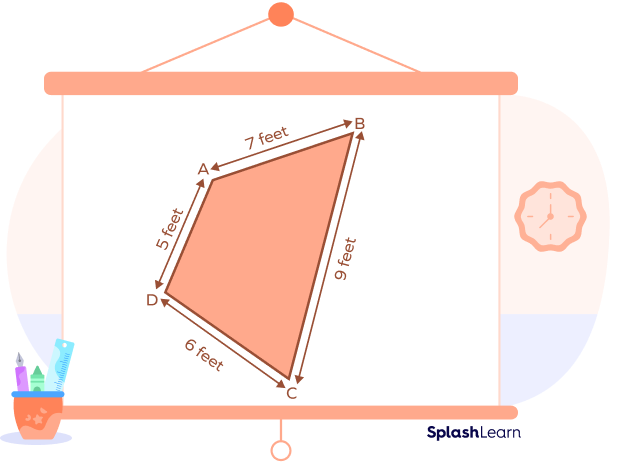
Solution: As we can see that the given polygon is an irregular polygon since the length of each side is different.
$AB = 7$ feet, $BC = 9$ feet, $CD = 6$ feet, and $AD = 5$ feet
The perimeter of $ABCD = AB + BC + CD + AD$
$\Rightarrow$ Perimeter of $ABCD = (7 + 9 + 6 + 5) = 27$ feet
Perimeter Formulas of Common Irregular Polygons
Let’s discuss some important formulas.
Perimeter of a Rectangle
Perimeter of a rectangle $= 2 \times (l + b)$
Perimeter of a rectangle $= 2l + 2b$
where l is the length and b is the breadth
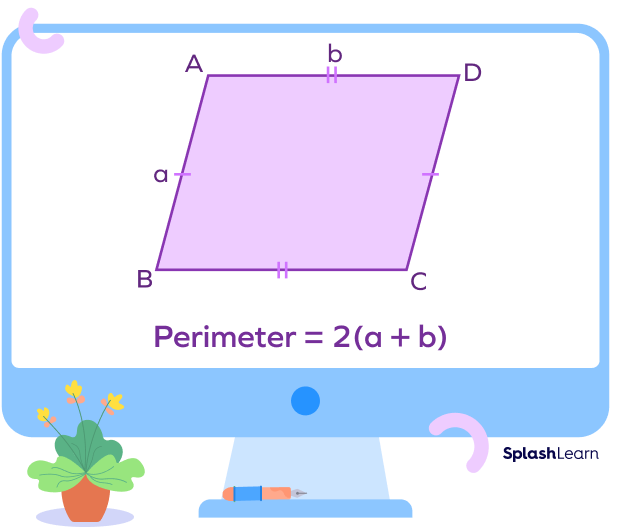
Perimeter of a Parallelogram
Perimeter of a parallelogram $= 2 \times$ (sum of parallel sides)
Perimeter of a parallelogram $= 2(a + b)$

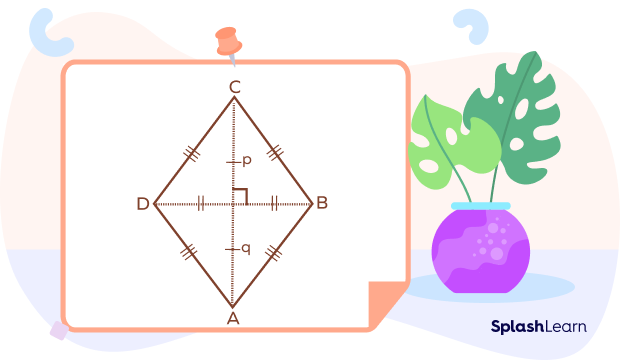
Perimeter of a Rhombus
All four sides of a rhombus have the same length.
Perimeter of Rhombus $= 4 \times$ (length of one side)
Perimeter of Polygon Using Coordinates of Vertices
The perimeter of a polygon can be found if the coordinates of the vertices are given using the following steps:
Suppose we have to find the perimeter of the polygon ABCD with coordinates A(0, 0), B(0, 4), C(4, 4), and D(4, 0).
Step 1: Find the lengths of sides using distance formula.
$D = \sqrt{(x_{2}\;-\;x_{1})^{2} + (y_{2}\;-\;y_{1})^{2}}$
Here,
$AB = \sqrt{(0\;-\;0)^{2} + (4\;-\;0)^{2}} = \sqrt{16} = 4$ units
$BC = \sqrt{(4\;-\;0)^{2} + (4\;-\;4)^{2}} = \sqrt{16} = 4$ units
$CD = \sqrt{(4\;-\;4)^{2} + (0\;-\;4)^{2}} = \sqrt{16} = 4$ units
$AD = \sqrt{(4\;-\;0)^{2} + (0\;-\;0)^{2}} = 16 = 4$ units
Step 2: Identify the type of the polygon (regular or irregular) based on the dimensions. Find the perimeter based on the type of the polygon.
In this example, $AB = BC = CD = AD = 4$ units
So, it is a regular polygon.
Perimeter of the polygon $= 4 \times 4 = 16$ units
Facts about Perimeter of a Polygon
- A circle is not a polygon because it is not made of straight lines. The perimeter of a circle is usually called the circumference.
- The smallest polygon that can be formed is a triangle.
Conclusion
In this article, we learned about the perimeter of a polygon and formulas to find the perimeter of regular and irregular polygons. Let’s solve a few examples and practice problems based on these concepts.
Solved Examples on Perimeter of a Polygon
1. What is the perimeter of the polygon in the diagram?

Solution:
All the sides of PQR are of different lengths. It is an irregular polygon.
The perimeter is the total length of its boundary.
We will find its perimeter by adding the lengths of three sides.
Perimeter of $PQR = PQ + QR + PR$
Perimeter of $PQR = 5 + 10 + 8 = 23$ feet
2. What will be the perimeter of a rectangle whose length is 14 inches and breadth is 5 inches?
Solution:
Length of the rectangle, i.e., $l = 14$ inches
Breadth of the rectangle, i.e., $b = 5$ inches
Perimeter of the rectangle $= 2(l + b) = 2(14 + 5) = 2 \times 19 = 38$ inches
3. What will be the perimeter of a regular nonagon whose side is 8 feet each?
Solution:
Number of sides of a regular nonagon $= 9$
Measure of each side $= 8$ feet
Perimeter a regular polygon $=$ (number of sides) $\times$ (measure of each side)
Perimeter of a regular nonagon $= 9 \times 8 = 72$ feet
4. Find the missing length CD of the given polygon if the perimeter of the polygon is 34 units.
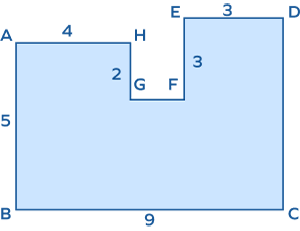
Solution:
$GF = BC – (AH + DE) = 9 – (4 + 3) = 9 – 7 = 2$ units
Perimeter of the polygon $ABCDEFGH = AB + BC + CD + DE + EF + FG + GH + AH$
$34 = 5 + 9 + CD + 3 + 3 + 2 + 2 + 4$
$34 = 28 + CD$
$CD = 34 – 28 = 6$ units
5. Find the perimeter of a square if the area of square is 49 in2.
Solution:
Area of square $= 49\; in^{2}$
$side \times side = 49$
side of square $= 7$ inches
Perimeter of square $= 4 \times side = 4 \times 7 = 28$ inches
6. If the coordinates of a 2D shape is A(2, 5), B(8, 5), C(8, 3), D(2, 3), then which polygon will be formed? Also find the perimeter of the polygon.
Solution:
$AB = \sqrt{(8\;-\;2)^{2} + (5\;-\;5)^{2}} = \sqrt{36} = 6$ units
$BC = (8\;-\;8)^{2} + (3\;-\;5)^{2} = \sqrt{4} = 2$ units
$CD = (2\;-\;8)^{2} + (3\;-\;3)^{2} = \sqrt{36} = 6$ units
$AD = (2\;-\;2)^{2} + (5\;-\;3)^{2} = \sqrt{4} = 2$ units
Since $AB = CD$ and $BC = AD, ABCD$ is either a rectangle or a parallelogram.
Perimeter of the polygon $= 2(AB + BC) = 2(6 + 2) = 16$ units
Practice Problems on Perimeter of a Polygon
Perimeter of a Polygon: Definition, Formula, Examples, Facts, FAQs
If the perimeter of an equilateral triangle is 27 units, then the side will be:
Perimeter of an equilateral triangle $= 27$ units
$3 \times$ side $= 27$ units
side $= 27 \div 3 = 9$ units
Find the perimeter of a regular hexagon if the length of each side is 18 feet.
The length of each side $= 18$ feet
Perimeter of a regular hexagon $= 6 \times 18 = 108$ feet
If the perimeter of a square is 72 yards, then the area of the square will be ____ cm.
Perimeter of a square $= 72$ cm
$\Rightarrow 4 \times side = 72\; cm \Rightarrow side = 18$ cm
Area of a square $= side \times side = 18 \times 18 = 324 cm^{2}$
Find the perimeter of the following polygon.
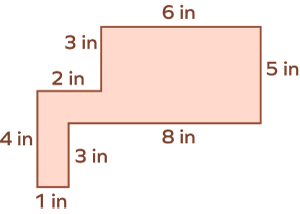
Perimeter of the polygon $= 6 + 5 + 8 + 3 + 1 + 4 + 2 + 3 = 32$ inches
Find the missing side 𝑥 of the following figure if the perimeter of the polygon is 40 units.
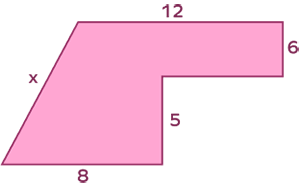
Perimeter of the polygon $= 12 + 𝑥 + 8 + 5 + 6$
$40 = 12 + 𝑥 + 8 + 5 + 6$
$40 = 31 + 𝑥 𝑥 = 40 – 31 = 9$ units
If the perimeter of a square is equal to the area of a square, then the side of the square is _________.
Perimeter of a square $= 4 \times side$
Area of square $= side \times side$
$4 \times side = side \times side$
side $= 4$ units
Frequently Asked Questions on Perimeter of a Polygon
The perimeter of a regular polygon is directly proportional to the length of its side. True or False?
True. The perimeter of a regular polygon is directly proportional to the length of its side. Perimeter of a regular polygon $=$ (number of sides) $\times$ (length of one side). Thus, if the length of the side is increased or decreased, the value of the perimeter also increases or decreases.
What is the formula to calculate the perimeter of an isosceles triangle?
An isosceles triangle has two sides equal. If two equal sides are of measure l and the base is b, then perimeter of the isosceles triangle $= l + l + b = 2l + b$.
Can the perimeter of a square be greater than its area?
The area of a square is given by $(side)^{2}$. Its perimeter is given by 4(side). Thus, for a square, the area is always greater than the perimeter.
Are the perimeters of a regular polygon always even?
No, the perimeter of a regular polygon can be odd as well as even. The perimeter of a regular polygon with an even number of sides will always be even. The perimeter of a regular polygon with an odd number of sides can be odd or even depending on the length of the side.
How do you find the perimeter of a regular polygon with n sides?
Multiply the length of one side by n. Perimeter $= n \times$ (length of a side).
How to find the perimeter of a polygon?
Add all the sides of the polygon to find its perimeter.


























