A rectangular prism is a three-dimensional solid shape with six faces that including rectangular bases.

A cuboid is also called a rectangular prism. The cross-section of a cuboid and a rectangular prism is the same.
Real-Life Examples
A pencil box and a book are rectangular prisms. It may surprise you, but your room is also a cuboid or a rectangular prism.

Recommended Games
Properties of a Rectangular Prism:
- A rectangular prism has 8 vertices, 12 sides and 6 rectangular faces.
- All the opposite faces of a rectangular prism are congruent.
- A rectangular prism has a rectangular cross section.
Types of Rectangular Prisms
There are two types of rectangular prisms:
- Right Rectangular Prism: The angle formed by the faces with any of its bases is 90° or a right angle. All the faces, including the lateral ones, are rectangular.
- Non-Right (Oblique) Rectangular Prism: The faces of such a prism are not at right angles to the bases. The shape of each face is more like a parallelogram than a perfect rectangle.
Surface Area and Volume of a Rectangular Prism:
The rectangular prism has three dimensions. It means that it has a surface area and volume.
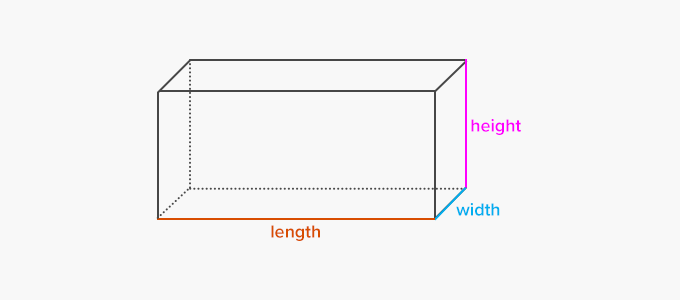
Since all the faces of a rectangular prism are rectangles and opposite faces are equal, the surface area of a rectangular prism can be calculated using the following formula:
Total Surface Area $= 2 {(\text{width} \times \text{length} ) + (\text{length} \times \text{height}) + (\text{width} \times \text{height})}$
Lateral Surface Area $= 2 {( \text{length} \times \text{height} ) + (\text{width} \times \text{height} )}$
Volume of a rectangular prism is simply obtained by multiplying all three dimensions $–$ length, height and width.
Volume $= \text{length} \times \text{width} \times \text{height}$
Fun Facts
| – Rectangular prisms are the most commonly used prisms in real life, especially in packaging, from cereal boxes to cartons and parcels delivered by mail. |
Solved Examples on Rectangular Prism
- Find the volume of a right rectangular prism whose length $= 8$ cm, width $= 5$ cm, and height $= 16$ cm.
Volume $=$ (LWH)
$= 8516$
$= 640$ cm3
- What is the total surface area of a right rectangular prism with length $= 5$ feet, width $= 4$ feet, and height $= 6$ feet.
Total surface area $= 2 { (\text{WL})+(\text{LH})+(\text{WH})}$
Total surface area $= 2 {(45)+(56)+(46)}$
$= 2(20+30+24)$
$= 148$ ft2
- The dimensions of a rectangular prism are length = 2.5 cm, width = 4.5 cm, and height = 1.5 cm. Find the volume.
Volume $=$ LWH
$= 2.5 4.5 1.5$
$= 16.875$ cm3
- For a rectangular prism, length $= 4$ feet, width $= 4$ feet and height $= 9$ feet. Find the lateral surface area.
Lateral surface area $= 2 { (\text{LH})+(\text{WH})}$
Lateral surface area $= 2 { (49)+(49)}$
$= 2 ( 36+36 ) = 144$ ft2
Practice Problems on Rectangular Prism
What is a Rectangular Prism? Definition With Examples
What is the volume of a rectangular prism whose dimensions are length $= 2$ cm, width $= 2$ cm, and height $= 4$ cm?
Volume $= 2 \times 2 \times 4 = 16 \text{cm}^3$
The volume of a rectangular prism is $50 \text{cm}^3$. Also, length $= 2$ cm and width $= 5$ cm. What is its height?
$h$ $= \frac{V}{(l \times w)} =\frac{50}{(2\times5)}=5$ cm
The dimensions of a rectangular prism are length $= 4$ cm, width $= 6$ cm and height $= 10$ cm. What is the total surface area?
Total Surface Area $=$ $2{(4\times6)+(6\times10)+(10\times4)} =248 \text{cm}^2$
The dimensions of a rectangular prism are length $= 5$ cm, width $= 6$ cm and height $= 7$ cm. What is the lateral surface area?
Lateral Surface Area $=$ $2\times{ (5\times7)+(6\times7) } = 154 \text{cm}^2$
Frequently Asked Questions on Rectangular Prism
How many bases does a rectangular prism have?
A rectangular prism has two congruent and parallel rectangular bases.
What is the net of a rectangular prism used for?
The net of the rectangular prism is used to find the total surface area.
Can a right rectangular prism have a square face?
Yes. Some prisms are named according to special properties. A right rectangular prism with a square base is called a right square prism.
What makes a right rectangular prism different from an oblique rectangular prism?
The bases of the right rectangular prism are perpendicular to each other. Whereas the bases of the oblique rectangular prism are not perpendicular.

















