What is a Right Rectangular Prism? Definition With Examples

What Is a Right Rectangular Prism?

In geometry, a rectangular prism can be defined as a 3-dimensional solid shape that has 6 faces with its base as rectangles. Rectangular prisms can be of two types, namely right rectangular prisms and non-right (oblique) rectangular prisms.

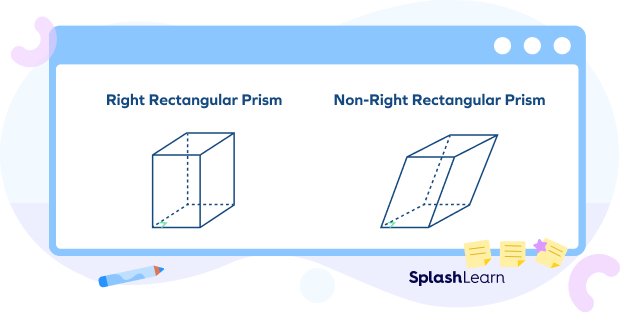
The right rectangular prism has two parallel end faces and four lateral faces, each one of which is a rectangle; the faces are perpendicular to each of its bases. The faces of a non-right rectangular prism (oblique prism) are parallelograms. 

A right rectangular prism is also called a cuboid.

We can find the shape of a right rectangular prism all around us—in a truck, a chest of drawers, and an aquarium. 

Properties of a Right Rectangular Prism:

• It has 8 vertices, 12 sides, and 6 rectangular faces.
• All its opposite faces are congruent. 
• The angle between its base and sides is 90 degrees or right angle.
• All its faces are rectangles and parallel.

Surface Area and Volume of a Right Rectangular Prism

Let’s consider this right rectangular prism with the marked length, width, and height. 

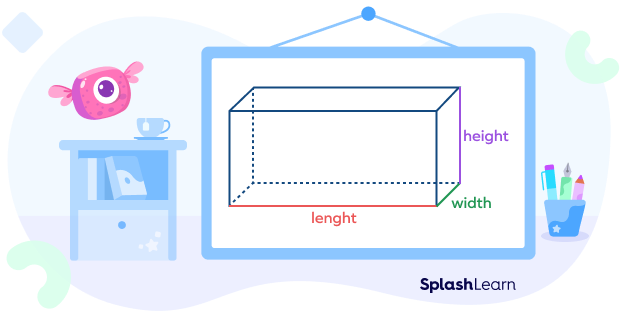
Since all its faces are rectangles and opposite faces are equal, the surface area of a right rectangular prism can be calculated using the following formula:

Lateral Surface Area = 2 × height (length + width) Total Surface Area = 2 {( width × length )+( length × height ) + (width × height )}

Volume of a right rectangular prism is obtained by multiplying all three dimensions—length, height, and width—or by multiplying the base area with its height.

Volume = length ×  width × height OR Volume = Area of base × height

Fun Facts

Rectangular prisms are the most commonly used prisms in real life, especially in packaging—from cereal boxes to cartons and parcels delivered by mail.  

Solved Examples

Example 1: Find the volume of the given cuboid.

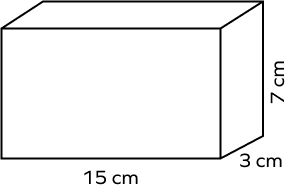
Solution:

length = 15 cm; width = 3 cm; height = 7 cm

Volume = length × width × height

= 15 × 3 × 7 cm³

= 315 cm³

Example 2: Find the volume of the rectangular prism with a base area of 105 square meters and a height of 4 meters.

Solution: 

Volume = Area of base × height

= 105 × 4 m³

= 420 m³

Example 3: A foam company manufactures mattresses. Their king-sized mattress is approximately 183 cm by 183 cm, with a thickness of 12.5 cm. Find the total surface area of the mattress.

 Solution: 

length = 183 cm

width = 183 cm

height = 12.5 cm

Total surface area = 2 {(width × length) + (length × height) + (width × height)}

= 2 {(183 × 183) + (183 × 12.5) + (183 × 12.5)} cm²

= 2 {33,489 + 2,287.5 + 2,287.5} cm²

= 2 {38,064} cm²

= 76,128 cm²

Example 4: Find the area of an iron sheet required to construct a closed container of length 5 m, height 6.5 m and width 2.3 m.

Solution: 

To find the iron sheet required, we need to find the total surface area of a cuboid with the given dimension.

Total surface area = 2 {(width × length) + (length × height) + (width × height)}

= 2 {(2.3 × 5) + (5 × 6.5) + (2.3 × 6.5)} m²

= 2 {(11.5) + (32.5) + (14.95)} m²

= 2 {58.95} m²

= 117.9 m²So, a 117.9 m² iron sheet is required to construct the container.

Practice Problems

Lateral surface area = 2 { (L $\times$ H) + (W $\times$ H)}

Lateral surface area = 2 { (4 $\times$ 9) + (4 $\times$ 9)}

= 2 ( 36 + 36 ) = 144 ft²

Practice Problems

Frequently Asked Questions