If we look at the world around us, we can see various 2D and 3D shapes. Having a basic knowledge of different shapes in our everyday lives can serve as a stepping stone for advanced mathematical learning. One such shape is the pyramid.
When you hear the word pyramid, what is the first thing that comes to your mind? The chances are that you may be thinking about the famous pyramids of Egypt. Apart from those ancient structures, several other things around us have that shape.
What Is a Pyramid?
A pyramid is a three-dimensional figure. It has a flat polygon base. All the other faces are triangles and are called lateral faces. The number of lateral faces equals the number of sides on its base. Its edges are the line segments formed by two intersecting faces. The vertex is the common point where three or more edges combine. Except for the base, all the faces connect at a vertex at the top called the apex. The apex stands opposite to the base and provides it a shape.

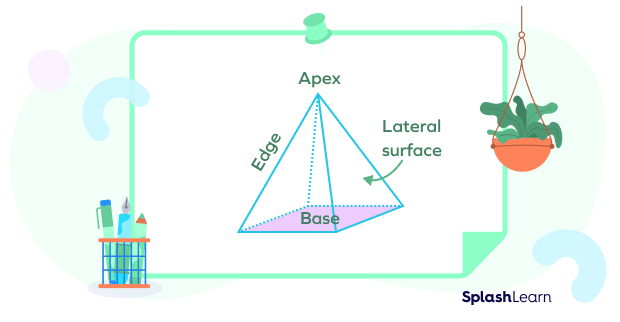
Fun Fact: The polygon base of a pyramid is a square in maximum cases.
Pyramid Examples in Real Life
A famous example in real life is the Great Pyramid of Giza in Egypt. This three-dimensional geometric shape is among the largest and oldest pyramids existing today. Chichen Itza in Mexico is another such example.

Recommended Worksheets
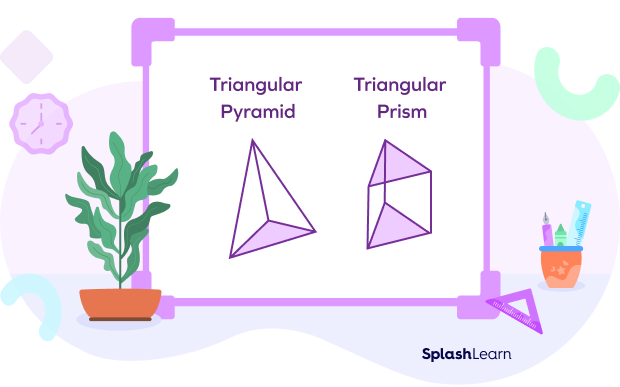
Differences between Pyramid and Prism
Pyramids and prisms are both three-dimensional figures with polygonal bases and flat faces. But they have several differences, such as:
- While a pyramid has a single base, a prism has two of them.
- A pyramid has triangular faces, but a prism has rectangular faces.
- A pyramid has an apex. A prism has no apex.
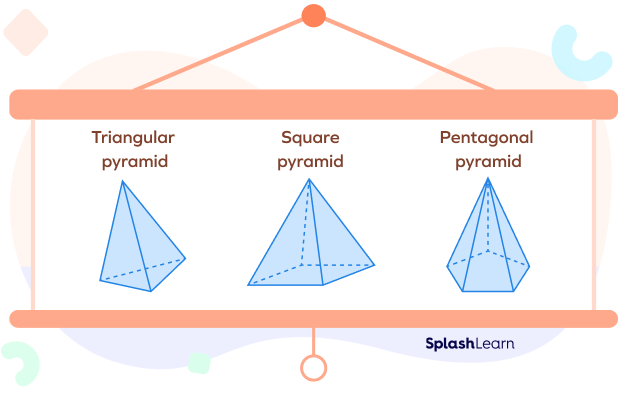
Types of Pyramids
The type depends on the shape of its base. Some examples are triangular, square, and pentagonal pyramids.
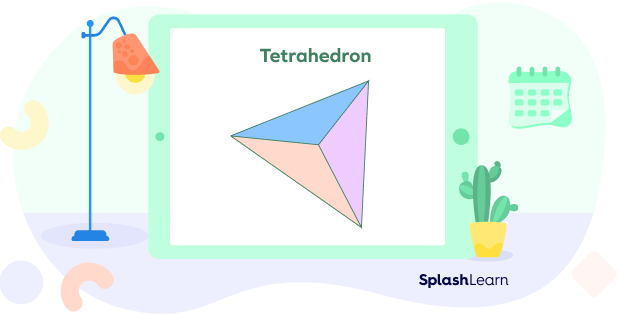
Tetrahedron
A triangular pyramid that has all its sides equal is called a tetrahedron. The tetrahedron is the only pyramid in which any face can be considered the base and any vertex the apex.
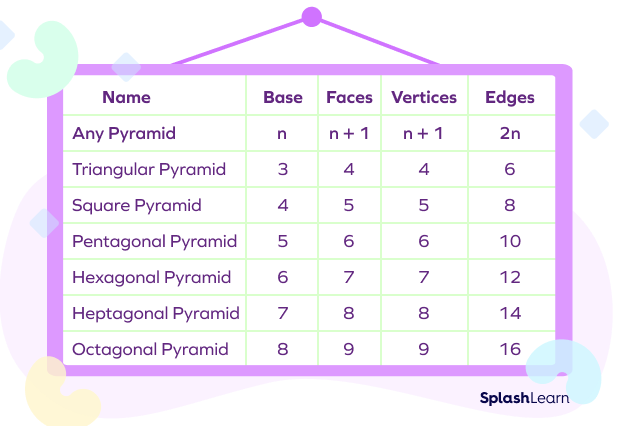
Number of Faces, Vertices, and Edges
A pyramid with a base of n sides has n+1 faces, n+1 vertices, and 2n edges.
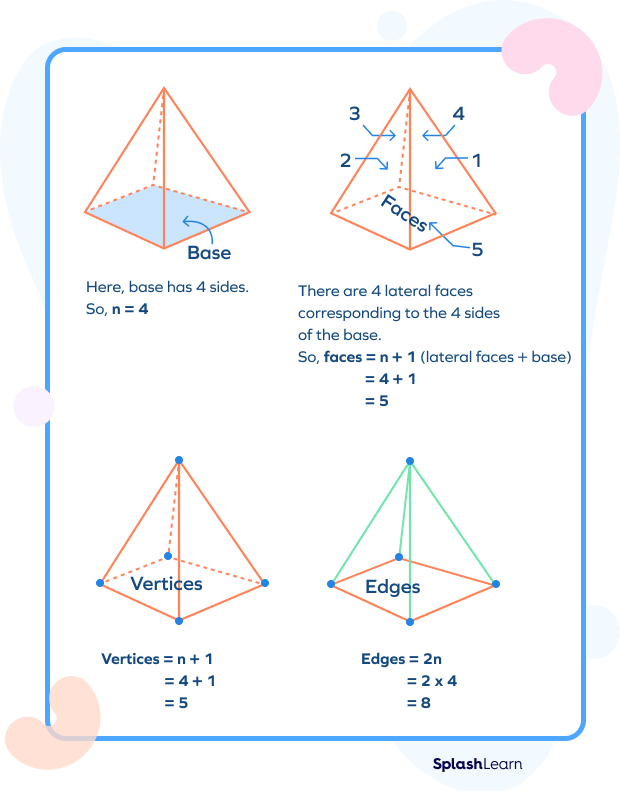
So, for a square pyramid,
No. of sides in the base = 4
No. of faces = (4 + 1) = 5
No. of vertices = (4 + 1) = 5
No. of edges = 2(4) = 8
What Are Right and Oblique Pyramids?
The position of the top or apex tells us if it is a right or an oblique pyramid.
Right Pyramid
You can find the apex located exactly over the center of the base in the right pyramid. If you draw a perpendicular line from the apex to the base, it will intersect the center of the base.
Oblique Pyramid
You can find the apex located slightly away from the mid-point of the base in the oblique pyramid. If you draw a perpendicular line from the apex to the base, it won’t intersect the center of the base.

What Are Regular and Irregular Pyramids?
A pyramid with regular polygon as a base is called a regular pyramid. It means all the sides and angles of the base polygon are equal.
Examples include a pyramid with an equilateral triangle or a square as a base.

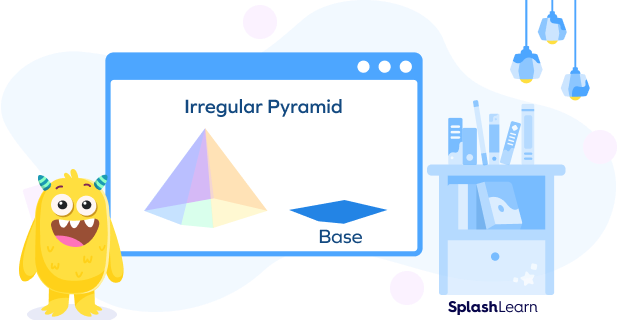
A pyramid with an irregular polygon as a base is called an irregular pyramid. In it, the sides of the base polygon are unequal.
Examples include a pyramid with a scalene triangle or a rectangle as a base.
Volume of a Pyramid
The volume is the amount of space enclosed within its faces. We measure it in cubic units.
Volume = 1/3 × Base Area × Height
Surface Area of a Pyramid
The surface area is the total area covered by all its faces.
The formula used to find the surface area of a pyramid varies depending on the pyramid type. We measure the surface area in square units.
For a pyramid with all side faces that are equal:
Surface Area = Base Area + (½ × perimeter of the base × Slant height)
For a pyramid with different side faces:
Surface Area = Base Area + Lateral Area
To find the surface area of a pyramid where the side faces are unequal, we need to find the total lateral area first. We do this by adding the area of each lateral face.
Solved Examples
Example 1: Calculate the volume of a pyramid that has a base area of 65 units and a height of 9 units.
Solution: Here, base area = 65 and height = 9
Volume (V)= 1/3 × Base Area × Height
V= 1/3 × 65 x 9
V= 195 cube unit
The pyramid has a volume of 195 cube units.
Example 2: What is the surface area of a square pyramid that has a base side of 12 inches and a slant height of 20 inches?
Solution: Here, the perimeter of the base = 4 × 12 = 48 inches.
Base area = 12×12 = 144 square inches.
Slant height = 20 inches.
Surface Area (S) = Base Area + (½ × Perimeter of the base × Slant height)
S = 144 + (½ × 48 × 20)
S = 624 sq.inch.
The square pyramid has a surface area of 624 sq. inch.
Example 3: Determine the length of the base side of a square pyramid that has a volume of 16 cubic feet and a height of 12 feet.
Solution: Volume = 16; Height = 12
Volume (V) = 1/3 × Base Area × Height
=>16 = 1/3 × Base Area × 12
=> Base Area = 16 x 3 x 1/12 = 4 sq. feet.
The side of the square pyramid base = √4 = 2 sq. feet.
Practice Problems
Pyramid - Definition with Examples
How many edges does an octagonal pyramid have?
A pyramid has 2n edges, where n= number of sides.
Since an octagonal pyramid has 8 sides, it has 2x8 = 16 edges.
What is the volume of a pyramid that has a base area of 37 units and a height of 12 units?
Volume (V)= 1/3 × Base Area × Height
Here, base area = 37 and height = 12
Volume = 1/3 × Base Area × Height = 1/3 x 37 x 12 = 148 cubic units
What is the surface area of a square pyramid that has a base side of 8 inches and a slant height of 26 inches?
Surface Area (S) = Base Area + (½ × perimeter of the base × Slant height)
Here, the perimeter of the base = 4 × 8 = 32 inches.
Base area = 8x8 = 64 square inches.
Slant height = 26 inches.
So, surface area (S) = 64 + (1/2 x 32 x 26) = 480 sq.inch.
Frequently Asked Questions
Is a pyramid a polyhedron?
Yes, a pyramid is a polyhedron.
What is a star pyramid?
A star pyramid has a regular star-shaped polygon as a base.
What will we call a hexagonal pyramid base with equilateral triangle faces?
A heptahedron.



















