What is a Polyhedron?
We know that a polygon is a flat, plane, two-dimensional closed shape bounded by line segments. Common examples of polygons are square, triangle, pentagon, etc.
Now, can you imagine a three dimensional figure with faces in the shape of a polygon? Such a three-dimensional figure is known as a Polyhedron. Examples you must be familiar with are diamonds, rubik’s cube, pyramids, etc.
Polyhedron Definition
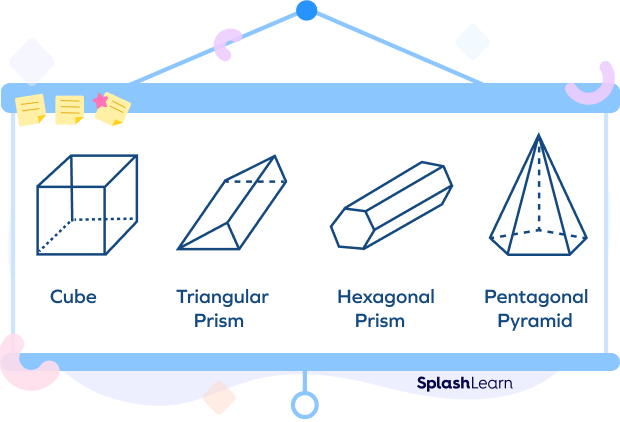
A three-dimensional shape with flat polygonal faces, straight edges, and sharp corners or vertices is called a polyhedron.
Common examples are cubes, prisms, pyramids. However, cones, and spheres are not polyhedrons since they do not have polygonal faces.
The plural of a polyhedron is called polyhedra or polyhedrons.
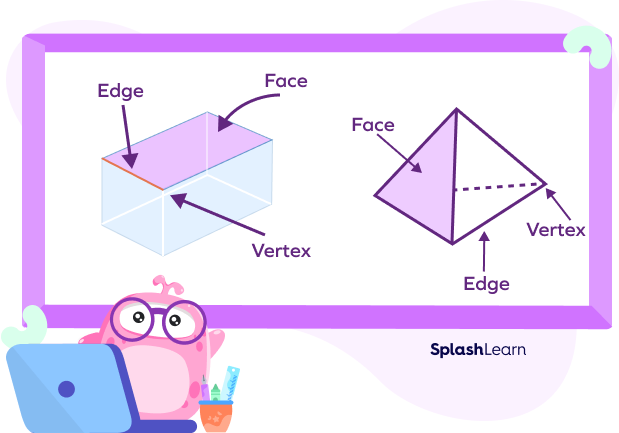
Faces, Edges, and Vertices
The parts of a polyhedron are classified as faces, edges, and vertices.
- Polyhedron Faces: The flat surfaces of a polyhedron are termed as its faces, which are basically polygons.
- Polyhedron Edges: Edges are the line segments where two faces meet.
- Polyhedron Vertices: The point of intersection of two edges is known as a vertex.
The figure given below will give us a better view:
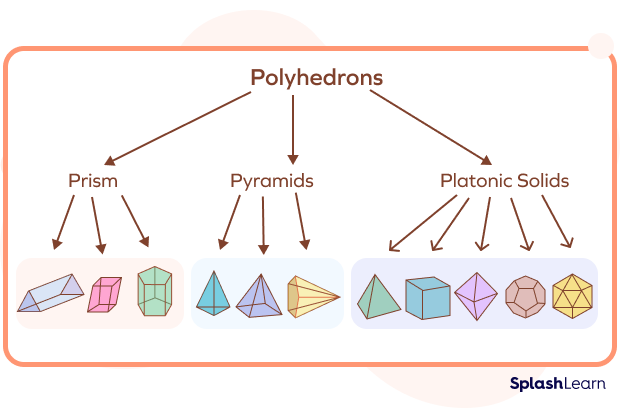
Prisms, Pyramids, and Platonic Solids
Polyhedrons can be broadly classified as prisms, pyramids, and Platonic solids. Let’s understand each type.
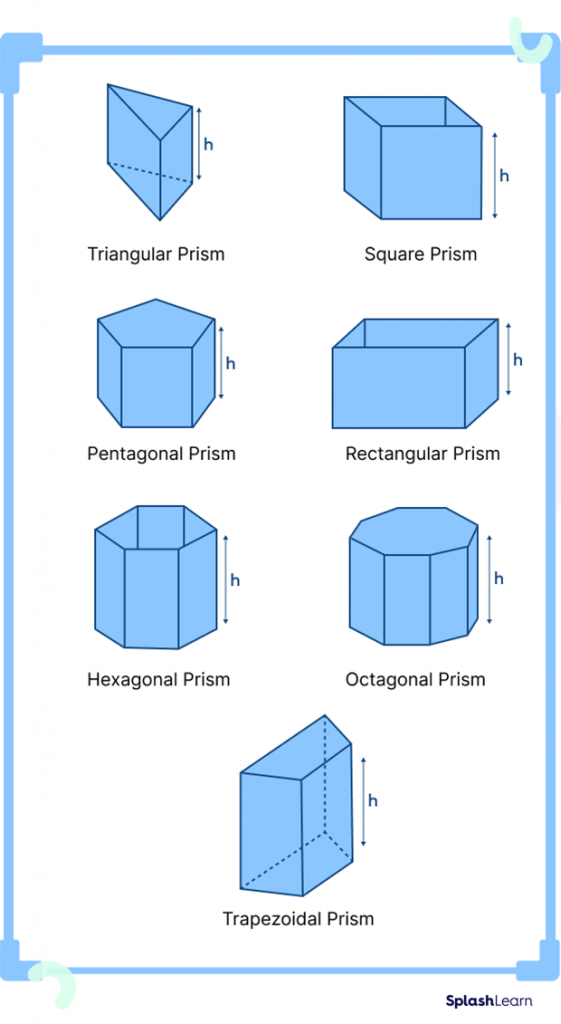
1. Prism
A prism has its both ends (base and top) as identical polygons and its side faces are flat (rectangles or parallelograms). Prisms are named after its base, which can be a triangle, square, rectangle, or any n-sided polygon.
2. Pyramid
A pyramid has its base as any polygon and its side faces are triangles with a common vertex (known as apex). If the base of a pyramid is an n-sided polygon, then it has (n+1) faces, (n+1) vertices, and 2n edges.
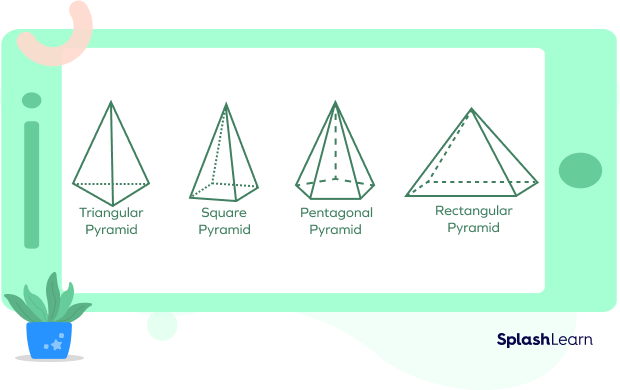
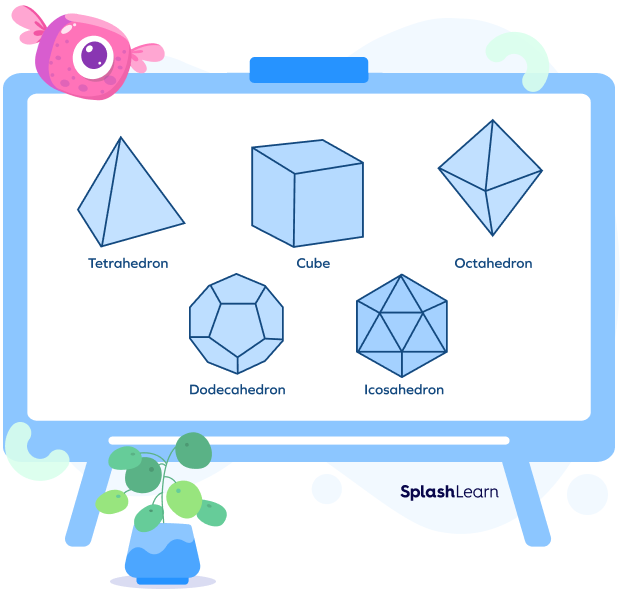
3. Platonic Solids
In Platonic solids, all the faces are congruent regular polygons and the same number of faces meet at each vertex.
Examples in Real Life
We can observe several polyhedra in our daily existence such as a Rubik’s cube, dice, buckyball, pyramids, and so on. A diamond is one of the real-life examples of polyhedron.

Types of Polyhedron
Polyhedra are mainly divided into two types based on the polygonal faces and the base — regular polyhedrons and irregular polyhedrons. Platonic solids are regular polygons. Prisms and pyramids are irregular polyhedrons.
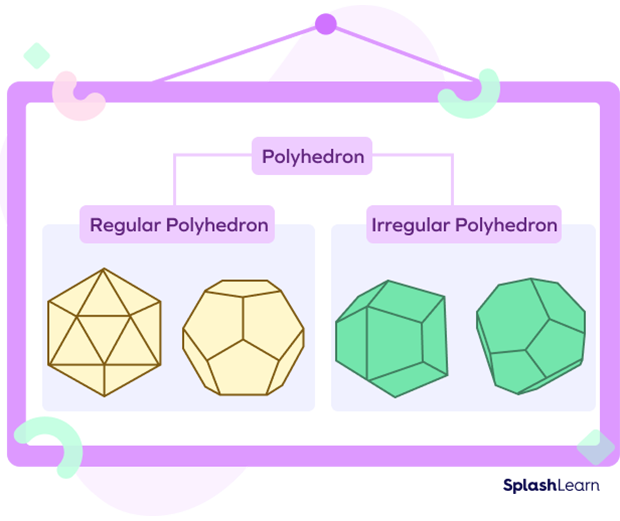
Regular Polyhedron
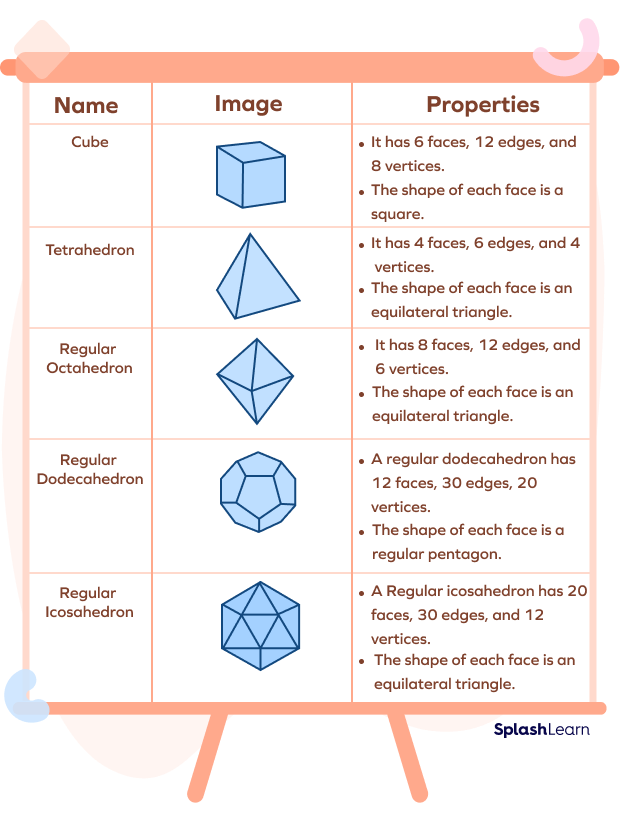
Regular polyhedrons are made up of regular polygons. They are also known as “Platonic solids.” They have all their faces, edges, and angles congruent. The following is the list of the five regular polyhedrons:
Irregular Polyhedron
An irregular polyhedron has polygonal faces that are not congruent to each other. It is made up of polygons having different shapes. So, all its components are not the same.
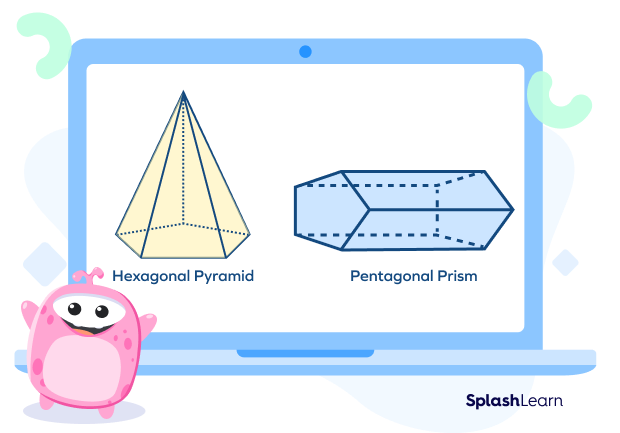
Polyhedrons can also be divided into convex and concave categories, just like polygons.
Convex Polyhedron
A convex polyhedron is similar to a convex polygon. If a line segment that joins any two points on the surface lies inside the polyhedron, then it is known as a convex polyhedron. All platonic solids are convex.
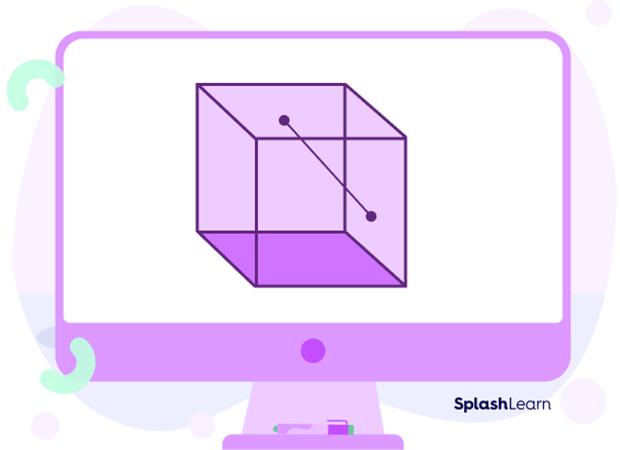
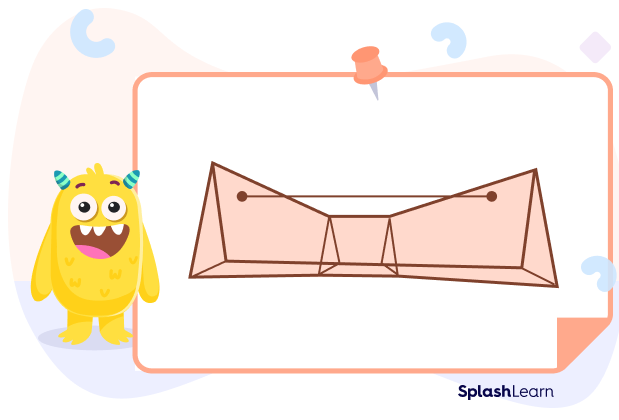
Concave Polyhedron
A concave polyhedron is similar to a concave polygon. If a line segment that joins any two points on the surface lies outside the polyhedron, it is known as a concave polyhedron.
Euler’s Formula
There is a relationship between the number of faces, edges, and vertices in a polyhedron, which can be presented by a math formula known as “Euler’s Formula.”
$\text{F} + \text{V}$ $–$ $\text{E} = 2$
where,
$\text{F} =$ number of faces
$\text{V} =$ number of vertices
$\text{E} =$ number of edges
If we know any two values among F, V, or E, we can find the third missing value using Euler’s formula. So, the questions like ‘How many edges does a polyhedron have?’ or ‘How many faces does a polyhedron have?’ can be answered easily if the other two values are known. We can also check if a polyhedron with the given number of parts exists or not.
For example, a cube has 8 vertices, 6 faces, and 12 edges.
$\text{F} = 6, \text{V} = 8, \text{E} = 12$
Applying Euler’s formula, we get $\text{F} + \text{V}$ $–$ $\text{E} = 2$
Substituting the values in the formula: $6 + 8$ $–$ $12 = 2 \Rightarrow 2 = 2$.
Hence, the cube is a polyhedron.
Solved Examples on Polyhedron
1. How many types of regular polygons are there?
Solution: There are 5 types of regular polygons: tetrahedron, cube, octahedron, dodecahedron, and icosahedron.
2. Check if the polyhedron with 10 vertices, 8 edges, and 4 faces exists or not.
Solution: We will apply Euler’s formula:
$\text{V} = 10, \text{E} = 8$, and $\text{F} = 4$
$\text{F} + \text{V}$ $–$ $\text{E} = 4 + 10$ $–$ $8 = 6 ≠ 2$.
The polyhedron with the given dimensions does not exist.
3. How many faces does a polyhedron with 12 vertices and 18 edges have?
Solution: $\text{V} = 12$, $\text{E} = 18$, and $\text{F} =$ ?
By applying Euler’s formula, we get
$\text{F} + \text{V}$ $–$ $\text{E} = 2$
$\Rightarrow\text{F} + 12$ $–$ $18 = 2$
$\Rightarrow\text{F} = 8$
Number of faces = 8
Practice Problems on Polyhedron
Polyhedron - Definition With Examples
Which of the following is not a polyhedron?
Cone is not a polyhedron as the faces of the cone are curved.
Which of the following is a concave polyhedron?
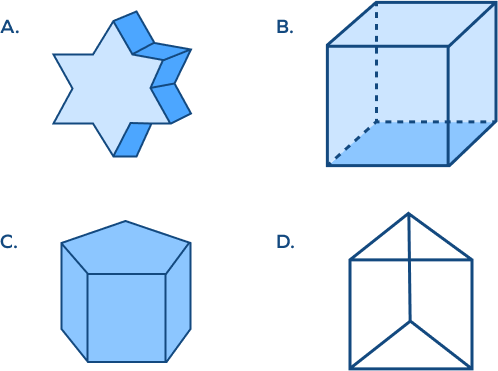
If we draw a line from one face to another, the line will lie outside the polyhedron.
Which of the following combinations will not form a polyhedron?
$\text{F} + \text{V}$ $–$ $\text{E} = 7 + 13 – 15 = 5 ≠ 2$
Which of the following is not a regular polyhedron?
The Hexagonal pyramid does not have all the faces congruent to each other. So, it is not regular.
Frequently Asked Questions on Polyhedron
What is the difference between a polygon and a polyhedron?
A polygon is a two-dimensional figure, which is made up of line segments. For example, square, triangle, hexagon, etc.
On the other hand, a polyhedron is a three-dimensional figure that is made up of polygons. For example, tetrahedron, cube, etc.
Is a cylinder a polyhedron?
No, the cylinder is not a polyhedron as the faces of the cylinder are curved.
What is the difference between a pyramid and a prism?
Both a prism and a pyramid are three dimensional solids that have flat faces and bases. The main difference is that a prism has its two bases (top and bottom) identical whereas a pyramid has only one base.
















