What is a Coordinate Plane?
A coordinate plane is a two-dimensional plane formed by the intersection of two number lines. One of these number lines is a horizontal number line called the x-axis and the other number line is a vertical number line called the y-axis. These two number lines intersect each other perpendicularly and form the coordinate plane that looks like this:
The plane is called two-dimensional because anywhere on this plane where you can put your finger, the location of that point will need two things– its distance on the x-axis and its distance on the y-axis.
The left and the bottom part of the plane have negative x-axis and negative y-axis for negative integers. The point where the number lines intersect is called the origin.
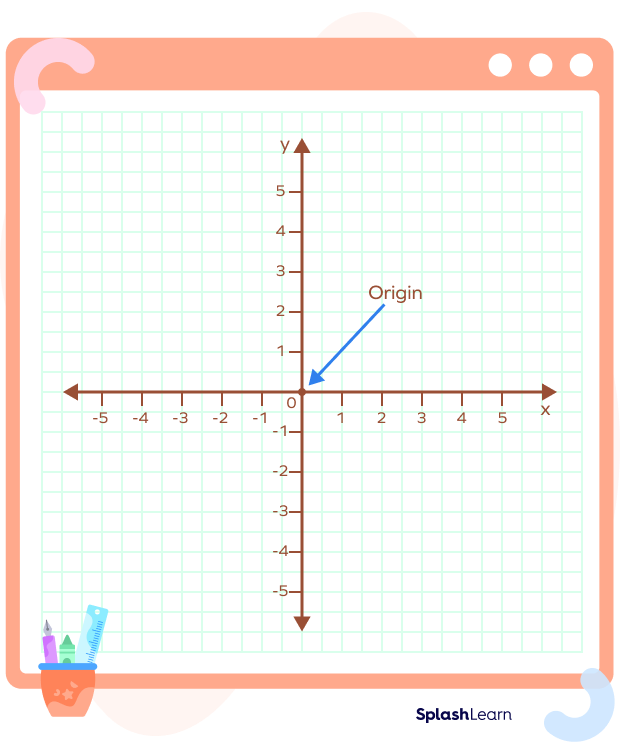
A coordinate plane is a tool used for graphing points, lines, and other objects. It functions like a map that follows directions from one point to another.
Recommended Games
Elements of the Coordinate Plane
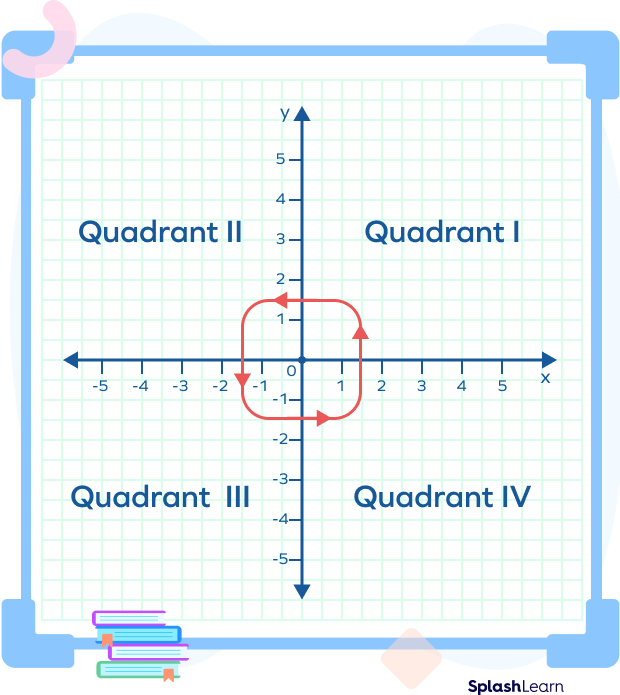
Quadrants: The two number lines divide the coordinate plane into 4 regions. These regions are called Quadrants. The quadrants are denoted by roman numerals and each of these quadrants have their own properties.
Quadrant I: The upper right Quadrant is the first Quadrant denoted as Quadrant I. In this quadrant, the x-axis and the y-axis both have positive numbers.
Quadrant II: The upper left Quadrant is the second Quadrant denoted as Quadrant II. In this quadrant, the x-axis has its negative numbers and the y-axis has positive numbers.
Quadrant III: The bottom left Quadrant is the third Quadrant denoted as Quadrant III. In this quadrant, both the x-axis and the y-axis have negative numbers.
Quadrant IV: The bottom right Quadrant is the fourth Quadrant denoted as Quadrant IV. In this quadrant, the x-axis has positive numbers and the y-axis has negative numbers.
Coordinate: Every point on the coordinate plane is expressed in the form of the ordered pair (x,y) where x and y are numbers that denote the position of the point with respect to the x-axis and the y-axis respectively.
For example: Consider the point A in the given image:
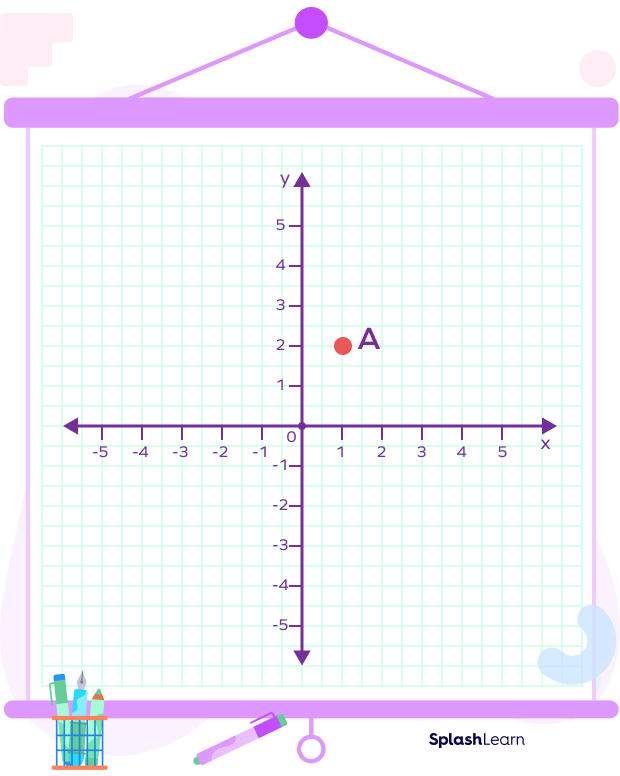
If we want to convey the position of point A, we will check where it lies with respect to the x- and y-axis respectively.
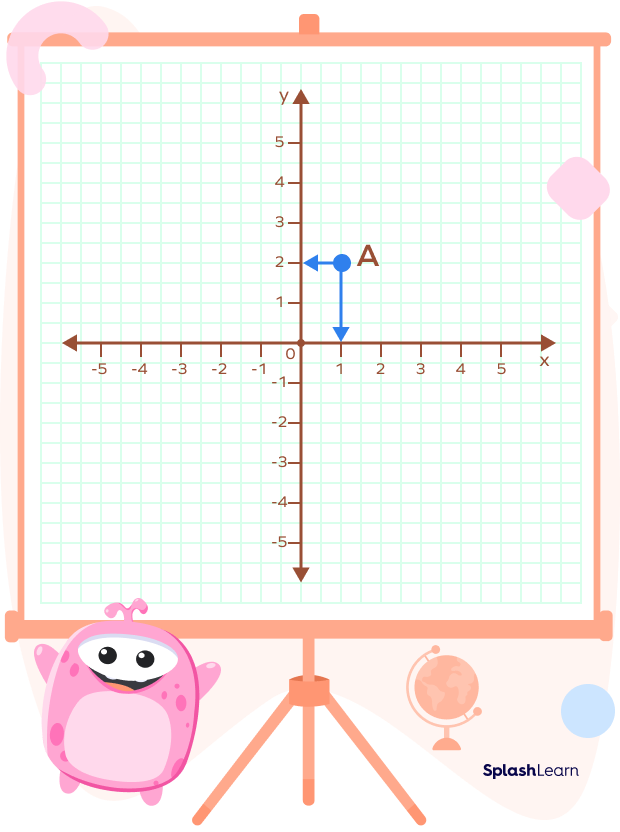
Here the position of A on x-ais is 1 unit and on y-axis is 2 units, therefore we will write the position of A as A(1,2) on the coordinate plane.
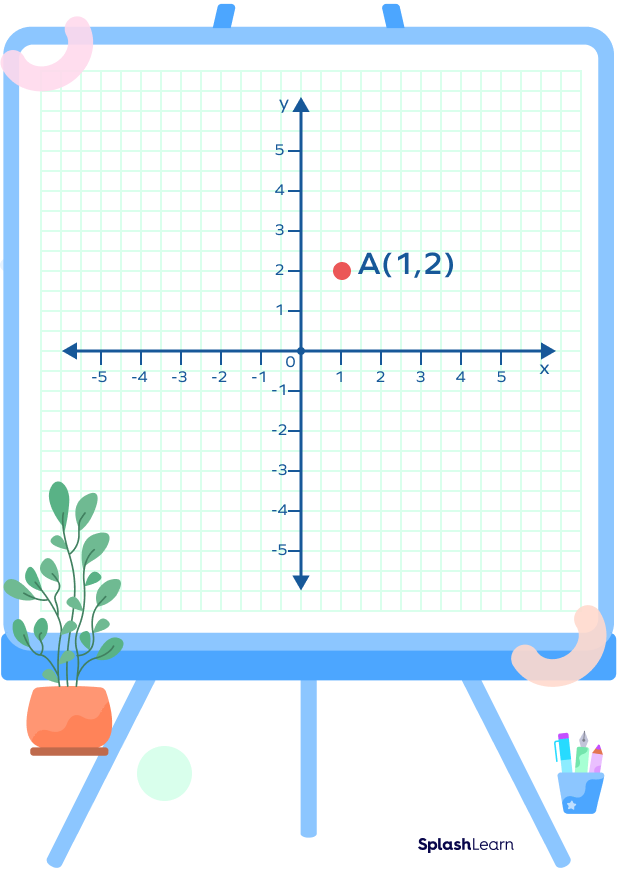
In a similar way, we can find the position of any point on the coordinate plane and it may take values positive or negative depending on the quadrant it lies in. The origin, obviously; is denoted as (0,0)
Recommended Worksheets
Fun Facts
- The coordinate plane was created hundreds of years ago. The system is commonly referred to as the Cartesian coordinate system because French mathematician René Descartes invented it.
- The points on the x-axis have their y-coordinate 0 so the points on x-axis are represented as (x,0) and similarly the points on y-axis have their x-coordinate 0, so they are represented as (0,y).
Conclusion
A coordinate plane is a graphing and description system for points and lines. A vertical (y) axis and a horizontal (x) axis make up the coordinate plane. There are four quadrants in the coordinate plane. The point where these lines connect is called the origin (0, 0). Head over to SplashLearn to know more about the concepts of a coordinate plane.
Solved Examples on Coordinate Plane
Q 1. In which quadrants of the coordinate plane do the following points lie?
● A (–2, 4)
● B (2.5, 3.5)
● C (4, –2.2)
● D (6.5, 1)
Solution:
Point A lies in the second quadrant.
Points B and D lie in the first quadrant.
Point C lies in the fourth quadrant.
Q 2. Which of the following points lie on the y-axis? Explain your answer.
(i) (0, 3)
(ii) (5, 0)
(iii) (–2, 0)
(iv) (0, –2)
(v) (–1, 3)
Solution: (i) and (iv) lie on the y-axis as the x-coordinate is zero in these points.
Q 3. You are at (−4, 3). Move 5 units right and 2 units up. Write the coordinates of point where you reach.
Solution:
Moving 5 units to right will reach on −4 + 5 = 1 on x-axis.
Moving 2 units up will reach on 3 + 2 = 5 on y-axis.
So coordinates of point where we reached is (1, 5).
Q 4. What is the coordinates of point lying on origin?
Solution:
Since point is on origin the coordinates of the point is (0, 0).
Practice Problems on Coordinate Plane
Coordinate Plane
Which of the following points lies in the third quadrant?
Since the points in the third quadrant have both their x and y coordinate as negative numbers.
Which of the following points lies in the first quadrant?
P (2, 5). Here, the abscissa and the ordinate of the point are positive. So, it lies in the first quadrant.
Which of the following point lies on x - axis?
For the point on x - axis, ordinate should be zero.
Start at point (0,0). Go left four spaces. Then, go up five spaces. What point do you land on?
From (0,0) as we go left four spaces we land on coordinate (–4, 0) on X-axis, now from here we go up five spaces we will land on coordinate (–4, 5)
What is the relation between the x-axis and y-axis on the coordinate plane?
The two lines intersect each other perpendicularly at the origin and form the coordinate plane
Frequently Asked Questions on Coordinate Plane
On a coordinate plane, what is the origin?
The origin of the coordinate plane is the location at zero where its two axes cross each other perpendicularly. The origin’s coordinates are (0, 0).
What is the meaning of a coordinate?
A coordinate is an ordered pair of values x and y that helps locate a point on the plane denoted as (x,y).
When is a coordinate plane useful?
When planning the arrangement of different furniture pieces in a space, a two-dimensional grid is made to represent the room. An acceptable unit of measurement can be employed for this. Another example is Air traffic is managed and regulated by using coordinate geometry. Coordinates of the flight are used to describe its current location of the aircraft.
























