Definition of Origin in Math
In mathematics, especially in the field of coordinate geometry; origin is said to be the initial point or the starting point from where we begin our calculations or measurements.
On a ruler, the 0 is from where we start our measurements; hence it is said to be the origin of the scale.
On a weighing machine, we measure our weight when the scale shows zero.
In terms of temperature, when we go below 0 degrees Celsius, it starts getting colder whereas above 0 it starts getting hotter. Hence, it is the point from where we start our measurements.
Origin on the Number Line
The origin on the number line is defined as 0. It divides the number line into two parts as given below:
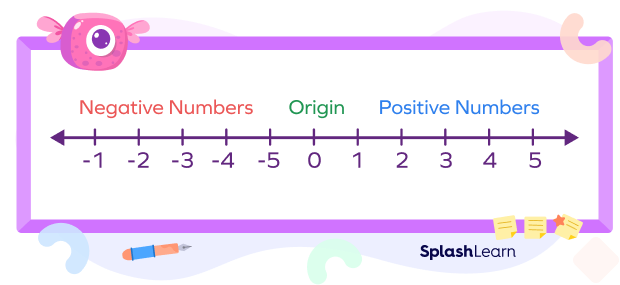
On the left side of origin, we have the negative numbers and on the right side, we have the positive numbers. Whenever we say that we have started from a point, we always say that we have started from 0 or origin.
The origin, i.e., 0, is greater than the negative numbers and smaller than the positive numbers.
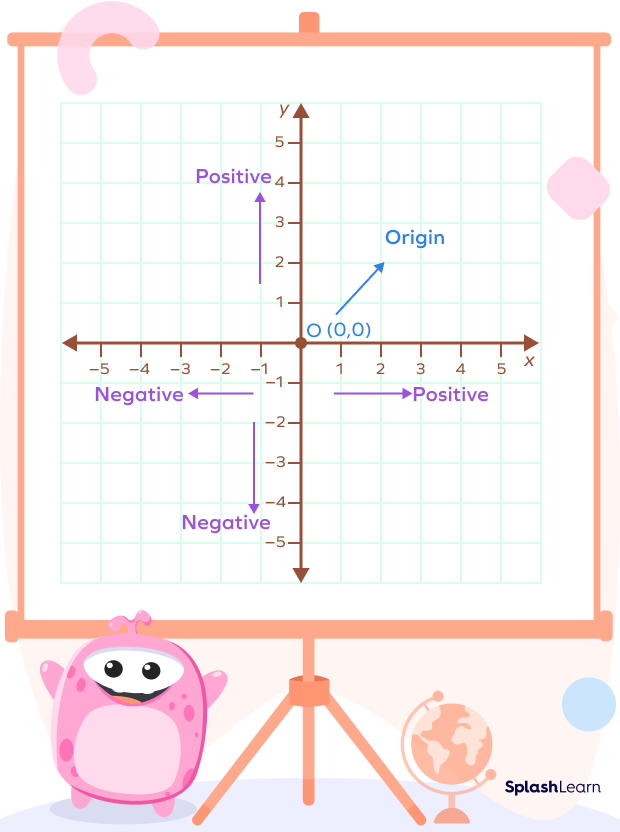
Origin in the Cartesian Plane
The Cartesian Plane is a plane formed by the two number lines—vertical and horizontal. The point at which these two number lines intersect each other is known as the point of intersection which is also known as the origin. It is denoted by the letter O, which is used as a fixed point of reference for the geometry of the surrounding plane. The coordinates of the origin are denoted by (0, 0). It means that at origin, x=0 and y=0. The origin divides each of these axes into two halves—positive and negative.
Distance of a point from the origin
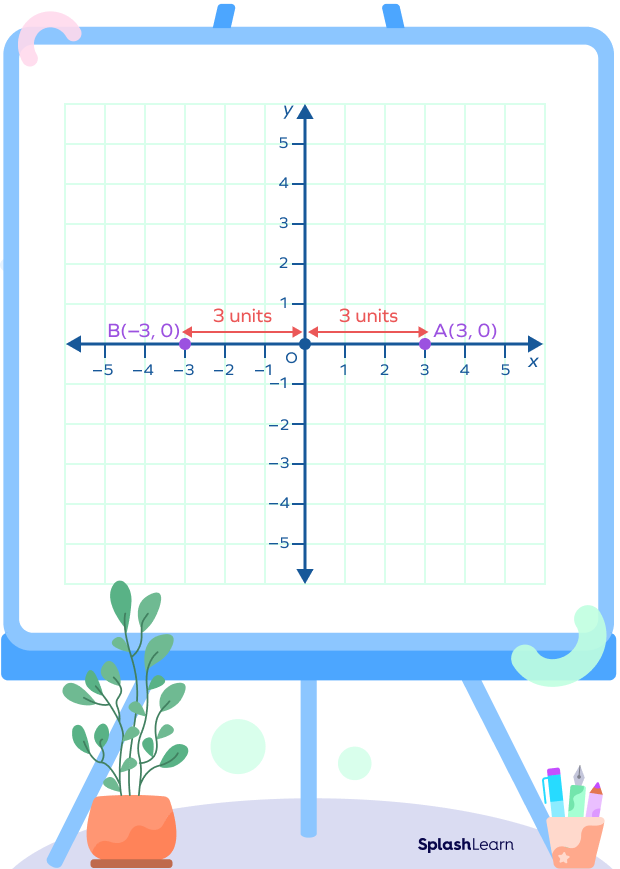
- Point lies on the x-axis.
Any point on the x axis is of the form (x, 0). Its distance from the origin will just be x units.
Consider two points, A(3, 0) and B(–3, 0). Now let’s find their distance from the origin.
Distance of A(3, 0) from the origin = |3| units = 3 units
Distance of B(–3, 0) from the origin = |–3| units = 3 units
This means that the distance of both the points is 3 units from the origin.
The reason for applying the absolute value sign is because distance cannot be negative.
- Point lies on the y-axis.
Any point on the y axis is of the form (0, y). Its distance from the origin will just be y units.
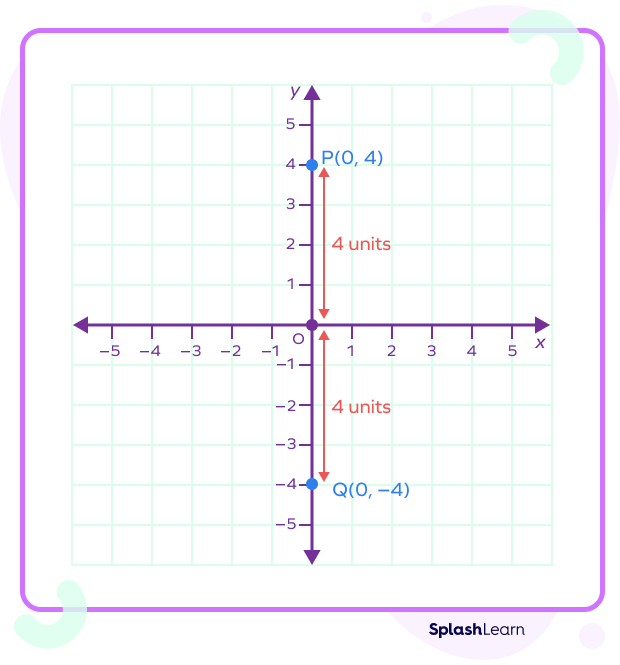
Any point on the y-axis is of the form (0, y). Its distance from the origin will just be y units.
Consider two points, P(0, 4) and Q(0, –4). Now let’s find their distance from the origin.
Distance of P(0, 4) from the origin = |4| units = 4 units
Distance of Q(0, –4) from the origin = |–4| units = 4 units
So, these points are also equidistant from the origin.
Equation of Line Passing through the Origin
The lines that pass through the origin are of the form y = mx where m is a constant. Here, “m” can be rational or irrational.
Let’s consider the equation: y = 2x. To plot this equation on the graph, we substitute a value of x in the equation to get the corresponding value of y. These values of x and y form the ordered pair (x, y). We repeat this for different values of x to get at least 3 ordered pairs. We may record our values in tabular form.
| y = 2x | |||
| x | 1 | 2 | –3 |
| y | 2 | 4 | –6 |
On plotting the graph, we will get a straight line passing through the origin.
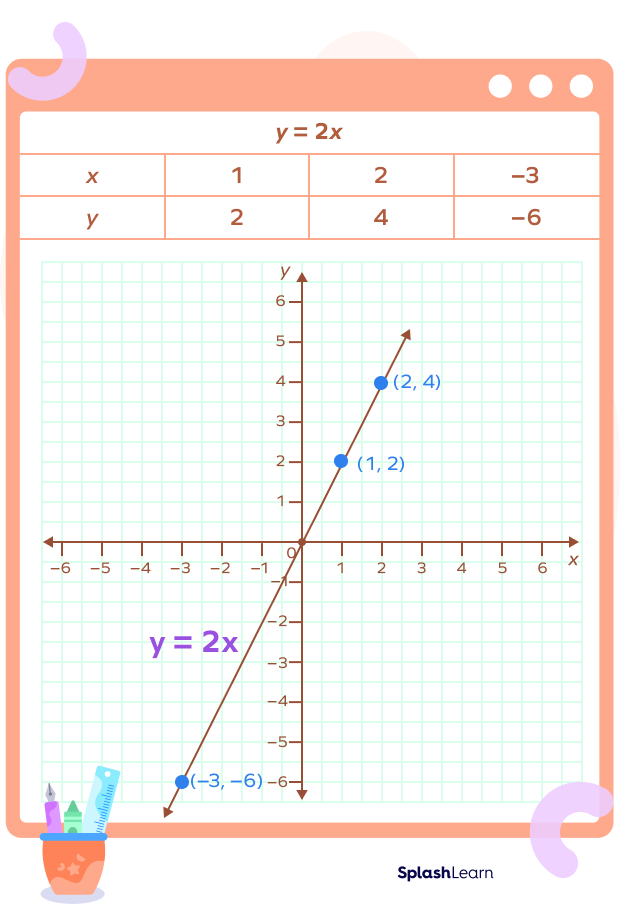
Origin Facts
We can check if the graph of an equation will pass through the origin by substituting x = 0 in the equation. If you get y = 0, then the line of the equation will pass through the origin.
Solved Examples
Example 1: Find the distance of the point from the origin on a number line.
Solution: The distance of the point -10 from the origin, i.e., 0 on a number line =10 units
2. Find the distance of the point (0, -7) from the origin.
Solution: The distance of (0, -7) from (0, 0)=-7=7 units
3. What is the origin of the Cartesian Plane? Solution: In the Cartesian Plane, the point at which the two axes meet is known as origin. The coordinates of the origin are denoted by (0, 0).
Practice Problems
Origin in Math - Definition With Examples
Which of the following is not an equation of line passing through the origin?
$y=-3x+1$ is not an equation passing through the origin as when we substitute
$x=0$, we don’t get $y=0$.
What are the coordinates of the origin on the Cartesian Plane?
On the Cartesian Plane, the origin is denoted by (0, 0), which implies $x = 0$ and $y = 0$.
Which of the following is a graph of a line passing through the origin?
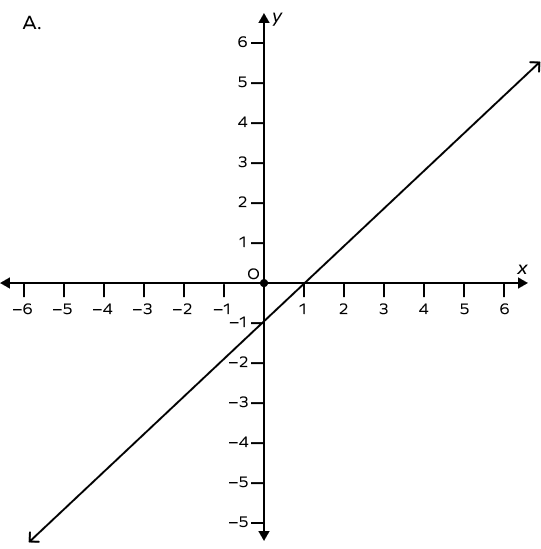
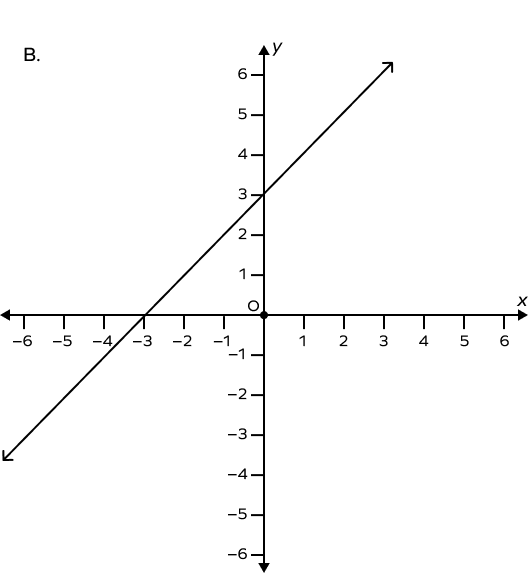
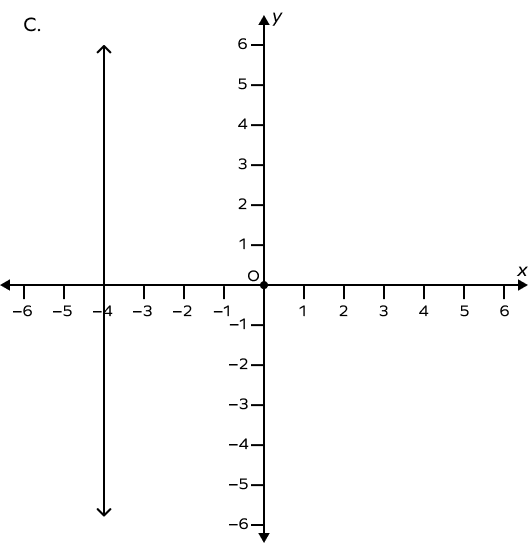
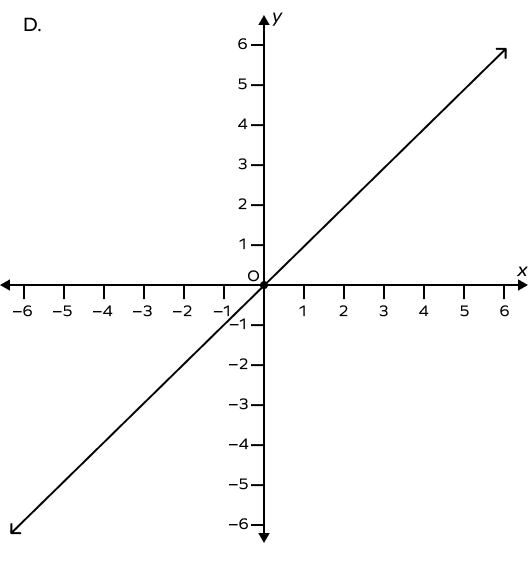
D is the graph that has a line that passes through the origin, i.e., if $x=0$ then $y=0$.

Frequently Asked Questions
Why are the coordinates of origin called (0, 0)?
In a Cartesian Plane, the coordinates of origin are (0, 0) because at this point, x=0 and y=0.
Where is the origin in a graph?
On the Cartesian Plane, the origin is the point of intersection of horizontal and vertical axes. Most often, it is placed at the center of the Cartesian Plane.
What is the rule of rotation by 180 about the origin?
The rule for a rotation by 180about the origin is given by $(x,y) → (-x,−y)$.
















