Sphere – Definition with Examples

What is Sphere?

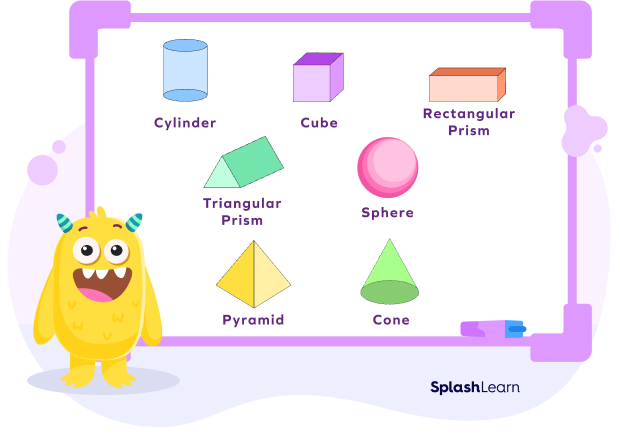
The sphere is a three-dimensional shape, also called the second cousin of a circle. A sphere is round, has no edges, and is a solid shape. The playing ball, balloon, and even light bulbs are examples of sphere shape. 

How Is the Sphere Different From Other Three-Dimensional Objects?

Unlike other three-dimensional objects, such as the cube, cone, and cylinder, the sphere shape does not have any flat surface, vertex, or edge. It only has a rolling surface.

Important Elements of a Sphere Shape

 The important elements of a sphere are the following:

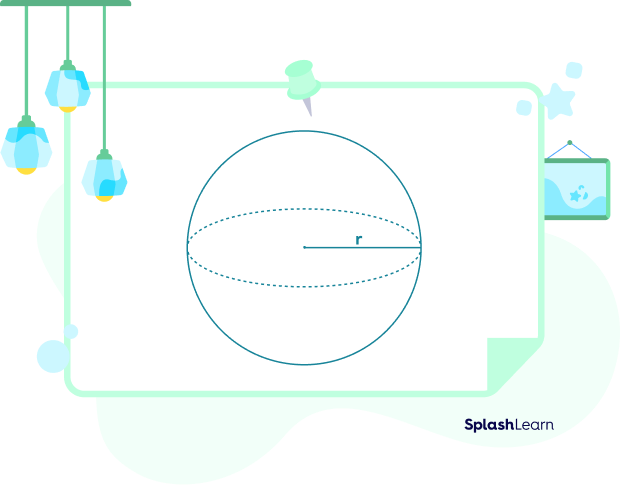
• Radius: The distance between the center of a sphere and its surface is called the radius. It is denoted by the letter r.

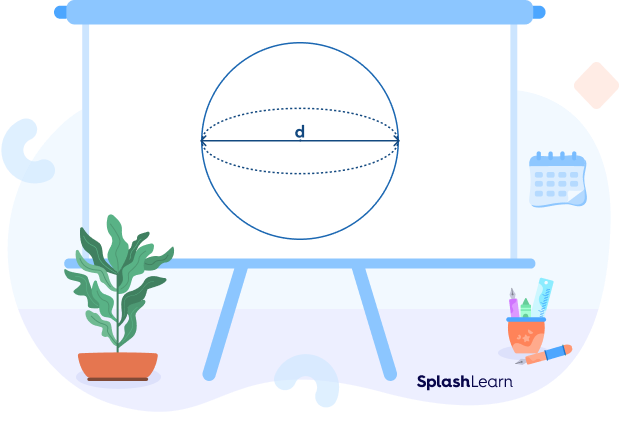
Diameter: Think of the diameter as the longest straight line you can put inside a sphere. The diameter passes through the center and joins two opposite points on the surface of a sphere. Its value is always twice that of the radius. It is denoted by the letter d. The formula to calculate the diameter of a sphere is 2r. 

d $=$ 2r

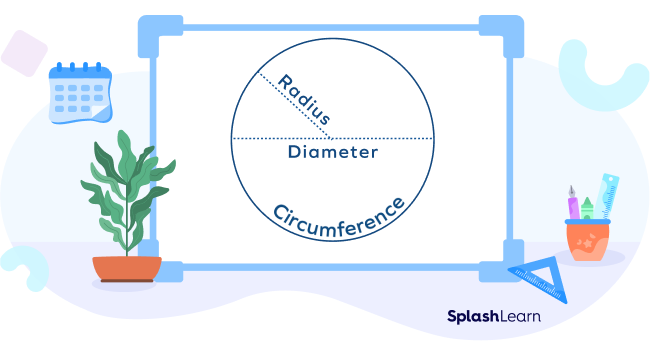
Circumference: The circumference of a sphere can be defined as the greatest cross-section of a circle that we can cut from a sphere. The formula for the circumference of a sphere is given by 2 $\times$ π $\times$ r.

C$=$ 2 π r, where r is the radius of the circle and π (pi) is approximately 3.14.

Did you know that the equator is one of Earth’s great circles? If you were to cut into the Earth right on its equator, you’d have two halves: the northern and southern hemispheres.

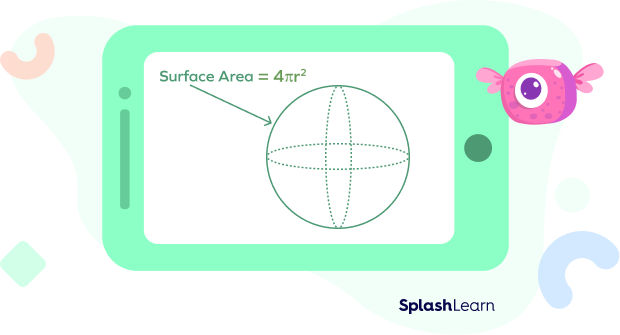
Surface Area: The surface area of a sphere is the total area of its rolling surface. The formula to calculate the surface area of a sphere is given by,

SA $=$ 4 r2 , where r is the radius of the circle and π(pi) is approximately 3.14.

It is measured in square units.

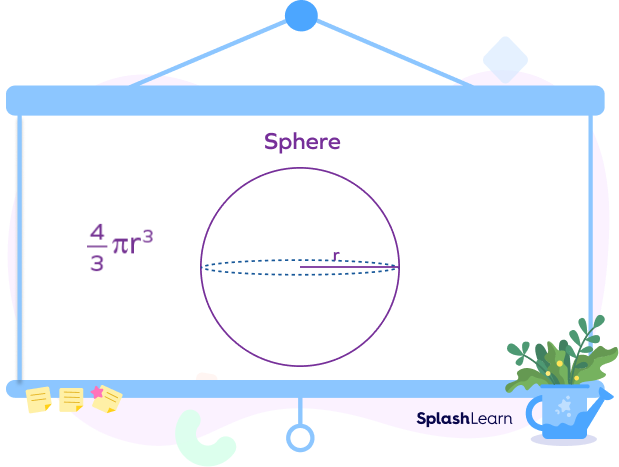
Volume: The volume of a sphere can be defined as the capacity of a liquid that the sphere would hold if it were completely hollow. For example, the amount of water you can fill in an earthen pot defines its volume as a spherical object. The formula to calculate the volume of a sphere is given by,

V $=  \frac{4}{3} r^3$. It is measured in cubic units.

Solved Examples

Example 1: If the radius of a sphere is 5 cm, find its circumference.

Solution:

We know that the circumference of a sphere is given by 

C $= 2 \times$ π $\times$ r.

For the given sphere, r $= 5$ cm.

Therefore, circumference of the given sphere $= 2 \times 3.14 \times 5 = 31.4$ cm.

Example 2: If the radius of a sphere is 10 cm, find its surface area.

Solution:

We know that the surface area of a sphere is given by 

Surface Area $= 4$ r2

For the given sphere, r $= 10$ cm.

Substituting the value of “r” in the formula, we get,

SA $= 4 \times 3.14 \times 10 \times 10$

SA $= 4 \times 3.14 \times 100$

SA $= 1256$ cm² 

Therefore, the surface area of this sphere is $1256$ cm².

Example 3: What is the volume of a sphere of radius 7 cm?

Solution:

We know that the volume of a sphere is given by

V $=  43$ r3

For the given sphere, r $= 7$ cm

V $= 43 \times 3.14 \times 7 \times 7 \times 7$

V $= 43 \times 3.14 \times 343$

V $= 1436.02$ cm³ Therefore, the volume of the given sphere is $1436.02$ cm³

Practice Problems

Frequently Asked Questions