Heptagon – Definition with Examples

What is a Heptagon?

A heptagon is a two-dimensional shape with 7 sides and 7 angles. It belongs to the class of polygons in two-dimensional geometry. Polygons are closed shapes made up of straight lines and no curves.

“Hepta” means seven and “gonia” means angle in the Greek language. By combining these two words, the word “heptagon” is formed, meaning a shape with seven angles. In Latin, this polygon is known as septagon, where “septa” means seven and “gon” means angle. 

Properties of Heptagon

1. It has seven sides, seven angles, and seven vertices.
2. Sum of interior angles of a heptagon is 900°.

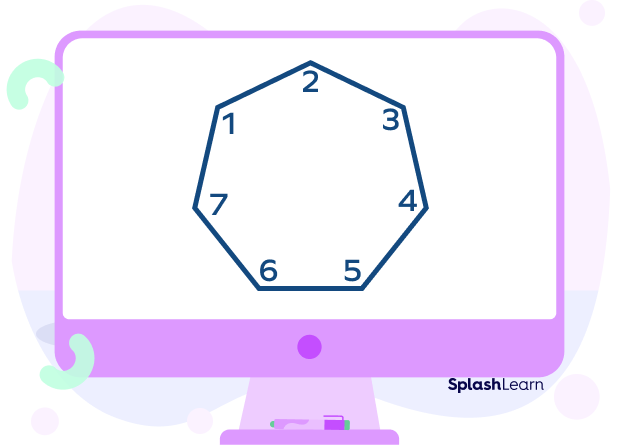
$⦣1 + ⦣2+ ⦣3+ ⦣4+ ⦣5+ ⦣6+ ⦣7 = 900°$

3. It has 14 diagonals.

Types of Heptagon

There are two types of heptagons based on their shapes. They can be seen below. 

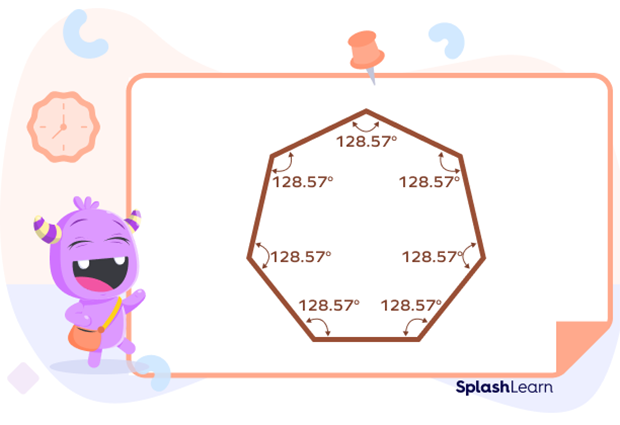
1. Regular Heptagon: It has equal sides and equal angles. Its all the angles are 128.57°, and all the sides are of the same length. There are no parallel sides. 

Properties of a Regular Heptagon

1. The sum of its exterior angles is 360°.
2. The measure of each interior angle is approximately 128.57°.

4. The central angle of a regular heptagon measures about 51.43°.

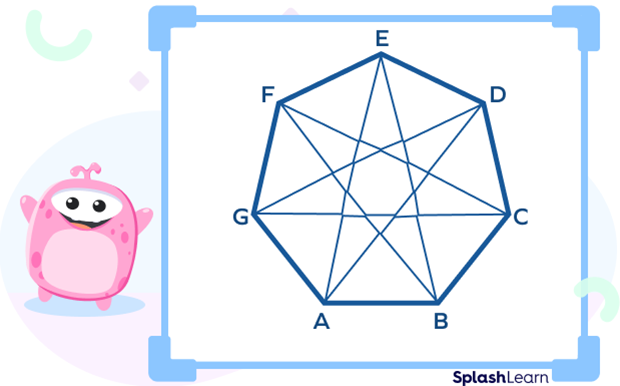
5. A regular heptagon has 14 diagonals.

2. Irregular Heptagon: All its sides and angles vary in length and degree respectively. It can have two or more pairs of parallel sides. 

For example, look at the given image of the coin and the arrow.

Both the objects have 7 sides and are closed, and therefore, heptagonal in shape. However, the coin is in the shape of a regular heptagon, with all sides and angles equal to each other, and the arrow is an irregular heptagon with sides of different lengths and different angles.

So, don’t be confused when you see such an image, because this is as much a heptagon as the image below!

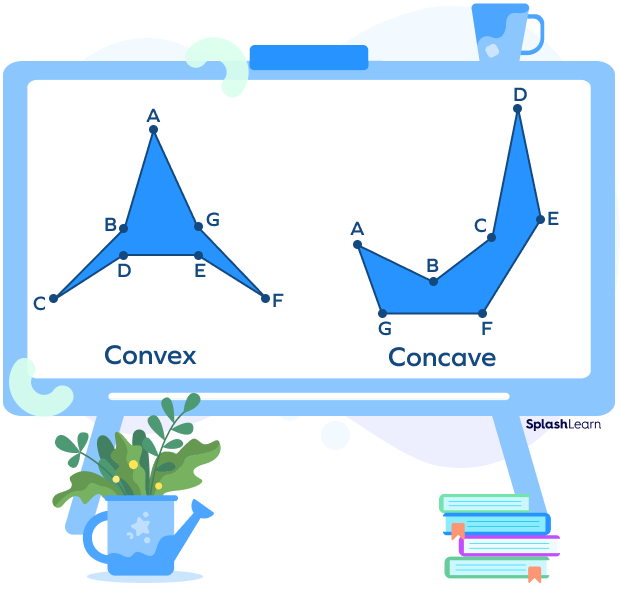
Concave and Convex Heptagon

There are two other types of heptagons as can be seen below. 

1. Concave heptagon: At least one of its angles is pointing inwards, while all the other angles are pointing outwards. Also, one or more interior angles of a concave heptagon are more than 180°.
2. Convex heptagon: All the interior angles are less than 180°, and they seem to be pointing outwards. A regular heptagon is always convex. 

Perimeter of a Heptagon

The perimeter of a shape means the total length of its boundary. For a polygon, the perimeter is given by given by
Perimeter $=$ sum of all sides

Let’s say we have a regular heptagon with each side measuring “a” unit,
The perimeter will be given by the formula,

Perimeter $= a + a + a + a + a + a + a = 7 \times$ a units.

Real-life Examples

In real life, though we may not always notice them, there are multiple examples of heptagons. Some of them are mentioned below.

1.  A cactus: If we see certain cacti from the top, they make up heptagons.

2.  A greenhouse: If you look at the front of a greenhouse, you may notice that it has seven sides and seven angles, and thus is a heptagon.

Solved Examples

1. Find out the perimeter of a regular heptagon with a side of 15 cm. 

Solution: We know that the perimeter of a regular heptagon of side length a is given by,

Perimeter $= 7 \times$ a,

For the given heptagon, a $= 15$ cm,

Therefore, perimeter $= 7 \times 15 = 105$ cm

2. Find the perimeter of an irregular heptagon with sides measuring 7 cm, 8 cm, 9 cm, 10 cm, 11 cm, 12 cm, and 13 cm.

Solution: Perimeter is given by,

Perimeter $=$ Sum of all sides

Therefore, the perimeter of given irregular heptagon $= 7 \text{cm} + 8 \text{cm} + 9 \text{cm} + 10 \text{cm} + 11 \text{cm} + 12 \text{cm} + 13 \text{cm} = 70 \text{cm}$

3. What is the side of a regular heptagon with a perimeter of 224 cm?

Solution: We know that the perimeter of a regular heptagon of side length a is given by,

Perimeter $= 7 \times$ a,

It is given that, Perimeter $= 224$ cm

Therefore, Perimeter $= 7 \times \text{a} = 224$ cm

a $= 2247$

a $= 32 $cm

Practice Problems

Frequently Asked Questions