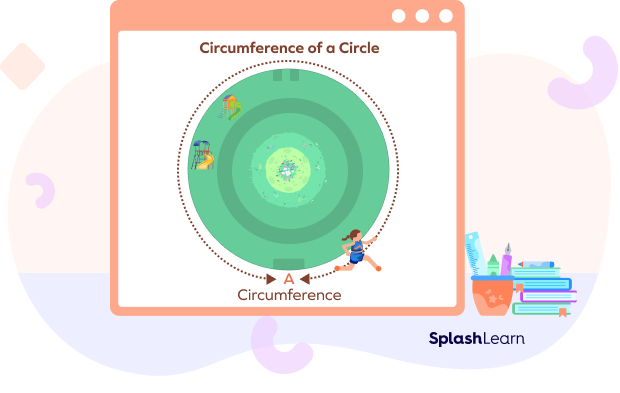
What is the Circumference of a Circle?
We see many circular objects daily, such as coins, buttons, wall clocks, wheels, etc. The boundary of any circular object has great significance in math.

Let’s learn the meaning of circumference of a circle using a real-life example. Suppose a boy walks around a circular park and completes one round. The distance covered by him is the circumference of the circular park.
Recommended Games
Circumference of a Circle: Definition
The circumference is the length of the boundary of a circle. It is also known as the “perimeter” of a circle. Since it represents length, it is measured in units of lengths such as feet, inches, centimeters, meters, miles, or kilometers.
If we cut open a circle and make a straight line, the length of the line would give us the circle’s circumference.
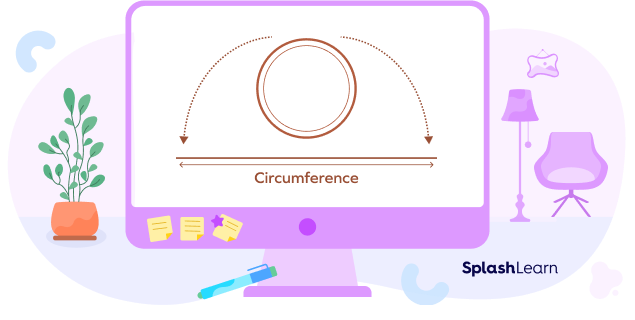
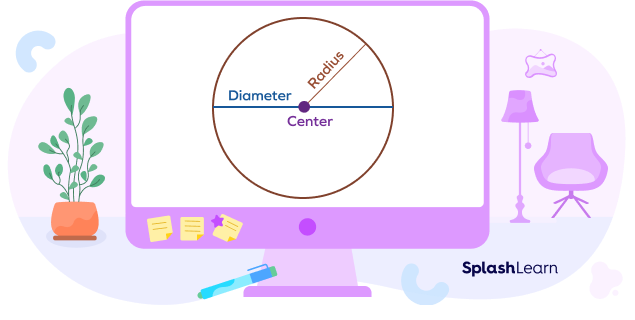
Let’s revise a few important terms related to circles to understand how to calculate the circumference of a circle.
Recommended Worksheets
Diameter of the Circle
The diameter is a straight line passing through the center that cuts the circle in half. Both its endpoints lie on the circumference of the circle.
Radius of the Circle
All points on the boundary of a circle are at an equal distance from its center. The radius is the distance from the center of the circle to any point on the circumference of the circle. It is half the length of the diameter.
How to Find the Circumference of a Circle Using a Thread?
Generally, the outer length of polygons (square, triangle, rectangle, etc.) can be calculated using a scale or ruler, but the same cannot be done for circles because of their curved shape.

Then how can we find the circumference of a circle or how to find the perimeter of a circle? One way is to use a thread. Note that calculating the perimeter of a circle is the same as calculating its circumference.
Step 1: Take a thread and revolve it around the circular object you want to measure.
Step 2: Mark the initial and final point on the thread.
Step 3: Measure the length of the thread from the initial to the final point using a ruler. That would give you the circumference of the circle.
While this method gives us only an estimate, we need to use the circumference formula for more accurate results. The same is discussed in the next section.
What is the Circumference to Diameter Ratio?
The ratio of the circumference to the diameter of any circle is a constant. The constant value is called pi (denoted by π). Let C be the circumference of a circle, and let d be its diameter. Then,
C/d $=$ π
For all circles, regardless of small or big, this ratio remains constant. The approximate value of π is 3.14 or 227.
Formula for the Circumference of a Circle
We just learned that:
Circumference (C) / Diameter (d) $= 3.14159$
Or,
C/d $=$ π
If we shift the diameter to the other side, we get:
C $=$ πd … circumference of a circle using diameter
This gives us the formula for the circumference of a circle when the diameter is given.
Also, we know that the diameter of the circle is twice the radius
or, d $= 2$r
So, replacing the value of d in the above formula, we get:
C $=$ π(2r)
or C $= 2$πr … circumference of a circle using radius
Therefore, the circumference circle equation is C $= 2$πr.
Example 1: If the radius of a circle is 7 units, then the circumference of the circle will be
$2 \times$ π $\times 7 = 2 \times 3.14159 \times 7$
$= 43.98$ units
Example 2: Suppose that the diameter of the circle is 12 feet. Then, we can use the formula πd to calculate the circumference.
Circumference $=$ πd $= 3.14159 \times 12 = 37.69$ feet
Conclusion
Now you know how to calculate the circumference of a circle if you know its radius or diameter!
Since the circumference gives the length of the circle’s boundary, it serves many practical purposes. Solving the practical problems given will help you better grasp the concept of the circumference of the circle. Good luck!
Solved Examples
1. What is the circumference of a circle with a diameter of 14 feet? Use π $= 3.14$.
Solution:
Given, diameter (d) = 14 feet
Circumference of the circle = πd
= 3.14 × 14 feet
= 43.96 feet
2. The radius of a circle is 6 inches. What is the circumference of the circle? Use π = 3.14.
Solution
Given, radius (r)$= 6$ inches
Circumference (c)$= 2$πr
$= 2 \times 3.14 \times 6$ inches
$= 37.68$ inches
3. The circumference of a circle is 100 feet. Find its diameter. Use π $= 3.14$.
Solution:
Applying the formula:
Circumference (C)$=$ πd
100 feet $= 3.14 \times$ d
d $= 100$ feet / 3.14
d $= 31.85$ feet
Therefore, d $= 31.85$ feet
4. The circumference of a circle is 120 m. Find its radius. Use π $= 3.14$.
Solution:
We know that
Circumference (C) $= 2$πr
$120 =$ 2πr
$1202 = 3.14 \times$ r
$60 = 3.14 \times$ r
r $= 603.14$
Therefore, r $= 19.11$ m
5. If the diameter of a circle is 15 miles, what will be the length of its boundary?
Solution:
The length of the boundary of a circle is the circle’s circumference.
Hence, let’s find the circumference first.
Given, diameter (d) $= 15$ cm
Circumference (C) $=$ πd $= 3.14 \times 15$ cm $= 47.1$ cm
Practice Problems
Circumference of a Circle
The perimeter of a square wire is 25 inches. The same wire is bent to form a circle. Find the radius of the circle thus formed.
The perimeter of the square = total length of the wire $=$ circumference of the circle.
Hence, the circumference of the circle (C) $=$ 25 inches.
Applying the formula:
C $=$ $2πr$
25 inches $= 2 \times 3.14 \times$ r
25 inches $= 6.28 \times$ r
r $= 25/6.28$
r $= 3.98$ inches
The diameter of a cycle wheel is 7 inches. How many times must the wheel rotate to cover a distance of 110 feet? Take π $=\frac{22}{7}$
The circumference of the wheel will give us the distance covered by the wheel in one rotation. So, let us calculate the circumference first.
Given, diameter (d) $=$ 7 inches
Circumference $=$ πd
$= 22/7 \times 7$
$= 22$ inches
So, the distance covered by the wheel in one rotation $= 22$ inches
Total distance to be covered $= 110$ feet $= (110 \times 12)$ inches $= 1320$ inches
Hence, no. of rotations required$= 1320/22 = 60$
A circular flowerbed has a diameter of 20 feet. Find the cost of fencing the flowerbed at the rate of $10$ per feet. Take $\pi$ = 3.14.
Diameter of the flowerbed (d) $=$ 20 feet
Fencing the circular flowerbed refers to the boundary of the circle, i.e., the circumference of the circle.
Circumference of the flowerbed $=$ πd
$= 3.14 \times 20$ m $= 62.8$ feet
Now, the cost of fencing $=$ $\$$10 per ft
So, the cost of fencing $62.8$ feet $= 62.8 \times$ $\$$10 $=$ $\$$628
The difference between a circle's circumference and diameter is 10 feet. Find its radius. Take π $= 3.14$.
Given: Circumference – Diameter $=$ 10 feet
We know that:
Circumference $= 2$πr
Diameter $= 2$r
So, $2$πr $-$ $2$r $= 10$ feet
$2$r$(\text{π}$ $-$ $1) = 10$ feet
$2$r $(3.14$ $-$ $1) = 10$ feet
$2$r $\times 2.14 = 10$ feet
r = 10 / 4.28
r = 2.33 feet
The ratio of the circumference of two circles is 4:5. Find the ratio of their radius.
We know that the circumference of a circle is $2$πr.
Let us consider the radius of the first circle to be R₁ and that of the second circle to be R₂.
So, Circumference of 1st circle $= 2$πR₁
Circumference of 1st circle $= 2$πR₂
Ratio $= \frac{2πR_1}{2πR_2} = \frac{4}{5}$
Canceling $2$π from both the ratios,
$\frac{R_1}{R_2}= \frac{4}{5}$
Therefore, the ratio of the two radii is 4:5.
Frequently Asked Questions
What is the difference between a sphere and a circle?
A circle is a two-dimensional figure, whereas a sphere is a three-dimensional solid object. Hence, a circle does not have a volume, but a sphere does.
What is the circumference of Earth?
The circumference of the earth is about 24,901 miles.
What is the area of a circle?
The area of the circle is the space occupied by the boundary of the circle. It is given by
What is the formula to calculate the circumference of a semicircle?
The circumference of a semi-circle can be calculated as C $=$ πr $+$ d.
What is the difference between the circumference and area of a circle?
The circumference is the length of the outer boundary of a circle, while the area is the total space enclosed by the boundary.
Related Articles Link