What Is a Degree Measure of an Angle?
A degree is a unit of measurement that helps measure the magnitude of an angle.
In geometry, the two common units of measurement of angles — degree and radian. However, degrees is the most commonly used and the most familiar unit for measuring angles.
What Are Angles?
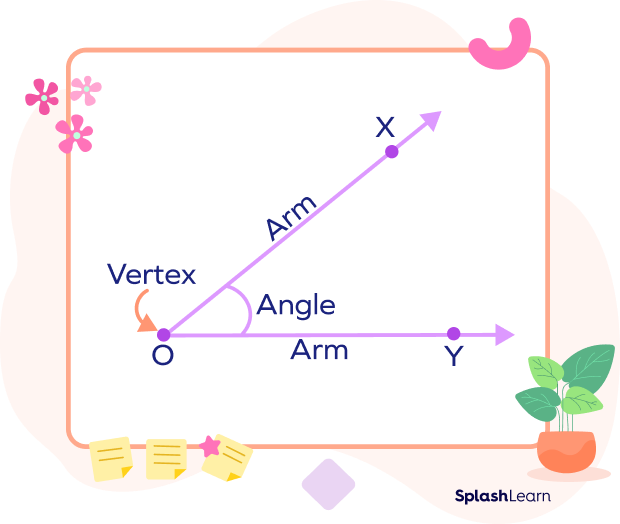
An angle is a geometric figure formed when two rays meet at the common point called vertex. It is denoted by the symbol ∠.
Example: In the given diagram shown an angle XOY, denoted by ∠XOY.
The point O is the vertex. Rays OX and OY are arms. OY is the initial arm and OX is the terminal arm.
The measure of an angle is the amount of rotation of the terminal arm from the initial arm.
Recommended Games
Degree: Definition
The degree is a unit of angular measurement used to quantify the size or magnitude of an angle. It is a measure of how much one line or ray deviates from another. A full rotation (a circle) represents 360 degrees.
Recommended Worksheets
Degree Symbol in Math
An angle in degrees is denoted by a tiny circle (°) that is often placed in the superscript position after the number (at the top-right corner of a number).
For example, 40 degrees = 40°
Note that this symbol is to be used after the numerical value representing the measurement of an angle (angle measure), and not after the name of an angle.
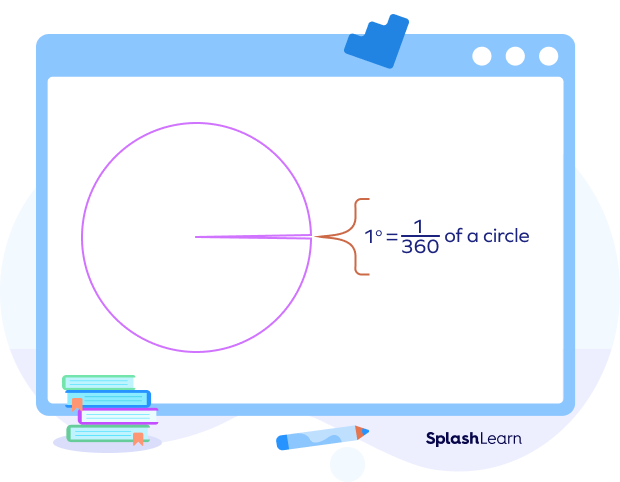
What Is One Degree?
An angle measuring 1 degree, denoted as 1°, is equal to $\frac{1}{360}$ of one full rotation.
One full rotation is equivalent to 360°. Thus, a circle represents an angle of 360 degrees at the center.
What Is a Protractor?
In geometry, we can easily measure an angle in degrees with the help of a protractor.
A regular protractor shows degree markings from 0° to 180°, as shown below.
A protractor has two scales — inner scale and outer scale.
The outer scale starts from 0° and goes up to 180° in a clockwise direction.
The inner scale has the same range of 0° to 180° in the counterclockwise direction.

Full circle protractors are also available which show angles all the way up to 360 degrees.
How to Measure Angles in Degrees Using a Protractor
Let’s understand how to measure angles in degrees with the help of an example.
Step 1: We place the protractor in such a way that its center is aligned with the vertex of the angle. We also precisely align the baseline of the protractor with the initial arm of the angle.
Step 2: Start the measurement from the 0° marking at the bottom-right corner. Use the internal markings on the protractor’s arc to calculate the angle. Note down the inner scale marking that aligns with the terminal arm of the angle.
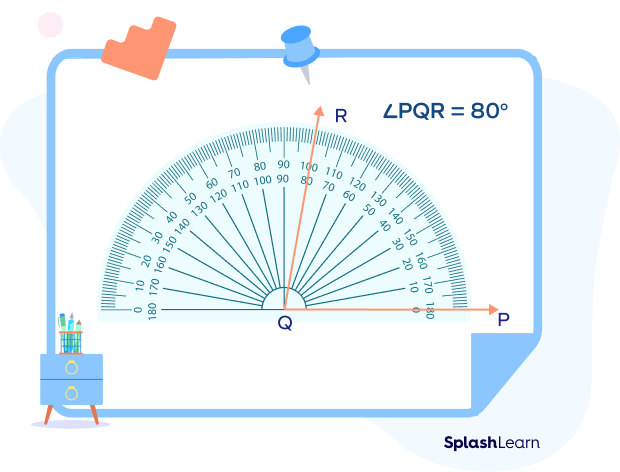
Example: In the given diagram, the vertex Q is aligned to the center of the protractor. The initial arm QP is aligned with the baseline of the protractor.
m∠PQR = 80°
What Are Different Types of Angles Based on Measurement in Degrees?
We can classify angles based on the angle measurements in degrees. Here’s a chart representing different types of angles:
| Type | Definition | Diagram |
|---|---|---|
| Acute Angle | An angle whose measure is less than 90° is called an “Acute” angle. Examples: 50°, 81°, etc. | 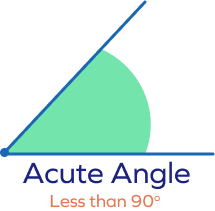 |
| Right Angle | An angle that is exactly 90° in measurement is called a “Right” angle. | 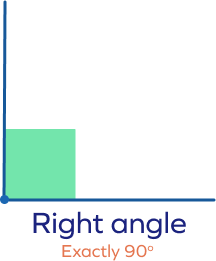 |
| Obtuse Angle | An angle that is greater than 90° and less than 180° is called an “Obtuse” angle. Examples: 110°, 171°, etc. |  |
| Straight Angle | An angle that is exactly 180° in measurement is called a “Straight” angle. Its two arms form a straight line. |  |
| Reflex Angle | An angle that is greater than 180° and less than 360° is called a “Reflex” angle.Examples: 200°, 312°, etc. |  |
| Complete Angle (Full Angle) | An angle that is exactly 360° in measure is called a “Complete” angle or a “Full” angle. It represents a complete circle or a full turn. |  |
What Are Special Angles in Degrees?
Special angles refer to those angles that are used frequently in geometry because of their special measurements.
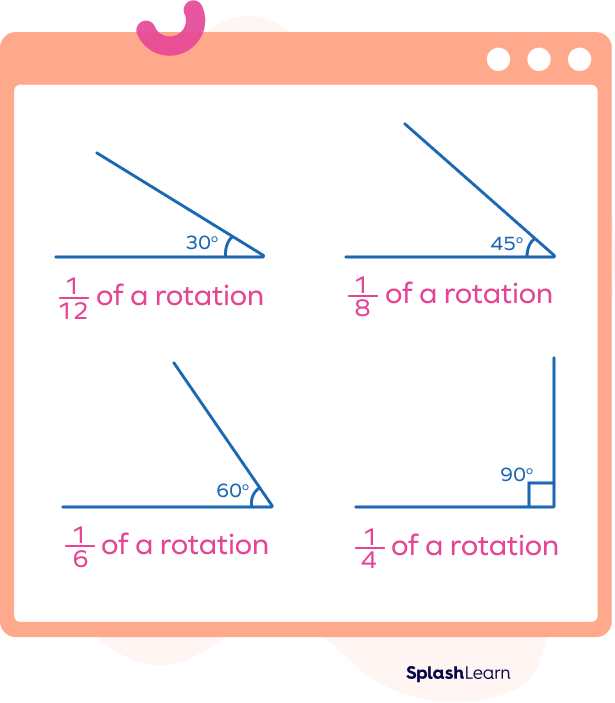
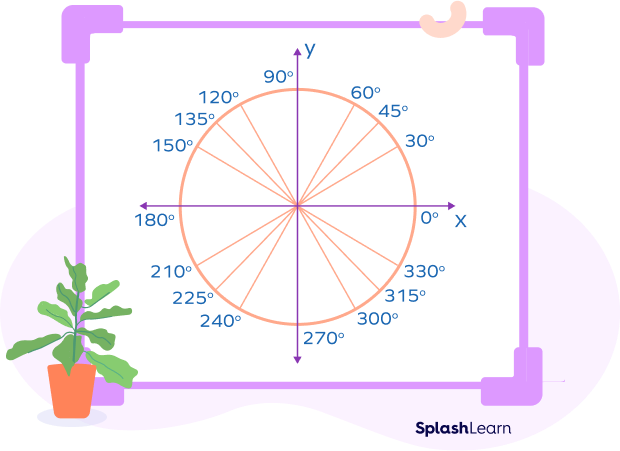
Here’s how we can represent these angles in the standard position (vertex is located at the origin, and its initial side extends along the positive x-axis).
Relationship Between Degrees and Radians
Besides degrees, radians are another unit of measurement of angles.
An angle of one radian is made by an arc at the center if arc-length is equal to the radius.
One radian is approximately equal to 57.2958 degrees. 2π radians represent a full counterclockwise rotation.
- To convert radians into degrees, we use the following formula:
Angle in degrees = Angle in radians $\times \frac{180^{\circ}}{\pi}$
- To convert degrees into radians, we use the following formula:
Angle in radians = Angle in degrees $\times \frac{\pi}{180^{\circ}}$
| Angle in Degrees | Angle in Radians |
|---|---|
| 30° | $\frac{\pi}{6}$ |
| 45° | $\frac{\pi}{4}$ |
| 60° | $\frac{\pi}{3}$ |
| 90° | $\frac{\pi}{2}$ |
| 180° | $\pi$ |
| 360° | $2\pi$ |
Facts about Degree Angle Measure
- The measure of an angle is the amount of rotation of the terminal arm from the initial arm. If the rotation is clockwise, the measure is taken to be negative. If the rotation is anti-clockwise, the angle measure is taken to be positive.
- If the sum of two angles is 90 degrees, the angles are called complementary angles.
- If the sum of two angles is 180 degrees, the angles are called supplementary angles.
- The sum of three angles in a triangle is always 180 degrees.
Conclusion
In this article, we learned about the degree unit of measuring angles along with its definition and symbol. We also discussed how to measure angle in degrees using a protractor. Let’s solve a few examples and practice MCQs for better comprehension.
Solved Examples on Degree Angle Measure
1. Convert into radians.
i) 4 degree angle
ii) 5 degree angle
Solution:
i) Angle in radians = Angle in degrees $\times \frac{\pi}{180^{\circ}}$
Angle in radians $= 4^{\circ} \times \frac{\pi}{180^{\circ}}$
Angle in radians $= \frac{\pi}{45}$
ii) Angle in radians = Angle in degrees $\times \frac{\pi}{180^{\circ}}$
Angle in radians $= 5^{\circ} \times \frac{\pi}{180^{\circ}}$
Angle in radians $= \frac{\pi}{36}$
2. Classify given angles in degrees as acute, obtuse, right, reflex, straight, or complete.
i) $90^{\circ}$
ii) $185^{\circ}$
iii) $29^{\circ}$
iv) $225^{\circ}$
Solution:
i) $90^{\circ}$: Right angle
ii) $185^{\circ}$: A reflex angle since it lies between $180^{\circ}$ and $360^{\circ}$
iii) $29^{\circ}$: An acute angle since it is less than $90^{\circ}$
iv) $225^{\circ}$: A reflex angle since it lies between $180^{\circ}$ and $360^{\circ}$
3. What is the type of angle made if you add 2 straight angles?
Solution:
1 straight angle $= 180^{\circ}$
2 straight angles $= 2 \times 180^{\circ} = 360^{\circ}$
A $360^{\circ}$ is called a complete angle or a full angle.
4. If you divide a circle into four equal parts, what is the type of angle made by each piece at the center?
Solution:
A circle represents a $360^{\circ}$ angle at the center.
If you divide a circle into four equal parts (quarters), each quarter will represent a $\frac{360^{\circ}}{4} = 90^{\circ}$ angle at the center.
Practice Problems on Degrees
Degrees (Angle) – Definition, Symbol, Conversion, Examples, Facts
The sum of 3 straight angles is
1 straight angle $= 180^{\circ}$.
3 straight angles $= 3 \times 180^{\circ} = 540^{\circ}$.
Find the correct option.
1 degree is equal to 1/360 of a complete revolution.
What angle in degrees does ∠AOB represent on the protractor?
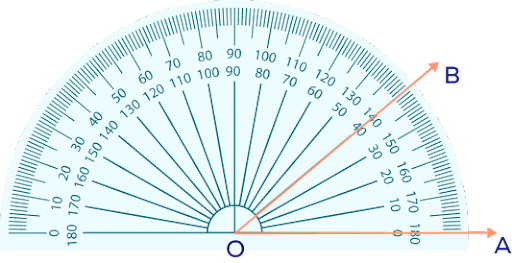
By looking at the internal markings on the protractor's arc, it is clear that m∠AOB $= 40^{\circ}$.
Convert $\frac{5\pi}{4}$ radians into degrees.
$\frac{5\pi}{4} = \frac{5\pi}{4} \times 180^{\circ} = 5 \times 45^{\circ} = 225^{\circ}$.
Find the incorrect option.
1 right angle $= 90^{\circ}$
2 right angles $= 2 \times 90^{\circ} = 180^{\circ}$
4 right angles $= 4 \times 90^{\circ} = 360^{\circ}$
6 right angles $= 6 \times 90^{\circ} = 540^{\circ}$
8 right angles $= 8 \times 90^{\circ} = 720^{\circ}$
Frequently Asked Questions about Degree Angle Measure
What is the value of a full turn in degrees?
The value of a full turn in degrees is 360°.
Is 1 degree greater than 1 radian?
1 radian is approximately equal to 57.2958 degrees. Thus, 1 radian is much greater than 1 degree.
What is 1 radian?
One radian is defined as the angle subtended by an arc at the center of a circle whose arc-length is equal to the radius of the circle.
How many degrees does a straight line form?
A straight line always forms 180 degrees.




































