What Is a 360 Degree Angle?
A 360 degree angle is a complete angle or a full angle. It represents a complete or full rotation and represents a circle at a given point. In simple words, a circle has an angle of 360 degrees around the center. To form a 360 degree angle, the initial arm takes a full rotation and comes back to its original position.
360 degree angle names: Complete Angle, Full Angle, Perigon
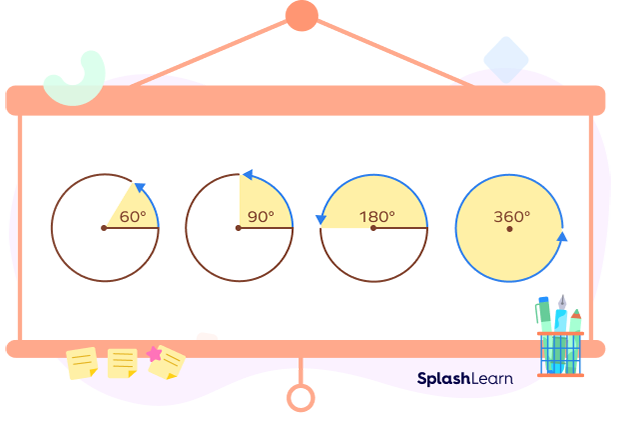
A 360 degree angle is
- six times a $60^{\circ}$ angle.
- four times a right angle ($90^{\circ}$ angle).
- two times a straight angle ($180^{\circ}$ angle).
Recommended Games
Definition of a 360 Degree Angle
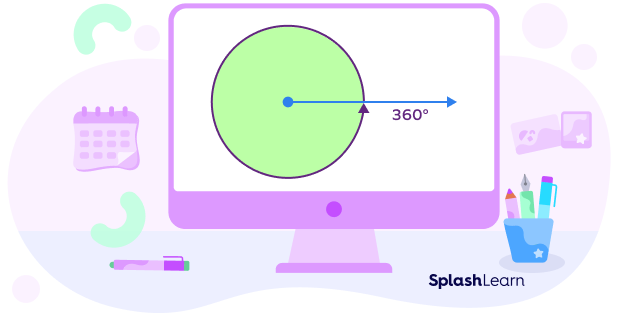
A 360 degree angle is a complete angle. It is an interior angle measure of a circle all the way around its center as it forms a circle around a point. In radians, a 360 degree angle is equivalent to $2\pi$ radians.
If you rotate a ray completely (counterclockwise) to reach its initial position, it forms a 360 degree angle.
Recommended Worksheets
How to Draw a 360 Degree Angle
There are two simple ways to draw a 360 degree angle. You can use a compass or a protractor for this. Take a look at the step-by-step guide to draw this.
Constructing a 360 Degree Angle Using a Compass
Step 1: First, place the tip of the compass at any fixed point.
Step 2: Widen the other end at a suitable length.
Step 3: Keeping the tip of the compass stable at the point and keeping this fixed length, start rotating the pencil.
Step 4: Rotate the pencil till you reach the same point from where you began. You will have a 360 degree angle.

Constructing a 360 Degree Angle Using a Protractor (bold)
To construct a 360 degree angle with a protractor, get a 360 degree protractor that is round in shape. This protractor will have a center and you only have to trace along the circumference of the round protractor to make a 360 degree angle. Refer to the image provided below to understand this better.

Difference Between a 360 Degree Angle and a Zero Angle

One might get confused between the zero angle and the complete angle because of the similarity in the appearance. However, in case of the zero angle, there is no rotation involved. When the complete angle is formed, a complete rotation or a full turn is involved.
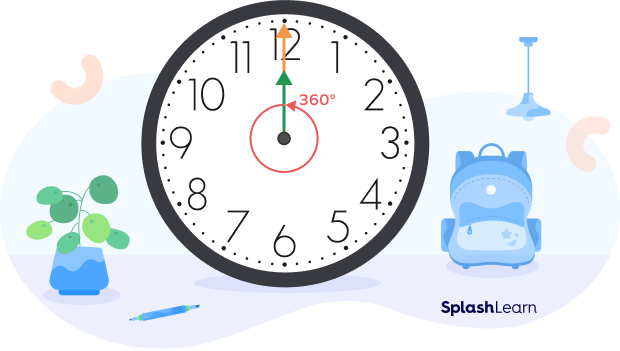
Real-life Example
In an analog clock, the angle covered by the hour hand in 12 hours is 360 degrees. Similarly, a minute hand produces a 360 degree angle in one hour.
Facts about 360 Degree Angle
- A 360 degree angle is also known as a complete angle or a full angle or a perigon.
- A full angle measures $2\pi$ radians.
- A 360 degree angle is four times a right angle (90 degrees).
- A pair of angles whose sum is 360 degrees are called “conjugate angles.”
Conclusion
In this article, we learned about the 360 degree angle. It is also called a complete angle, full angle and full turn. Let’s solve a few examples of the topic to understand it better!
Solved Examples on 360 Degree Angle
1. How many straight angles will make a complete angle?
Solution:
A straight angle is 180 degrees.
A complete angle is 360 degrees.
As 180 + 180 = 360, two straight angles will make a complete angle.
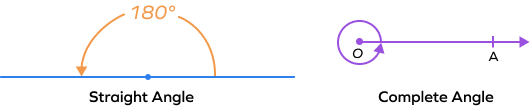
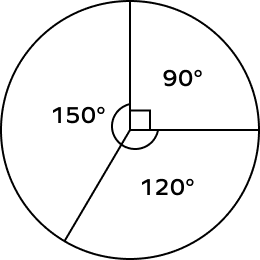
2. Three central angles X, Y, and Z form a circle such that m$\angle X = 90^{\circ}$, $\angle Y = 120^{\circ}$. What is m$\angle\text{Z}$?
Solution:
We know that the angle formed at the center of a circle is 360 degrees.
m$\angle X + m\;\angle Y + m\;\angle Z = 360^{\circ}$
$90^{\circ} + 120^{\circ} + m\; \angle Z = 360^{\circ}$
$m\; \angle Z = 360^{\circ} \;-\; (90^{\circ} + 120^{\circ})$
$m\; \angle Z = 150^{\circ}$
3. Find the value of $\angle x$ in the following diagram.
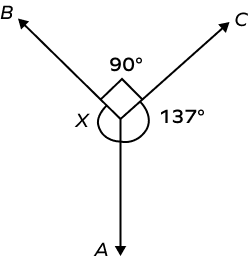
Solution:
The three angles together make a complete angle.
$137^{\circ} + 90^{\circ} + m\; \angle x = 360^{\circ}$
$m\; angle\; x = 360^{\circ} \;–\; 227^{\circ}$
$m\; \angle\; x = 133^{\circ}$
Practice Problems on 360 Degree Angle
360 Degree Angle: Definition, Construction, Examples, FAQs
How many $5^{\circ}$ angles make a complete angle?
To find how many $5^{\circ}$ angles make a complete angle we will divide $360^{\circ}$ by $5^{\circ}$.
$\frac{360^{\circ}}{5^{\circ}} = 72$
$72 \times 5^{\circ} = 360^{\circ}$
The sum of all angles around a point equals
The sum of all angles around a point equals $360^{\circ}$.
Find the value of $x$ if $(x+ 125)^{\circ}$ and $(x + 150)^{\circ}$ add up to $360^{\circ}$.
$(x + 125)^{\circ} + (x + 150)^{\circ} = 360^{\circ}$
$2x = 360^{\circ} \;-\; 275^{\circ}$
$2x = 85^{\circ}$
$x = 42.5^{\circ}$
Which of the following is true about the complete angle?
A complete angle is equal to $2\pi$ radians.
How many right angles make a 360 degree angle?
Four right angles make a 360 degree angle.
$4 90^{\circ} = 360^{\circ}$
Frequently Asked Questions about the 360 Degree Angle
What is a 360 degree angle called?
A 360 degree angle is often referred to as a complete angle or a full angle or a full turn.
360 degree angle names: Full angle, full turn, complete angle.
How can we draw a 360 degree angle with a compass?
Simply draw a line using a ruler and place the pointed head of the compass on one end. Using a suitable radius on the compass, draw a circle around it. Once the circle is complete, you will have a 360 degree angle at the center.
How can we identify a 360 degree angle?
A 360 degree angle looks like a circle as it takes a complete or full turn around a point.
Can we draw a 360 degree angle using a protractor?
Yes. Using a round or a circle-shaped protractor, we can draw a 360 degree angle. If we place the protractor on a flat surface and trace the edges around the protractor, we will have a 360 degree angle in the shape of a circle.





























