What are Common Multiples in Math?
Common multiples are the multiples that are common between a given set of numbers.
Multiplying a number by counting numbers gives us its multiples. In math, the meaning of a multiple is the product or result of one number multiplied by another number.
We all know multiplication tables as we always use them to solve math problems. When we use these tables, we are also using multiples. You see, when we multiply two numbers, the answer is their multiple.
We can write the list of multiplies of a number by multiplying it with natural numbers.
Example: What are the multiples of 4?
To create a list of multiples of 4, we multiply 4 by the numbers 1, 2, 3, and so on as shown below:
$4 \times 1 = 4$
$4 \times 2 = 8$
$4 \times 3 = 12$
$4 \times 4 = 16$
… and so on.
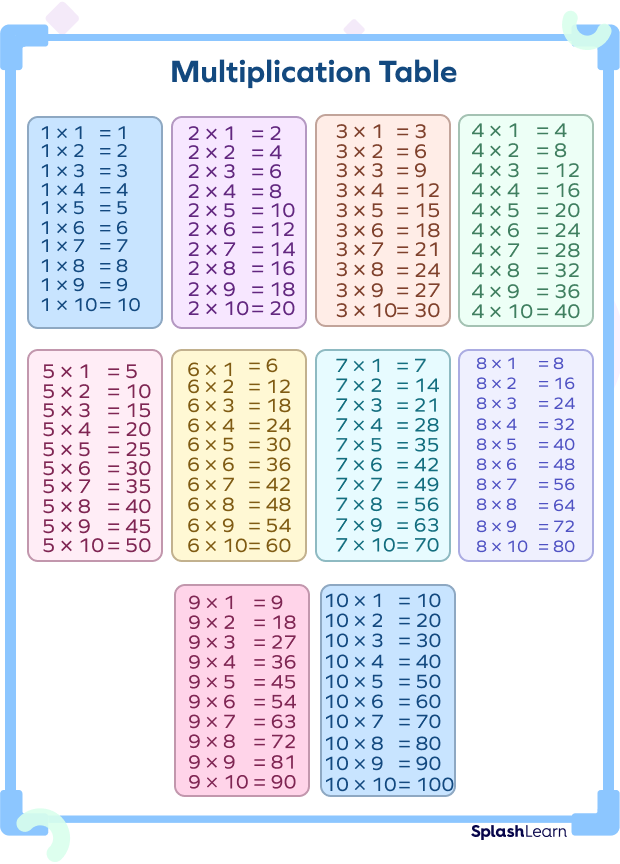
Take a look at the multiplication tables (times tables) which represent the first ten multiples of numbers from 1 to 10.
So, what are common multiples? Let us try and understand with an example. It is quite simple. Let’s find the common multiples of 6 and 7.
First, we can list the multiples of 6 and 7 by multiplying them by numbers 1, 2, 3, …, and so on.


What are the multiples of 6?
The multiples of 6 are: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 79, 84, …
What are the multiples of 7?
The multiples of 7 are: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, …
So, what numbers do you find common in the multiples of 6 and 7?
Common multiples of 6 and 7: 42, 84, …
Recommended Games
Common Multiples Definition
A common multiple is defined as a number which is a shared multiple of a given set of numbers. The multiples common to two or more numbers are called the common multiples of those numbers.
Recommended Worksheets
Common Multiples Between Two Numbers
Finding common multiples between two numbers is very simple. List the multiples (the first few multiples) of both the numbers as we discussed in the previous example. Identify the multiples that appear in both the lists.
Example: Common multiples of 6 and 8
| Multiples of 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | … |
| Multiples of 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | … |
Common multiples of 6 and 8: 24, 48, … and so on.
Common Multiples Between Three Numbers
We can use the Listing method to find the common multiples of three numbers as well. Here, we just need to ensure that the multiples that we identify are present in all the three lists. In simple words, we need to find the numbers that are multiples of all the three numbers.
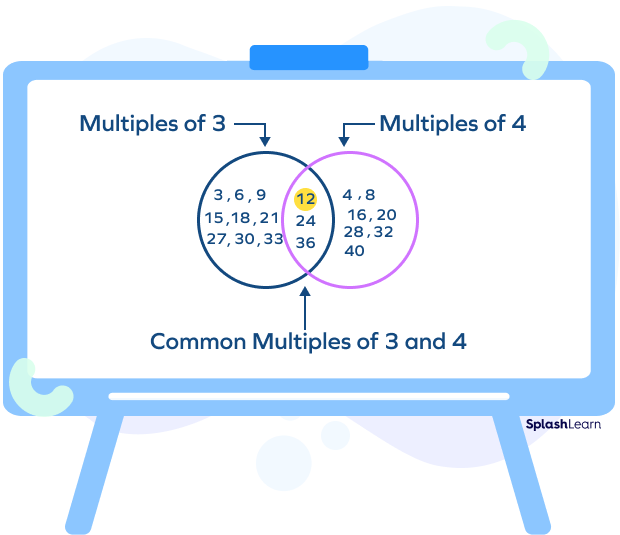
Example: Common multiples of 3, 4, and 6
| Multiples of 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| Multiples of 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| Multiples of 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
Common multiples of 3, 4, and 6: 12, 24, … and so on.
How To Find Common Multiples
We can find the common multiples of two or more numbers by listing the multiples of each number.
To find the common multiples of 6 and 7, let us mark the multiples of 6 and 7 on a hundred grid. We will mark the multiples of 6 by a circle and multiples of 7 by a cross.
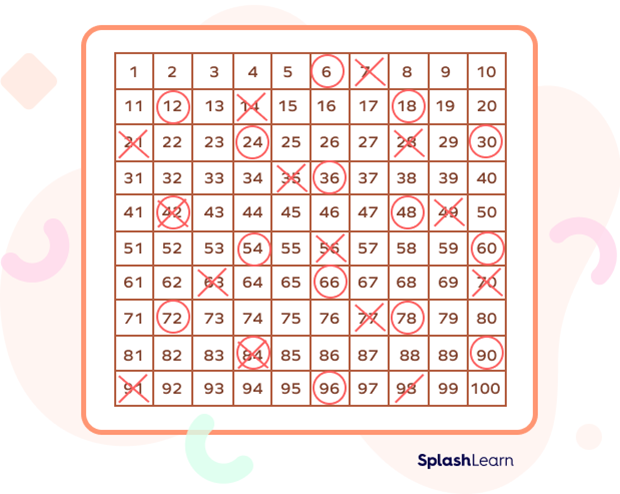
The numbers that are circled as well as crossed are the common multiples of 6 and 7.
So, the common multiples of 6 and 7 are 42 and 84.
Take a look at one more example.
Example: Find common multiples of 4 and 12.
Multiples of 4 = 4, 8, 12, 16, 20, 24, 28, 32, 36, …
Multiples of 12 = 12, 24, 36, 48, 60, 72, …
Common multiples of 4 and 12 = 12, 24, …
What Is a Least Common Multiple?
The smallest common multiple of two or more numbers is called the Least Common Multiple (LCM).
For example, to find the common multiples of 3 and 4, we list their multiples and then find their common multiples.
The multiples of 3 are: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, …
The multiples of 4 are: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, …
The common multiples of 3 and 4 are: 12, 24, 36, ….
The smallest common multiple is 12. So the LCM of 3 and 4 is 12.
Properties of Common Multiples
- A number can have an infinite number of multiples. Therefore, any two numbers or set of numbers can have an infinite number of common multiples.
- For any two numbers a and b, the product $a \times b$ is always a common multiple of a and b.
Example: $6 \times 8 = 48$ is a common multiple of 6 and 8.
- If two numbers a and b are coprime, then their common multiples are the multiples of $(a \times b)$.
Example: 2 and 3 are coprime numbers.
$2 \times 3 = 6$
Common multiples of 2 and $3 = 6, 12, 18, 24, 30$, …
- The LCM of two co-prime numbers is equal to the product of the two numbers.
Example: What is the least common multiple of 3 and 5?
3 and 5 are co-prime numbers.
LCM(3, 5) $= 3 \times 5 = 15$
- If b is the multiple of a, then the LCM of a and b is b.
Example: LCM (5, 10) $= 10$
Solved Examples on Common Multiples
1. What are the multiples of the number 9?
Solution:
We know that we can get multiples of a number by multiplying it by 1, 2, 3, …, and so on.
So, the multiples of 9 are : 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, …
2. Find two common multiples of the numbers 2 and 10.
Solution:
We know that the multiples common to two or more numbers are called the common multiples of those numbers.
Now, the multiples of 2 are: 2, 4, 6, 8, $\underline{10}$, 12, 14, 16, 18, $\underline{20}$, …
and the multiples of 10 are: $\underline{10}$, $\underline{20}$, 30, 40, 50, 60, 70, 80, 90, 100, …
So, the two common multiples of 2 and 10 are 10 and 20.
3. Find the LCM of 3 and 5.
Solution:
The smallest common multiple of two or more numbers is called the Least Common Multiple (LCM).
The multiples of 3 are: 3, 6, 9, 12, $\underline{15}$, 18, 21, 24, 27, $\underline{30}$, …
The multiples of 5 are: 5, 10, $\underline{15}$, 20, 25, $\underline{30}$, 35, 40, 45, 50, …
The common multiples of 3 and 5 are: 15, 30, …
The smallest of these is 15. So the LCM of 3 and 5 is 15.
Practice Problems On Common Multiples
Common Multiples - Definition with Examples
Which of the following is not a multiple of 8?
The multiples of 8 are: 8, 16, 24, 32, 40, …
So, 28 is not a multiple of 8.
Which of the following is a common multiple of 16 and 20?
Multiples of 16 are: 16, 32, 48, 64, $\underline{80}$, 96, 112, 128, 144, $\underline{160}$…..
Multiples of 20 are: 20, 40, 60, $\underline{80}$, 100, 120, 140, $\underline{160}$, 180, 200….
So, the common multiples of 16 and 20 are: 80, 160, and so on.
Which of the following is not a common multiple of 12 and 15?
30 is a multiple of 15, but not of 12. So, 30 is not a common multiple of 12 and 15.
Which of the following is the LCM of 9 and 18?
18 is the smallest common multiple of 9 and 18. So, 18 is the LCM of 9 and 18.
Observe the given numbers. Which number is a multiple of 6?
$6 \times 9 = 54$
54 is a multiple of 6.
Frequently Asked Questions On Common Multiples
What are the multiples of the number zero?
The multiples of zero is zero. Every other whole number has infinitely many multiples.For example: $25 \times 0 = 0$ ; $1.0836 \times 0 = 0$ ; $\frac{-9}{87} \times 0 = 0$.
What are the multiples of the number one?
All the natural numbers are multiples of 1. There is no end to multiples of any number. The first ten multiples of the number 1 starting from 1 are 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10.
What is the LCM of prime numbers?
The short form LCM stands for Least Common Multiple. The smallest common multiple of two or more prime numbers is their product.
For example: The LCM of 3 and 7 is 21.
What are the Common Multiples of 3 and 4?
Common multiples of 3 and 4 are 12, 24, 48, and so on.
What are the Common Multiples of 4 and 6?
Common multiples of 4 and 6 are 12, 24, 36, 48, and so on.
What are the Common Multiples of 10 and 12?
Common multiples of 10 and 12 are 60, 120, 180, 240, and so on.
What are the first two multiples that 5 and 7 have in common?
Common multiples of 5 and 7 are 35, 70, 105, 140, and so on.
The first two common multiples of 5 and 7 are 35 and 70.




































