What are Equivalent Fractions?
Fractions represent equal parts of a whole or a collection. A fraction has two parts. The number on the top of the line is called the numerator which tells how many equal parts of the whole or collection are taken. The number below the line is called the denominator and it shows the total number of equal parts the whole is divided into or the total number of equal parts which are there in a collection.

Recommended Games
Definition of Equivalent Fractions
The fractions that represent the same value but look different(i.e different numerators or denominators) are called equivalent fractions. In other words, two or more fractions are said to be equivalent fractions if they are equal to the same fraction after we simplify them.
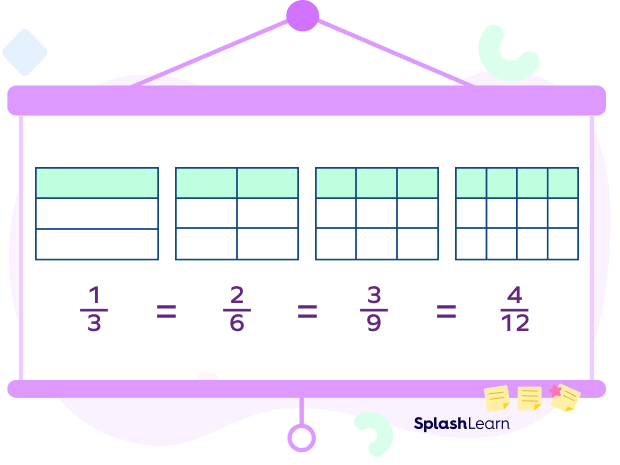
In the above image,
$\frac{1}{3}$, $\frac{2}{6}$, $\frac{3}{9}$ and $\frac{4}{12}$ seem to be different but they are equivalent fractions as on simplification, we get the fraction $\frac{1}{3}$.
Let us consider this through an example:

Ann and Eden bought a cake. They decided to share the cake. Ann had $\frac{4}{8}$ of the cake whereas Eden had $\frac{1}{2}$ of the cake. Did they divide the cake equally?
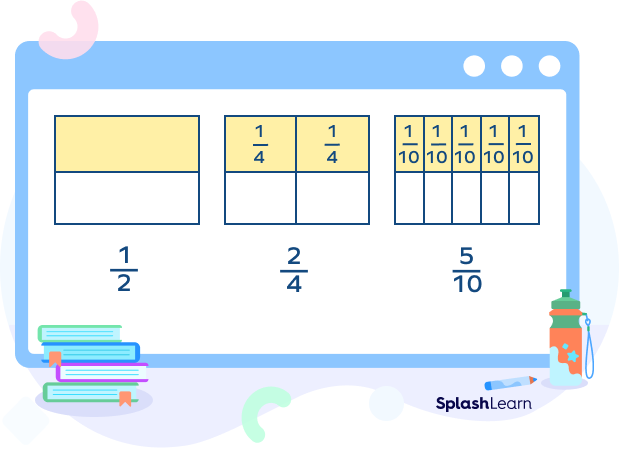
Yes; they did. Two fractions might look different but, upon simplification, have the same mathematical value and hence $\frac{4}{8}$ and $\frac{1}{2}$ are called equivalent fractions.
Consider, for example, $\frac{5}{10}$ and $\frac{2}{4}$ . They also seem different, but when we simplify them; they present the same value i.e, $\frac{1}{2}$.
Recommended Worksheets
How to Check Whether the Fractions are Equivalent or Not?
There are different ways to check whether the fractions are equivalent or not:
- Make the denominators the same
We can check whether the fractions are equivalent or not by making the denominators the same i.e., by finding the LCM of the denominators and then multiplying them with suitable numbers.
For example: In order to check whether $\frac{2}{8}$ and $\frac{3}{12}$ are equivalent or not, we will find the LCM of 8 and 12.
Step 1: Find LCM of denominators
LCM(8, 12) = 24
Step 2: Multiply by suitable numbers to make denominator the same = 24
$\frac{2 \times 3}{8 \times 3}$ = $\frac{6}{24}$ and $\frac{3 \times 2}{12 \times 2}$ = $\frac{6}{24}$
Since both the fractions came out to be $\frac{6}{24}$, so they are equivalent fractions.
- Finding the decimal form for both the fractions.
Decimal form of $\frac{2}{8}$ is 0.25.
Decimal form of $\frac{3}{12}$ is 0.25.
Since, the decimal form of both the fractions is 0.25, so they are equivalent fractions.
- Cross multiplication method
We will multiply the fractions. If the product comes out to be the same, the fractions are equivalent.
2 $\times$ 12 = 24 8 $\times$ 3 = 24
Since both the products are same, the fractions are equivalent.
- Visual Method
We can determine the equivalent fractions on identical shapes and check whether the shaded portions are equal or not.

In the above image, we see the shaded portions of both the circles depicts the same value. So, they are equivalent fractions.
Finding an Equivalent Fraction
To find equivalent fractions, we multiply or divide both the numerator and the denominator by the same number. There are two ways in which we can make equivalent fractions:
- Multiply the numerator and denominator by the same number
We can multiply the numerator and the denominator by the same number in order to find the equivalent fractions.
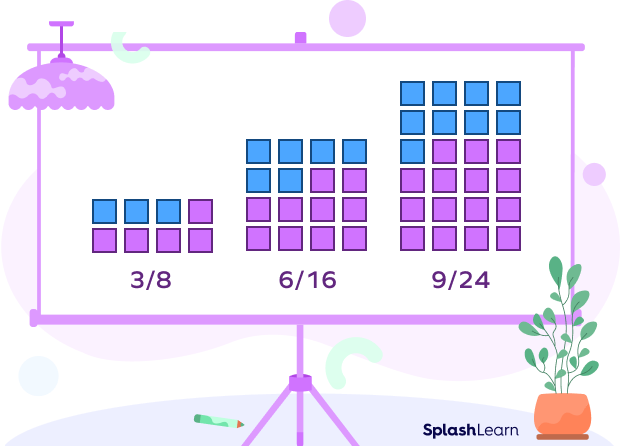
For example: We have to find two equivalent fractions for $\frac{3}{8}$.
Multiplying the numerator and denominator by 2.
$\frac{3 \times 2}{8 \times 2}$ = $\frac{6}{16}$
Multiplying the numerator and denominator by 3.
$\frac{3 \times 3}{8 \times 3}$ = $\frac{9}{24}$
The two equivalent fractions for $\frac{3}{8}$ are $\frac{6}{16}$ and $\frac{9}{24}$.
- Divide the numerator and denominator by the same number.
We can divide the numerator and the denominator by the same number in order to find equivalent fractions.
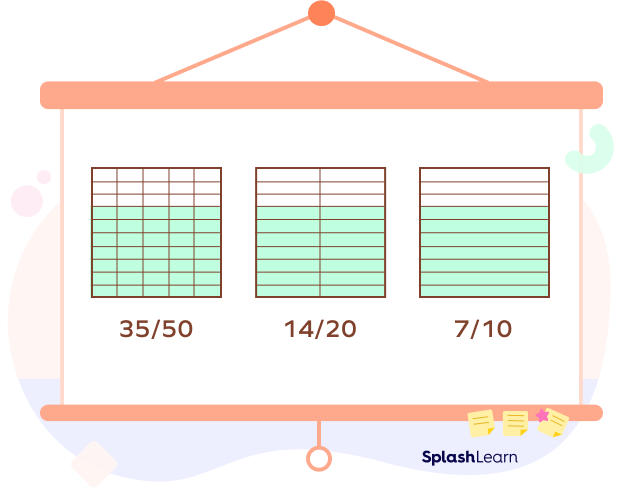
For example: To find equivalent fractions for $\frac{70}{100}$.
First find the common factors of 70 and 100.
The common factors of 70 and 100 are 2, 5 and 10.
Multiplying the numerator and denominator by 2.
$\frac{70 \div 2}{100 \div 2}$ = $\frac{35}{50}$
Multiplying the numerator and denominator by 5.
$\frac{70 \div 5}{100 \div 5}$ = $\frac{14}{20}$
Multiplying the numerator and denominator by 10.
$\frac{70 \div 10}{100 \div 10}$ = $\frac{7}{10}$
The equivalent fractions for $\frac{70}{100}$ are $\frac{35}{50}$ , $\frac{14}{20}$, and $\frac{7}{10}$.
Solved Examples
1. Check if $\frac{3}{9}$, $\frac{4}{12}$ and $\frac{5}{15}$ are equivalent fractions.
Upon simplifying $\frac{3}{9}$, we get $\frac{1}{3}$. Similarly, upon simplifying $\frac{4}{12}$, we get $\frac{1}{3}$. And, upon simplifying $\frac{5}{15}$ we again get the same value, $\frac{1}{3}$. As we get the same values after the simplification, these are equivalent fractions.
2. What will be the value of x if $\frac{2}{3}$ = $\frac{x}{12}$.
Since $\frac{2}{3}$ = $\frac{x}{12}$, it means we have multiplied the denominator by 4. So, we will multiply the numerator also by 4.
x = 2 $\times$ 4 = 8
3. Find three equivalent fractions for $\frac{2}{3}$.
Multiplying both numerator and denominator by 2, we get $\frac{2 \times 2}{3 \times 2}$ = $\frac{4}{6}$.
Multiplying both numerator and denominator by 3, we get $\frac{2 \times 3}{3 \times 3}$ = $\frac{6}{9}$.
Multiplying both numerator and denominator by 4, we get $\frac{2 \times 4}{3 \times 4}$ = $\frac{8}{12}$.
The three equivalent fractions for $\frac{2}{3}$ are $\frac{4}{6}$, $\frac{6}{9}$ and $\frac{8}{12}$.
Practice Problems
Equivalent Fractions
$\frac{12}{16}$ is an equivalent fraction of
On dividing both numerator and denominator of $\frac{12}{16}$ by 4, we get $\frac{3}{4}$.
What should be multiplied to the numerator and denominator of $\frac{2}{5}$ to make it equivalent to $\frac{8}{20}$?
2 $\times$ 4 = 8 and 5 $\times$ 4 = 20, so both numerator and denominator should be multiplied by 4.
Find equivalent fraction to $\frac{2}{3}$
On dividing both numerator and denominator of $\frac{60}{90}$ by 20, we get the fraction $\frac{2}{3}$.
Conclusion
Equivalent fractions have different face values, but upon simplifying them, they give the same numerical values. You can find these fractions by multiplying the denominator and numerator with the same number/value. Head to SplashLearn to learn about the equivalent fractions in a fun and easy way.
Frequently Asked Questions
How to figure out whether fractions are equivalent or not?
To determine whether fractions are equivalent or not, simplify the fractions to their lowest terms. If after simplification the fractions are the same, then they are equivalent if not then they are not equivalent.
How to find equivalent fractions to a given fraction?
We can either multiply or divide both the numerator and the denominator of the given fraction by the same number to generate equivalent fractions to the given fraction.
Why are equivalent fractions important?
Equivalent fractions help us in adding, subtracting, multiplying, dividing fractions, and also in comparing and ordering fractions which helps us solve many real-time problems.




































