What Is a Proper Fraction in Math?
A proper fraction is a fraction whose numerator is less than the denominator. A proper fraction always lies between 0 and 1 since the denominator is larger than the numerator.
Proper Fraction Examples: $\frac{1}{2},\; \frac{2}{5},\; \frac{3}{4},\; \frac{5}{7}$

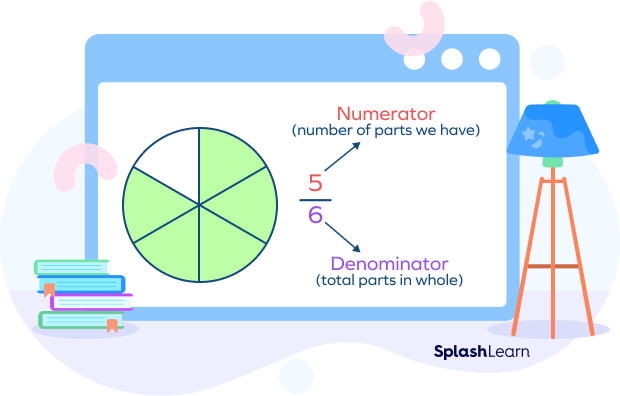
What does fraction mean in math? A fraction represents a part of a whole. A fraction has two parts. The number on the top of the line is called the numerator. It tells us how many equal parts of the whole or collection are taken. The number below the line is called the denominator.
Fractions are categorized on the basis of the value of the numerator and the denominator as:
- Proper Fractions: Numerator $\lt$ Denominator
- Improper Fractions: Numerator $\ge$ Denominator
Let’s learn about proper fractions in detail.
Definition of Proper Fraction
Fractions in which the numerator is less than the denominator are called proper fractions. The value of a proper fraction is always less than 1.
For example, $\frac{18}{20},\; \frac{19}{40},\; \frac{60}{80},\; \frac{1}{4}, \frac{1}{6}$, are proper fractions.

Recommended Games
Proper Fractions on a Number Line
A proper fraction has a value between 0 and 1. It is a fraction that lies between 0 and 1 on a number line.
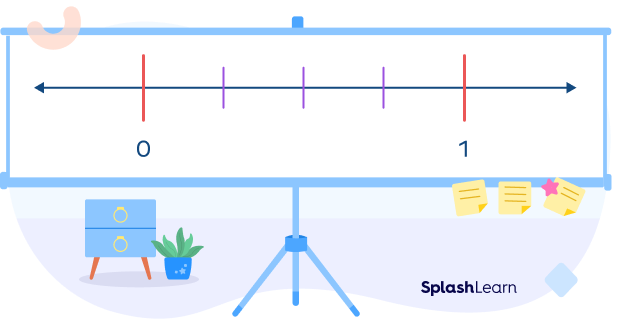
Example: Represent the proper fraction $\frac{1}{4}$ on a number line.
To represent a proper fraction on the number line, we first look at the denominator.
This number tells us the number of parts the interval between 0 and 1 is to be divided into.
Here, the denominator is 4. Thus, we divide the segment joining 0 and 1 into 4 equal parts.
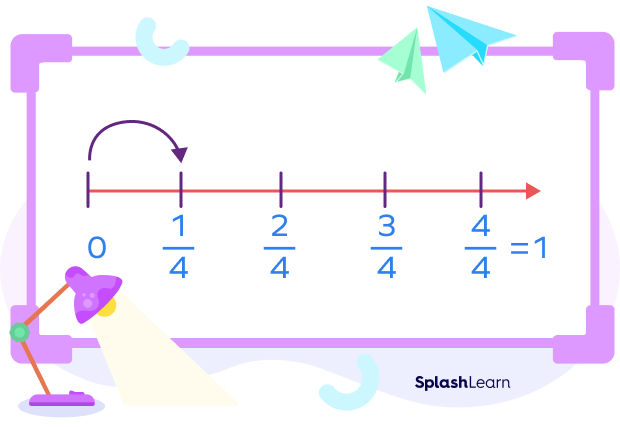
The numerator tells us where we place the dot or the mark to represent the given fraction. Here, the numerator is 1. Thus, we represent $\frac{1}{4}$ on the first marking.
Recommended Worksheets
Visualize Proper Fractions
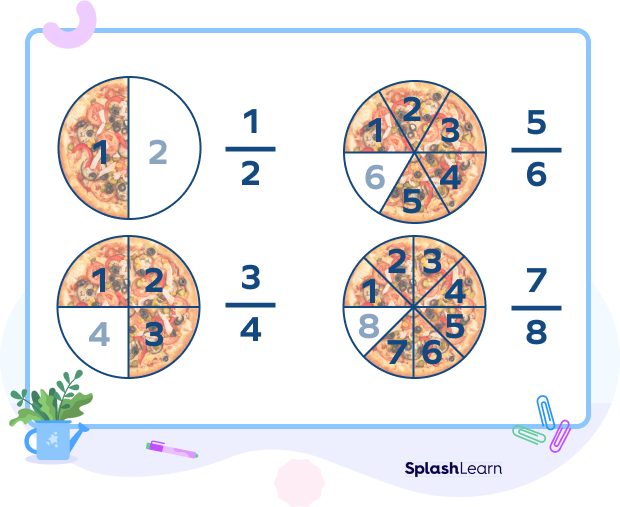
Suppose you cut a pizza in equal parts, you can express each slice in the form of a fraction.
If you divide it in two equal parts, each part represents “half” or the fraction $\frac{1}{2}$.
If you divide it in four equal parts, each part represents “a quarter” or the fraction $\frac{1}{4}$.
When we represent a proper fraction visually like this, notice that we never have enough slices to complete the whole pizza. Some slices are always missing.
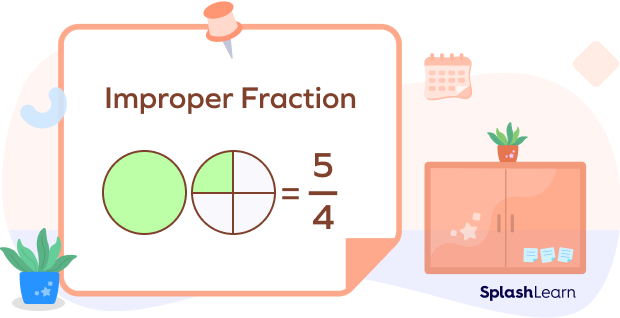
On the other hand, when we represent an improper fraction, we can always represent a whole and still some parts (slices) are left.
Adding Proper Fractions
We consider two cases when we add two or more proper fractions.
- Case 1: Denominators are the same.
- Case 2: Denominators are different
Case 1: Denominators Are Same
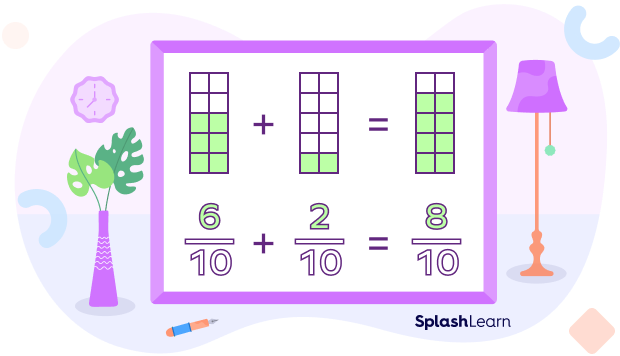
When the denominators of two or more fractions are the same, we call them like fractions. Adding proper fractions with the same denominator is simple.
If denominators are the same, we simply add the numerators by keeping the denominator as it is.
Example 1: $\frac{1}{4} + \frac{2}{4} = \frac{2 + 1}{4} = \frac{3}{4}$
Example 2: $\frac{6}{10} + \frac{2}{10} = \frac{6 + 2}{10} = \frac{8}{10}$
Case 2: Denominators Are Different
If denominators are different, we first take the LCM (Least Common Multiple) of the denominators and then rewrite the fractions as equivalent fractions using the LCM as the common denominator.
Once the denominators become the same, we add the numerators.
Example: $\frac{1}{2} + \frac{1}{4}$
Here, we will list the multiples of 2 and 4.
Multiples of 2: 2, 4, 6, 8, 10,…
Multiples of 4: 4, 8, 12, 16,…
4 is the Lowest Common Multiple.
LCM $(2,\; 4) = 4$
We need to find a number which when multiplied to the top and bottom of 12, we get the LCM (4) as the new denominator.
$\frac{1\times?}{2\times?} = \frac{?}{4}$
As $2\times2 = 4$ , we need to multiply the numerator and the denominator by 2.
$\frac{1\times2}{2\times2} = \frac{2}{4}$
Now we have, $\frac{2}{4} + \frac{1}{4} = \frac{3}{4}$
Subtracting Proper Fractions
Subtraction of proper fractions is similar to addition of proper fractions.
Case 1: If denominator is same, we simply find the difference between the numerators
For example: $\frac{5}{10} \;-\; \frac{3}{10} = \frac{5 \;-\; 3}{10} = \frac{2}{10}$
Case 2: If the denominators are not the same, we take the LCM of the denominators and when denominators become the same we find the difference between the numerators.
For example: subtract $\frac{6}{9} \;-\; \frac{2}{4}$
The LCM of 9 and 4 is 36.
Now, we multiply both the fractions with such a number (in this case, 4 and 9 respectively) so that the denominators become equal.
$\frac{6\times4}{9\times4} \;-\; \frac{2\times9}{4\times9} = \frac{24}{36} \;-\; \frac{18}{36} = \frac{24 \;-\; 18}{36} = \frac{6}{36} = \frac{1}{6}$
Multiplying Proper Fractions
Multiplication and division of proper fractions is easier compared to addition and subtraction.
We simply multiply the given numerators, then multiply the denominators, and finally reduce the resultant fraction.
Example: $\frac{3}{7}\times\frac{2}{4} = \frac{3\times2}{7\times4} = \frac{6}{28} = \frac{3}{14}$
Dividing Proper Fractions
To divide one fraction by another fraction, we multiply the fraction on the top (first fraction or the dividend) by the reciprocal of the fraction on the bottom (second fraction or the divisor).
Let’s take an example to understand the process of division.
Example: $\frac{3}{10} \div \frac{2}{3}$
Reciprocal of $\frac{2}{3} = \frac{3}{2}$
$\frac{3}{10}\div \frac{2}{3} = \frac{3}{10}\times\frac{3}{2} = \frac{9}{20}$
Proper Fraction and Improper Fraction
A proper fraction is a fraction whose numerator is smaller than its denominator.
$\frac{5}{12},\; \frac{2}{10},\; \frac{1}{2}$ are a few examples of proper fractions.
An improper fraction is a fraction whose numerator is equal to or greater than its denominator. $\frac{12}{5},\; \frac{10}{4},\; \frac{12}{11},\; \frac{5}{5}$ are a few examples of improper fractions.
Improper fractions are often expressed as a mixed number. A mixed number has a whole number part and a fractional part. The fractional part of a mixed fraction is always a proper fraction.
Example: $\frac{12}{5} = 2\frac{2}{5}$
Proper Fraction vs. Improper Fraction
| Proper Fraction | Improper Fraction |
|---|---|
| Numerator $\lt$ Denominator (Numerator is less than the denominator.) | Numerator $\ge$Denominator (Numerator is greater than or equal to the denominator.) |
| The value of the proper fraction is always between 0 and 1. | The value of the improper fraction is greater than or equal to 1. |
| Examples: $\frac{5}{6},\; \frac{2}{7},\; \frac{1}{2}$ | Examples: $\frac{12}{5},\; \frac{10}{9},\; \frac{12}{12}$ |
Improper Fractions to Proper Fractions
We cannot convert an improper fraction to a proper fraction. Proper fractions lie between 0 and 1. They do not have any whole number part. Improper fractions are greater than 1. They have a whole number part and some fractional part. Thus, there is no equivalence.
However, an improper fraction can be converted to a mixed fraction. A mixed fraction or a mixed number consists of a whole number and a proper fraction. Thus, note that we can basically convert an improper fraction to a mixed number.
Let us convert $\frac{25}{6}$ to mixed fraction.
Divide 25 by 6.
$25\div6 = 4\; R\; 1$
It means that the quotient is 4, with a remainder of 1.
Use the quotient = 4 as the whole number part of the mixed number, and place the remainder = 1 as the numerator over the original denominator.
$\frac{25}{6} = 4\frac{1}{6}$
Here, 4 is the whole number and $\frac{1}{6}$ is the proper fraction.
We can convert this mixed number back to the improper fraction form:
$4\frac{1}{6} = \frac{(6\times4) + 1}{6} = \frac{24 + 1}{6} = \frac{25}{6}$
How to Add a Mixed Fraction to a Proper Fraction
To add a mixed fraction to a proper fraction we convert the mixed fraction to an improper fraction. Then we add the two fractions in the usual way. After finding the answers we again convert the result into a mixed fraction.
Let us look at an example: $3\frac{1}{5} + \frac{1}{4}$
Convert mixed fraction into improper fraction.
$3\frac{1}{5} = \frac{16}{5}$
$\frac{16}{5} + \frac{1}{4} = \frac{16\times4}{5\times4} + \frac{1\times5}{4\times5}$ …since LCM$(4,\; 5) = 20$
$= \frac{64}{20} + \frac{5}{20}$
$= \frac{64 + 5}{20}$
$= \frac{69}{20}$
Now, we also can convert improper fraction into mixed fraction which will be $3\frac{9}{20}$.
Facts about Proper Fractions
- The word fraction is acquired from the Latin word “fractus,” which implies “broken.”
- Every whole number can be written as a fraction. For example, 2 can be written as $\frac{2}{1}$.
- A proper fraction is one where the numerator is less than the denominator.
- The NUMERATOR tells how many pieces of the whole the fraction represents.
- The DENOMINATOR tells how many equal pieces the whole is divided into.
- Proper fractions are used with whole numbers to denote a sum that is greater than 1.
Conclusion
In this article, we have learned about proper fractions, their addition, multiplication, subtraction, and division. Let’s solve some examples to understand the concept better.
Solved Examples on Proper Fractions
1. Identify whether the following are proper fractions.
a) $\frac{10}{12}$ b) $\frac{15}{11}$ c) $\frac{18}{18}$
Solution:
a) $\frac{10}{12}$ is a proper fraction as the numerator is less than the denominator.
b) $\frac{15}{11}$ is not a proper fraction as the numerator is greater than the denominator. It is an improper fraction.
c) $\frac{18}{18}$ is not a proper fraction because in this case the numerator is equal to the denominator. It is an improper fraction.
2. Add the proper fractions: $\frac{10}{20} + \frac{15}{20}$.
Solution:
If denominators are the same, we simply add the numerators.
$\frac{10}{20} + \frac{15}{20} = \frac{10 + 15}{20} = \frac{25}{20}$
It can also be reduce or simplified further as $\frac{25\div5}{20\div5} = \frac{5}{4}$
Therefore, $\frac{10}{20} + \frac{15}{20} = \frac{25}{20} = \frac{5}{4}$
3. Solve $\frac{6}{20}\div \frac{1}{2}$ .
Solution:
Multiply the first fraction by the reciprocal of the second fraction.
$\frac{6}{20}\div\frac{1}{2} = \frac{6}{20}\times \frac{2}{1} = \frac{6\times2}{20\times1} = \frac{12}{20}$
$\frac{12}{20}$ can be further reduced as $\frac{12\div4}{20\div4} = \frac{3}{5}$
Therefore, $\frac{6}{20}\div\frac{1}{2} = \frac{3}{5}$
4. Subtract $\frac{2}{5} \;-\; \frac{1}{4}$.
Solution:
Here, the denominators are not the same, so we take the LCM of the denominators and when denominators become the same we find the difference between the numerators.
The LCM of 5 and 4 is 20.
Now, we multiply both the fractions with such a number (in this case, 5 and 4 respectively) so that the denominators become equal.
$\frac{2\times4}{5\times4} \;-\; \frac{1\times5}{4\times5} = \frac{8}{20} \;-\; \frac{5}{20}$
$= \frac{8 \;-\; 5}{20}$
$= \frac{3}{20}$
Therefore, $\frac{2}{5} \;-\; \frac{1}{4} = \frac{3}{20}$
5. Add $2\frac{3}{6} + \frac{3}{8}$.
Solution:
Here, we first convert a mixed fraction into an improper fraction.
$2\frac{3}{6} = \frac{15}{6}$
Now, we add the two fractions $\frac{15}{6}$ and $\frac{3}{8}$.
$\frac{15}{6} + \frac{3}{8} = \frac{15\times4}{6\times4} + \frac{3\times3}{8\times3}$
$= \frac{60}{24} + \frac{9}{24}$
$= \frac{69}{24}$
This can be further reduced as $\frac{69\div3}{24\div3} = \frac{23}{8}$
Expressing it as mixed fraction $\frac{23}{8} = 2\frac{7}{8}$
Therefore, $2\frac{3}{6} + \frac{3}{8} = 2\frac{7}{8}$
Practice Problems on Proper Fractions
Proper Fraction - Definition, Examples, Facts, FAQs
The fraction representation of the shaded portion is _________.

The whole is divided into 2 parts. So the shaded part is $\frac{1}{2}$ .
Which of the following is a proper fraction ?
A fraction is called a proper fraction if its numerator is less than its denominator. Thus, $\frac{7}{9}$ is a proper fraction.
Which of the following is NOT a proper fraction ?
A fraction is called a proper fraction if its numerator is less than its denominator. An improper fraction is a fraction whose numerator is equal to or greater than its denominator. As 11 is greater than $3,\; \frac{11}{3}$ is an improper fraction.
$\frac{1}{3} + \frac{2}{3} =$ _______.
If denominators are the same, we simply add the numerators by keeping the denominator as it is. Thus, $\frac{1}{3} + \frac{2}{3} = \frac{1 + 2}{3} = \frac{3}{3} = 1$
Find the sum of fractions.
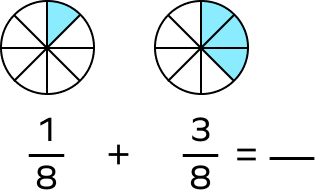
$\frac{1}{8} + \frac{3}{8} = \frac{4}{8}$
Frequently Asked Questions on Proper Fractions
Is 1 a fraction?
When numerator equals denominator, a fraction becomes 1. It is considered as an improper fraction.
What are mixed fractions?
Mixed fractions consist of a whole number and a proper fraction. Since mixed fractions are combinations of whole numbers and a fraction, mixed fractions are always greater than 1.
Why is it preferable to simplify fractions down to their lowest possible form?
We simplify fractions because it is always easy to work or calculate when the fractions are in the simplest form. Simplified or lowest form or reduced form of a fraction makes the calculation easier.
What are like and unlike fractions?
Fractions with the same denominators are called “like” fractions. For example, $\frac{2}{4}$ and $\frac{3}{4}$.Fractions with different denominators are called “unlike” fractions. For example, $\frac{1}{2}$ and $\frac{2}{3}$.
Can a proper fraction be negative ?
Yes, the proper fraction can be negative or positive. A negative proper fraction will have a negative sign either in numerator or denominator. For example, $\frac{-3}{4}$.
Why is an improper to proper fraction conversion not possible?
A proper fraction is always less than 1, while an improper fraction is always greater than 1. Thus, we cannot express a proper fraction in the form of an improper fraction. Similarly, mixed fraction to proper fraction conversion is also not possible. However, we can convert an improper fraction to a mixed number and vice-versa.
Is $\frac{4}{3}$ a proper fraction?
$\frac{4}{3}$ is not a proper fraction. The numerator is greater than the denominator. Thus, $\frac{4}{3}$ is an improper fraction.




































